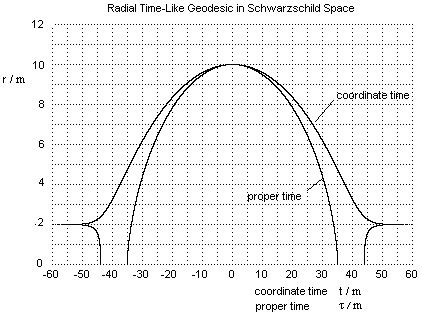
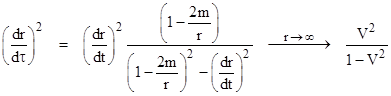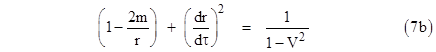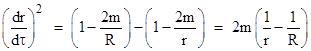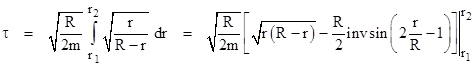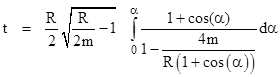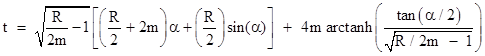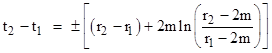定积分和不定积分的区别
这两者是从不同角度定义的不同概念。
不定积分是一个函数的全体原函数,是一个函数族(函数的集合);
定积分是与函数有关的一个和式的极限,是一个实数。
从概念而言,这两者是完全不同的、毫无关系的,或者说是风马牛不相及的。
但是牛顿-莱布尼兹公式却把它们联系起来,这就是这两位先驱者的伟大之处,虽然在今人看起来并没有多少深奥,倒反而有人会把这两个概念混淆在一起。如果当初这两个概念也那么容易相混的话,大概等不到牛顿出生,微积分早被创立了。
牛顿-莱布尼兹公式告诉我们,定积分那个极限,等于被积函数的原函数在积分区间右端点的值减去左端点的值,定积分也就与原函数有了联系,定积分之所以叫定积分大概也是因为这个原因。但是取这个名也有副作用,因为不定积分比定积分只多了一个“不”字,一些人就认为它们是一样的或者是稍有区别的,这大概也是今天这个问题被提出的原因。
建议学习高等数学的同学们,不要问不定积分与定积分有什么区别,而是把它们作为两个完全不同的概念分别学习好,再也不要搞混在一起。
不定积分是一个函数的全体原函数,是一个函数族(函数的集合);
定积分是与函数有关的一个和式的极限,是一个实数。
从概念而言,这两者是完全不同的、毫无关系的,或者说是风马牛不相及的。
但是牛顿-莱布尼兹公式却把它们联系起来,这就是这两位先驱者的伟大之处,虽然在今人看起来并没有多少深奥,倒反而有人会把这两个概念混淆在一起。如果当初这两个概念也那么容易相混的话,大概等不到牛顿出生,微积分早被创立了。
牛顿-莱布尼兹公式告诉我们,定积分那个极限,等于被积函数的原函数在积分区间右端点的值减去左端点的值,定积分也就与原函数有了联系,定积分之所以叫定积分大概也是因为这个原因。但是取这个名也有副作用,因为不定积分比定积分只多了一个“不”字,一些人就认为它们是一样的或者是稍有区别的,这大概也是今天这个问题被提出的原因。
建议学习高等数学的同学们,不要问不定积分与定积分有什么区别,而是把它们作为两个完全不同的概念分别学习好,再也不要搞混在一起。
曲线积分的物理意义 [引用和转载请标明本文 CU blog 出处] 定积分的求解---牛顿.拉布尼茨公式有什么几何意义? 简单的说,因为 F(b)-F(a)在几何上是 f(x) 的原函数 F(x)在 y 轴上的线段长度,那么这个长度如何表示呢? F(b)-F(a)可以写成在区间[a,b]上面的累 加 Sigma(F'(x)*delta(x)),那么这个 Sigma 就是 f(x)的定积分了。反向构造的方法联系了不定积分和 定积分(图 1)。 太抽象了,举个有物理含义的例子(图 2)。 1. 假设 x/y 平面是一个力场,一个质点在立场中受力,它受的力在 x 轴方向方向的投影值,恰好等于它 的 y 坐标(力的正负代表方向)。 2.那么这个例子沿着曲线 y^2=x,从(1,-1)移动到(1,1),立场对它作了多少功? 我们可以画出一个图形,粒子在 y 的负半平面受的力总是向左的(负号),在 y 的正半平面受的力总 是向右的,所以立场一直在 x 轴方向对例子做正的功。做功的积分式子分为两个部分,(1,-1)到(0,0)的过 程是 S[x,1,0],dx 是负数,力 y=x^0.5 也是负数,负负得正。所以做的总功=2*S[x,0,1](x^0.5), 这个解求很简单了。那么如果立场还有一个 y 方向呢? 叠加的结果就是 2*S[x,0,1]+S[y,-1,1],写成积 分式子,就是对于坐标的曲线积分。
格林公式(图 3)的意义在于: 一维的定积分通过牛顿---莱布尼茨公式得到了完满的解决,等于不定积分原函数的两个取值之差。 那么格林公式的意义呢? 曲线积分,分成 dx 和 dy 的两部分分别证明。考虑凸面曲线的情况,因为其他情 况可以分解为若干个凸面曲线的情况。例如要证明格林公式中关于 dy 的部分,就可以看作很多条平行于 x 轴的线穿过被积分的曲线,其中每一条直线和曲线交与两点,靠近 y 轴左半平面的点记做 Q1,靠近 y 轴 右半平面的点记做 Q2,那么根据曲线积分的正向定义,逆时针方向,Q1 点的微元 dy 是正的,Q2 点的 微元 dy 是负的。然后微元的和就是 Q1*dy+Q2*(-dy)=(Q1-Q2)dy。好了,Q1-Q2 又是多少呢? 由牛 顿莱布尼茨公式得到它是 Q2-Q1 这条线段上 Q'(x)的积分和。那么积分和的和就是一个 2 重积分。 用一个黎曼球面我们把|z|从 0 到无穷大的所有的矢量影射到了一个南北极的球面上面(彩图右上), 无穷的数域变成了有穷的数域。微分方程变成指数方程,纯为粉方程类似线形代数的方程组由通解和特解
组成解系;指数变成拉伸和旋转,平面几何的问题变成解析几何的问题。举个例子,如何判断两条直线是 否垂直,那么 z1(角度 Theta1)和 z2(角度 Theta2)互相垂直相当于 z1 和 z2 之间的夹角=正负 90 度。 由于复数的乘法包含了角度的相加,那么 z2 的共轭矢量角度就是-Theta2。它们两个相乘的结果矢量角就 是 Theta1-Theta2,如果这个角度是 90 度,那么 z1*z2'就应该是一个纯虚数,反之,z1*z2'是个纯虚 数,就说明 z1 和 z2 垂直。所谓的"虚数"并不是不存在,而是它的值在实数轴 x 上面的投影总是 0。那么 写出来就是a+bi与c+di正交的充要条件就是ac+bd=0----看起来像是线形代数里面的[a,b]与[c,d] 互 相正交的充要条件是矢量点乘=0。复数,确实是用线形代数的方式在研究高等数学,把函数的研究统一到 了解析几何。这里,代数和几何没有区别。 再举一个例子,平面几何的命题(图 4):一个三角形 AB=AC,AB 上有线段 mn,AC 上有线段 jk, 长度 mn=长度 jk,证明 mj 的中点 x 和 nk 的中点 y,连线垂直于 BC。这道题如果用初等数学平面几何 的性质,脑袋破了都很难证明,因为平面几何的定理是用语言表述的某种性质,证明的过程也是和人对图
形的感性认识密切相关,例如垂直平分线,等腰三角形,这些自然语言的概念用起来太费劲,而且必须结 合图形本身来使用。OK,用复数来证明,使用一个形式语言的演算系统: 1. 假设 AB 是实数轴,AC 是和 AB 夹角为 a 的向量,那么假设等腰边长为 l ,那么
AB=l,AC=l(cosa+isina),BC=AC-BC=l(cosa-1 +isina)。 2. 假设 mn 和 jk 的长度为 r,m=M+0i,j=M(cosa+isina),那么 n=M+r,k=(M+r)(cosa+isina)。 3. mj 的中点就是 d1=(m+j)/2,nk 的中点就是 d2=(n+k)/2,两点之间的连线的方向矢量 f1=d2-d1=(n+k-m-j)/2 4. BC 的共轭矢量 f2=l(cosa-1-isina) 5. f1*f2,去掉实系数=(cosa+1+isina)(cosa-1-isina),实部=cosa^2-1+sina^2=0,所以是个纯 虚书,根据上例的结果,f1 和 f2 垂直,证毕。 再举一个证明题:平行四边形对角线的平方和=相邻对角线平方和的两倍。那么设四边形的两条边 是矢量 z1 和 z2 ,那么|z1+z2|^2+|z1- z2|^2=(z1+z2)(z1'+z2')+(z1-z2)(z1'-z2')=2z1z1'+2z2z2'=2(|z1|^2+|z2|^2)得证。复数的函 数(复变函数)往往具有对称性的性质。如果 f(z)=a0+a1z^1+...+anz^n=X+Yi,那么可以证明, f(z')=X- Yi。有什么作用吗? 如果函数 f(z)=0 有解 a+bi,那么 a-bi 也是解(显然因为 X=Y=0)。复数 更重要的特征是矢量的方向性。一个直线过 z1,z2 的端点,那么方向就是 M(z2-z1),直线方程就可以写 成点法式: z1+M(z2-z1)=Mz2+(1-M)z1。 朱力斯·华纳有一幅很著名的画叫做"神秘的岛屿"(彩图左上),这个画的内容看起来是个探险的小 岛,但是把一个圆柱形的镜面放到画的中央,人们惊奇的发现其实这是作者的自画像。如果这幅洋洋洒洒 的油画是代表了实数的问题,那些无穷无尽的无比复杂的现实问题,那么这个圆柱形的镜子就是"复数"这 样一个发明,它把无穷复杂的问题变成了有穷范围内能表达的问题。由于一一映射的存在,实数域难以解
决的问题通过映射和等效,在复数域通常能得到简单的解答,再映射回实数域,便是问题的解。例如著名 的莫比乌斯变换(彩图右下)。
需要很好的考虑几个问题: 1. 我们在把可积函数变成傅立叶级数的时候,曾经强调过,每个分量之间由于是三角函数族的成员,所以 构成正交关系,所以显然,分量之间没有重叠,展开式显然唯一。那么对于泰勒级数和复分析当中的洛朗 级数而言,函数的幂级数展开式是否是唯一的? 我们主要到没有任何条件限制规定展开分量之间必须构成 正交关系。正交性并不必要,基不需要正交性。 z 和 z^2 线性无关(注意是“线性”)因为不存在 c1 和 c2\in R,使得 c1*z + c2*z^2=0, 对于所有的 z 属于 R 都成立(z 是变量,可以任意取)。严格的说,“幂分量” 不需正交,仅要线性无关即可。反证法,我们假设幂级数的分量之间是线形相关的,也就是存在常数 k1-kn 使得(k1(1 是角标))k1x+k2x^2+k3x^3+...+knx^n =0。我们又知道前面这个方程,在复数域中仅 有 n 个解,即 0 点仅有 n 个。故只有 k1=k2=....=kn 左端才恒为 0(对于任意的 z),这就是线性无关的 条件,n 任意个,即无穷个 x^i 都线性无关。当然这里线性空间是一个函数空间,其实 x,x^2,...构成其 一个基----所以 k1-kn 都是 0, {z^n}构成的分量,是个线性无关的集合(两两之间)。 2. 为什么洛朗级数(彩图红色圆环)里面会有复数次幂? 我们去掉不解析的点,就得到了一些列圆环,这个 圆环上作闭合路径包围一定的面积,就是里外两条曲线,外围曲线就是洛朗技术的 n>=-1 的幂次项,内 围曲线是反方向的环绕无穷原点(很奇怪吗? 只要把 z 平面映射到黎曼球面上,就会得到这个结论!),是一 个负数的积分结果,它的收敛半径相反,我们把 z 用 z 的倒数来代替,就得到了和前半部分几乎一样的表 达式。所以洛朗级数的形式是 Sigma 从 n=负无穷到正无穷的形式(完备)。特别的,如果圆环是圆饼,那 么内环等于是不存在或者收缩到了一个点,也就是 n<-1 的那些负数次幂不存在了,函数解析,得到洛朗 级数等于泰勒级数的结论。实变函数可以展开成泰勒级数----本质的意义不在于泰勒级数的导数项,而是 在于,函数可以展开成自变量所表达的一个幂级数求和表达式,这个有点像离散结构里面的 P 问题。那么 对于复数,因为解释函数的方向导数有无数个,所以无法直接表示成泰勒级数,但是仍然可以写成幂级数 求和的形式----洛朗级数,同时,可以把泰勒级数看成洛朗级数在实轴方向上投影的特例。当然,这个时 候的幂级数系数不能再用导数来求了(切线逼近法),而是使用一个积分。Taylor 级数可以看作 Lorent 级 数的特例。泰勒级数有个收敛域(x-x0,x+x0)和收敛条件 x 附近连续且可导。我们放到复数平面上来,收 敛域就是一个圆,在 x 点处解析。但是如果不满足解析条件呢? 对于一个复变量函数 f(z)来说,如果它在 某点是全纯的(解析的),则它一定有 Taylor 级数, 复平面的点和黎曼圆的点一一对应,所以所有的直线在无穷远处必定相交,哪怕是平行线----这就是 黎曼几何不同于欧式几何的一个地方。无穷远的点集被映射成为 N 点--->于是留数基本定理,所有奇异点 的留数和=0 就很好理解了: 流体从各个有限奇异点流出,汇聚到无穷远的奇异点,流入流出的总和=0。 同理,如果黑洞是一个奇异点,那么当黑洞需要喷发的时候,喷发的方向显然是阻力小的方向,和黑洞 周围的圆盘垂直的法向量。为什么复变函数里面会有那么怪异的柯西积分公式? 实际上还是从格林公式推 导出来的,解析函数对于某点的围线积分等于围绕 z0 点本身的无穷小圆的积分,这个性质说明了解析函 数的 2 维积分中值定理: f(z)可以从围线的积分中值来求,反过来,一个积分可以看成是 f(z)的洛朗级数 展开的-1 次项,于是 1 元积分学当中的许多问题就借助 2 元复变函数得以解决了。 格林公式是把 1 维的围线积分和 2 重积分联系起来了,而复数则推广了,一维的围线积分(被积函数 有不可导点)还可以等价于被积函数本身的取值。这真是一个简单而且美的结论----f(z)*2Pi*i 的取值等于 围绕着 z,f(w)/(z-w)做一圈封闭的曲线积分----当然和曲线的形状无关。f(z)和非 z 点的 f(w)被这个方 程式统一了起来,多么奇妙的一件事情。如果把 z 看成圆点(黑洞),那么就是圆点这个黑洞的能量可以通 过围绕这个黑洞的一个曲线上的矢量积分来判定,黑洞变得可以测量了。另一方面,这个方程给出了解析 的函数,各个点之间的某种相关性。一个点可以用其他的点集的某种积分来表示。
(Abel 整理于网络,非原创)
化学基本概念反映化学物质的本质属性,是化学的基础。明确概念的内涵与外延,是正确把握知识的要素,也是正确判断和推理的基础,因此在概念的教学中,让学生掌握、运用概念,尤为重要。同位素、同素异形体、同系物、同分异构体和同一种物质等化学中几个经常用到的概念,也是一些同学经常混淆的概念,下面就这几个概念的区别加以详细的说明。
对于同位素、同素异形体、同系物和同分异构体这四个概念,学习时应着重从其定义、对象、化学式、结构和性质等方面进行比较,抓住各自的不同点,从而理解和掌握。这几个概念都表明了事物之间的关系,下表列出了比较了它们的异同:
同位素
|
同素异形体
|
同系物
|
同分异构体
| |
定义
|
质子数相同,中子数不同的原子(核素)
|
由同一种元素组成的不同单质
|
结构相似,分子组成相差一个或若干个CH2基团的物质
|
分子式相同,结构不同的化合物
|
对象
|
原子
|
单质
|
化合物
|
化合物
|
化学式
|
元素符号表示不同,如、、
|
元素符号表示相同,分子式可以不同,如O2和O3
|
不同
|
相同
|
结构
|
电子层结构相同,原子核结构不同
|
单质的组成或结构不同
|
相似
|
不同
|
性质
|
物理性质不同,化学性质相同
|
物理性质不同,化学性质相同
|
物理性质不同,化学性质相似
|
物理性质不同,化学性质不一定相同
|
说明:
1、同位素的对象是原子,在元素周期表上占有同一位置,化学性质基本相同,但原子质量或质量数不同,从而其质谱行为、放射性转变和物理性质(例如在气态下的扩散本领)有所差异。
2、同素异形体的对象是单质,同素异形体的组成元素相同,结构不同,物理性质差异较大,化学性质有相似性,但也有差异。如金刚石和石墨的导电性、硬度均不同,虽都能与氧气反应生成CO2,由于反应的热效应不同,二者的稳定性不同(石墨比金刚石能量低,石墨比金刚石稳定)。
同素异形体的形成方式有三种:
(1)组成分子的原子数目不同,例如: O2和O3 。
(2)晶格中原子的排列方式不同,例如:金刚石和石墨。
(3)晶格中分子排列的方式不同,例如:正交硫和单斜硫(高中不要求此种)。
(2)晶格中原子的排列方式不同,例如:金刚石和石墨。
(3)晶格中分子排列的方式不同,例如:正交硫和单斜硫(高中不要求此种)。
注意:同素异形体指的是由同种元素形成的结构不同的单质,如H2和D2的结构相同,不属于同素异形体。
3、同系物的对象是有机化合物,属于同系物的有机物必须结构相似,在有机物的分类中,属于同一类物质,通式相同,化学性质相似,差异是分子式不同,相对分子质量不同,在组成上相差一个或若干个CH2原子团,相对分子质量相差14的整数倍,如分子中含碳原子数不同的烷烃之间就属于同系物。
(1)结构相似指的是组成元素相同,官能团的类别、官能团的数目及连接方式均相同。结构相似不一定是完全相同,如CH3CH2CH3和(CH3)4C,前者无支链,后者有支链,但二者仍为同系物。
(2)通式相同,但通式相同不一定是同系物。例如:乙醇与乙醚它们的通式都是CnH2n+2O,但他们官能团类别不同,不是同系物。又如:乙烯与环丁烷,它们的通式都是CnH2n,但不是同系物。
(3) 在分子组成上必须相差一个或若干个CH2原子团。但分子组成上相差一个或若干个CH2原子团的物质却不一定是同系物,如CH3CH2Br和CH3CH2CH2Cl都是卤代烃,且组成相差一个CH2原子团,但二者不是同系物。
(4)同系物具有相似的化学性质,物理性质有一定的递变规律,如随碳原子个数的增多,同系物的熔、沸点逐渐升高;如果碳原子个数相同,则有支链的熔、沸点低,且支链越对称,熔、沸点越低。如沸点:正戊烷>异戊烷>新戊烷。同系物的密度一般随着碳原子个数的增多而增大。
4、同分异构体的对象是化合物,属于同分异构体的物质必须化学式相同,结构不同,因而性质不同。具有“五同一异”,即同分子式、同最简式、同元素、同相对原子式量、同质量分数、结构不同。属于同分异构体的物质可以是有机物,如正丁烷和异丁烷;可以是有机物和无机物,如氰酸铵和尿素;也可以是无机物,如[Pu(H2O)4]Cl3和[Pu(H2O)2Cl2]·2H2O·Cl。
在有机物中,很多物质都存在同分异构体,中学阶段涉及的同分异构体常见的有以下几类:
(1)碳链异构:指碳原子之间连接成不同的链状或环状结构而造成的异构。如C5H12有三种同分异构体,即正戊烷、异戊烷和新戊烷。
(2)位置异构(官能团位置异构):指官能团或取代基在在碳链上的位置不同而造成的异构。如1—丁烯与2—丁烯、1—丙醇与2—丙醇、邻二甲苯与间二甲苯及对二甲苯。
(3)类别异构(又称官能团异构):指官能团不同而造成的异构,如1—丁炔与1,3—丁二烯、丙烯与环丙烷、乙醇与甲醚、丙醛与丙酮、乙酸与甲酸甲酯、葡萄糖与果糖、蔗糖与麦芽糖等。
(4)其他异构方式:如顺反异构、对映异构(也叫做镜像异构或手性异构)等,在中学阶段的信息题中屡有涉及。
各类有机物类别异构体情况:
⑴ CnH2n+2:只能是烷烃,而且只有碳链异构。如CH3(CH2)3CH3、CH3CH(CH3)CH2CH3、C(CH3)4
⑵ CnH2n:单烯烃、环烷烃。
如CH2=CHCH2CH3、CH3CH=CHCH3、CH2=C(CH3)2、 、
⑶ CnH2n-2:炔烃、二烯烃、环烯烃。如:CH≡CCH2CH3、CH3C≡CCH3、CH2=CHCH=CH2、
⑷ CnH2n-6:芳香烃(苯及其同系物)。如: 、 、
⑸ CnH2n+2O:饱和脂肪醇、醚。如:CH3CH2CH2OH、CH3CH(OH)CH3、CH3OCH2CH3
⑹ CnH2nO:醛、酮、环醚、环醇、烯基醇。如:CH3CH2CHO、CH3COCH3、CH2=CHCH2OH、
、 、
⑺ CnH2nO2:羧酸、酯、羟醛、羟基酮。如:CH3CH2COOH、CH3COOCH3、HCOOCH2CH3、
HOCH2CH2CHO、CH3CH(OH)CHO、CH3COCH2OH
⑻ CnH2n+1NO2:硝基烷、氨基酸。如:CH3CH2NO2、H2NCH2COOH
⑼ Cn(H2O)m:糖类。如: C6H12O6:CH2OH(CHOH)4CHO、CH2OH(CHOH)3COCH2OH
C12H22O11:蔗糖、麦芽糖。
例1、下列各组物质中,两者互为同分异构体的是( )。
①CuSO4?3H2O和CuSO4?5H2O ②NH4CNO和CO(NH2)2
③ C2H5NO2和NH2CH2COOH
④[Pu(H2O)4]Cl3和[Pu(H2O)2Cl2] ?2H2O?Cl
A、①②③ B、②③④ C、②③ D、③④
解析:同分异构体是分子式相同,但结构不同。CuSO4?3H2O和CuSO4?5H2O组成就不同,不是同分异构体;NH4CNO和CO(NH2)2分子式相同,二者结构不同,互为同分异构体;C2H5NO2和NH2CH2COOH,前者是硝基化合物,后者是氨基酸,分子式相同,属于类别异构;[Pu(H2O)4]Cl3和[Pu(H2O)2Cl2] ?2H2O?Cl,前者表示四个水分子直接和Pu相结合,后者中是两分子的水和两个氯离子与Pu相结合,所以结构不同,互为同分异构体。正确选项为B。
例2、下列各组物质,其中属于同系物的是( )。
(1)乙烯和苯乙烯 (2)丙烯酸和油酸 (3)乙醇和丙二醇
(4)丁二烯与异戊二烯 (5)蔗糖与麦芽糖
A.(1)(2)(3)(4) B.(2)(4)
C.(1)(2)(4)(5) D.(1)(2)(4)
解析:同系物是指结构相似,即组成元素相同,官能团种类、个数相同,在分子组成上相差一个或若干个
CH2原子团,即分子组成通式相同的物质。乙烯和苯乙烯,后者含有苯环而前者没有;丙烯酸和油酸含有的官能
团都是双键和羧基,而且数目相同所以是同系物;乙醇和丙二醇官能团的数目不同;丁二烯与异戊二烯都是共
轭二烯烃,是同系物;蔗糖和麦芽糖是同分异构体而不是同系物。正确选项为B。
例3、有下列各组微粒或物质:
CH3
A、O2和O3 B、C和C C、CH3CH2CH2CH3和 CH3CH2CHCH3
H Cl CH3
D、Cl—C—Cl和Cl—C—H E、CH3CH2CH2CH3和CH3—CH—CH3
H H
(1) 组两种微粒互为同位素;
(2) 组两种物质互为同素异形体;
(3) 组两种物质属于同系物;
(4) 组两物质互为同分异构体;
(5) 组两物质是同一物质。
解析:这道题主要是对几个带“同字”概念的考查及识别判断能力。A项为都由氧元素形成的结构不同的单质,为同素异形体。B项为质子数相同,中子数不同的原子,属于同位素。C项均为烷烃结构,分子组成上相差一个CH2原子团,属于同系物。D项均为甲烷的取代产物,因而是立体结构,是同种物质。D项的分子式相同,结构不同(碳链异构),是同分异构体。
正确选项为:(1)B (2)A (3)C (4)E (5)D
例4.如果定义有机物的同系列是一系列结构简式符合: (其中n=0、1、2、3……)的化合物。式中A、B是任意一种基团(或氢原子),w为2价的有机基团,又称为该同系列的系差。同系列化合物的性质往往呈现规律性变化。下列四组化合物中,不可称为同系列的是:
A.CH3CH2CH2CH3 CH3CH2CH2CH2CH3 CH3CH2CH2CH2CH2CH3
B.CH3CH=CHCHO CH3CH=CHCH=CHCHO CH3(CH=CH)3CHO
C.CH3CH2CH3 CH3CHClCH2CH3 CH3CHClCH2CHClCH3
D.ClCH2CHClCCl3 ClCH2CHClCH2CHClCCl3 ClCH2CHClCH2CHClCH2CHClCCl3
解析:此题是95年全国高考题,也是一个信息题,信息中给出了一个新的概念同系列。在课堂上我们学习过同系物这一概念。这就形成了两个非常相近的概念,需要我们在理解新信息的基础上,进行对比、辨析,然后运用解题。同系物是指结构相似,在分子组成上相差一个或若干个CH2原子团的物质。而同系列是指结构相似,在结构上相差一个或若干个重复结构单元的物质。据此可迅速作出判断,正确选项为C。
A.CH3CH2CH2CH3 CH3CH2CH2CH2CH3 CH3CH2CH2CH2CH2CH3
B.CH3CH=CHCHO CH3CH=CHCH=CHCHO CH3(CH=CH)3CHO
C.CH3CH2CH3 CH3CHClCH2CH3 CH3CHClCH2CHClCH3
D.ClCH2CHClCCl3 ClCH2CHClCH2CHClCCl3 ClCH2CHClCH2CHClCH2CHClCCl3
解析:此题是95年全国高考题,也是一个信息题,信息中给出了一个新的概念同系列。在课堂上我们学习过同系物这一概念。这就形成了两个非常相近的概念,需要我们在理解新信息的基础上,进行对比、辨析,然后运用解题。同系物是指结构相似,在分子组成上相差一个或若干个CH2原子团的物质。而同系列是指结构相似,在结构上相差一个或若干个重复结构单元的物质。据此可迅速作出判断,正确选项为C。
练习:
1.在热核反应中没有中子辐射,作为能源时不会污染环境。月球上的储量足够人类使用1000年,地球上含量很少。和两者互为( )
A.同素异形体 B.同位素 C.同系物 D.同分异构体
解析:和的质子数相同,中子数不同,二都均为原子,互为同位素。答案: B
2.美国和墨西哥研究人员将普通纳米银微粒分散到纳米泡沫碳(碳的第五种单质形态)中,得到不同形状的纳米银微粒,该纳米银微粒能有效杀死艾滋病病毒(HIV-1)。纳米泡沫碳与金刚石的关系是学科网(Zxxk.Com)学科网
A.同素异形体 B.同分异构体 C.同系物 D.同位素学科网(Zxxk.Com)学科网
解析:因纳米泡沫碳是碳的第五种单质形态,而金刚石也是碳的一种单质同体,所以二者是由同种元素形成的结构不同的单质,故为同素异形体。答案:A
3.下列各对物质中属于同分异构体的是( )。
A.C与C B.O2与O3
解析:A是同位素,B是同素异形体,C是同一物质,D是同分异构体。答案:D
4.下列各组物质中,互为同系物的是( )。
A. —OH与 —CH3 B. HCOOCH3 与CH3COOC3H7
C. —CH=CH2 与CH3—CH=CH2 D. C6H5OH与C6H5CH2OH
解析:A项二者相差一个氧原子,不是同系物。B项均为酯,结构相似,又分子组成上相差一个CH2原子团,属于同系物。C项不是同一类别的有机物,结构不相似,不是同系物。D项的C6H5OH是苯酚,C6H5CH2OH是苯甲醇,不是同一类别的,结构不相似,不是同系物。答案: B
5.下列各组物质中一定互为同系物的是( )。
A.C3H8、C8H18 B. C2H4、C3H6 C. C2H2、C6H6 D. C8H10、C6H6
解析:A项均为烷烃,分子组成上相差CH2原子团,是同系物。B项不一定互为同系物,当二者都是烯烃时,是同系物;当C3H6是环丙烷时,不是同系物。同理,C项结构不相似,不是同系物。D项可以是不同的类别,不一定是同系物。答案: A
6、人们使用四百万只象鼻虫和它们的215磅粪物,历经30年多时间弄清了棉子象鼻虫的四种信息素的组成,它们的结构可表示如下:
以上四种信息素中互为同分异构体的是( )。
A ①和② B ①和③ C ③和④ D ②和④
解析:这四种有机物均用键线式表示,其中①和③为同种物质;②和④的分子式相同,结构明显不同,互为同分异构体。答案:D
7、萘分子的结构可以表示为 或 ,两者是等同的。苯并[α]芘是强致癌物质(存在于烟囱灰、煤焦油、燃烧的烟雾和内燃机的尾气中)。它的分子由5个苯环并合而成,其结构式可以表示为(Ⅰ)或(Ⅱ)式:
(Ⅰ) (Ⅱ)
这两者也是等同的。现有结构式A B C D
A B C D
其中:与(Ⅰ)、(Ⅱ)式等同的结构式是( );
与(Ⅰ)、(Ⅱ)式同分异构体的是( )。
解析: 以(Ⅰ)式为基准,图形从纸面上取出向右翻转180度后再贴回纸面即得D式,将D式在纸面上反时针旋转45度即得A式。因此,A、D都与(Ⅰ)、(Ⅱ)式等同。也可以(Ⅱ)式为基准,将(Ⅱ)式图形在纸面上反时针旋转180度即得A式,(Ⅱ)式在纸面上反时针旋转135度即得D式。从分子组成来看,(Ⅰ)式是C20H12,B式也是C20H12,而C式是C19H12,所以B是Ⅰ、Ⅱ 的同分异构体,而C式不是。答案:(1)AD (2)B。