|||
强调流形是Hausdorff空间是为了说明流形的无限可分性。
一个很强的说法就是:Hausdorff空间是任意两点的开集都可以不相交的空间。开集不相交,就说明无论两点之间如何靠近,它们之间总不会有公共的相邻点。
再复习流形的定义:实(复)n维流形是这样一个Haustorff空间,它的每点处有开邻域,与实(复)n维线性空间的开集同胚。
再次理解:
开集和开邻域无非是说一个空间的点与周围的点的关系,也就是对空间的微分元素之间的关系。流形的定义,其实就是把实线性空间的定义进行拓展的空间。所进行的拓展,就是剥离对点之间的距离的关注,只保留点之间的顺序的关注,看实线性空间所能变成的样子是什么——这些能变成的空间,就叫流形。——也就是与实线性空间具有同胚的微分结构的空间,就是流形。
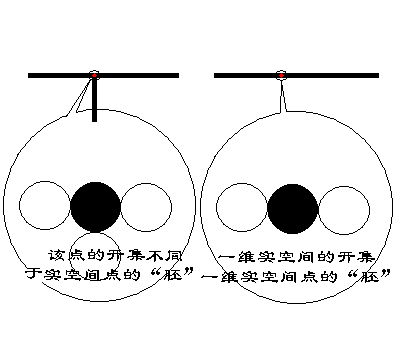
为什么说“圆”是一维的流形呢?

这个“T”就不是流形:
http://blog.sciencenet.cn/blog-33982-524068.html
全部作者的其他最新博文
热门博文导读
0
该博文允许注册用户评论 请点击登录 评论 (2 个评论)
- [2]yushan58
- 所谓登楼撤梯,坐标只是我们达到结论的梯子,达到结论后就不再需要它。这是语言和它所指的东西一个很好案例。
距离是度量空间。
次序(顺序)只是达到了序空间,它如何能够再达到连通,就是邻域空间,也就是拓扑空间了。序空间是一种代数结构,好像离散数学中讨论过。
- [1]yushan58
- 就是剥离对点之间的距离的关注,只保留点之间的顺序的关注,
======================================
因为讲距离总有“数量”概念在其中,而所谓拓扑玩的就是与具体的度量无关,所以顺序(次序)就是在表达这个含义,就是冠军与亚军的次序概念,而它具体的成绩分值(度量)是不重要的。 - 博主回复(2012-1-13 17:35):嗯,是不是讲距离就一定有坐标系,只讲顺序,就不需要坐标系?讲拓扑,就有“脱离坐标系”的功能?
No comments:
Post a Comment