Tuesday, January 29, 2013

二维复数空间中的“点”正是对电子位置的描述,核外电子的轨道不也出现过类似的“捉摸不定”的情况吗？

信息化的本质分享http://blog.sciencenet.cn/u/Babituo

博文

以复数为轴的空间坐标系

已有 989 次阅读2011-4-26 08:36|个人分类:立体逻辑|系统分类:科研笔记|关键词:坐标系 三角形 空间
以1个复数为轴的空间是圆轨空间；（一维的复空间，在欧氏空间中，确实是一个平面）
以2个复数为轴的空间是球壳空间；（二维的复空间）
以3个复数为轴的空间是圈体空间；（三维的复空间，需要动态平移原点，）
球坐标系是一种特殊的二维复空间，特殊在：两个维度的复数模保持相等。类似直角平面坐标中的45度直线。
圈体空间是特殊的三维复空间，特殊在：三个复数的模必须闭合为一个三角形。
一般的三维复空间是怎样的呢？已经无法想象了，在欧氏空间中已经是超出三维了。
圈体或者不是三维复空间，而只是二维复空间中的一条曲线？
对了：圈体是二维复空间中的一条曲线。当圈体做全周的体旋，扫过的空间，就是球壳空间。
那么，球体是二维复空间中的一条直线，而且是斜率为1的直线。
球壳空间是二维复空间中满足如下条件的一条曲线（面）：复数x的模大于r1; 复数y的模小于r2;(r2>r1).
“一个数，按其大小顺序经历其所有可能的值，形成其一维的数值空间，也就是其一维的数轴”的定义来理解“复数的1维数轴”就比较容易了。
不知道这样的“降维”能带来什么好处，应该会有不少好处。
当初看到彭罗斯等人那么强调复数的奥妙，现在才真正开始有点领悟了。
两个复数的“正交”，是三旋中的面旋和体旋的正交。问题是：如果两个复数的模（长度）不等，我们就不能像“在直角坐标系中给出的X,Y就能交汇到空间中的一点”那样，让两个复数也交汇到“一点”。
怎么办？
是舍弃让复数可以正交的想法？还是寻找新的“点”的含义？
全世界的人直接选择舍弃，我试图去寻找一下，当然，我是相信一定能找到才要去找的，而且，我相信，新的点的含义是能和原来的点的含义兼容的。显然地，只要加上一个约束，让两个复数的模必须相等，我们要找的点，不过就是球面上的点而已。如果我们放开这个约束，是不是“点”的“灵魂出壳”了呢？极有可能。
这么说，体旋是灵魂（思想）运动，面旋是身体运动的猜想，就可能有答案了。
当然，不要将灵魂神秘化，玄乎化来理解，灵魂和身体，只是磁和电的化身而已。
约束，代表什么？代表有函数关系，函数关系代表什么，代表是空间中的一条曲线，不是吗？
所以，球空间，只是二维复数空间中的“一条曲线”而已。曲线之外还有大量的信息，球形空间是不能严格代表二维复数空间的。类似：圈空间也不能。
猛然又让我醒悟：我们对核外电子的轨道不也出现过类似的“捉摸不定”的情况吗？
电子云，不正是一个“球壳”吗？，难道...?
天哪，二维复数空间中的“点”正是对电子位置的描述！
原来，我们不是不知道电子的精确位置，我们只是用错了“点”啊！
终于想明白了：
二维的复数空间，就是一个确定性和不确定性统一的球形空间，也就是是“势与实”，“电与磁”统一，并可“错位”分布的球形空间。
这个空间中的“点”，不是一个确定的欧氏空间中的点，而是一条球壳间的“辐线段”——“一条纤维”。
这条辐线段的长度，正是线旋的半径！
也就是说，当线旋半径等于0时，二维复数空间成为一个标准的球面体。
而当线旋半径大于0时，二维复数空间成为一个标准的圈面体。
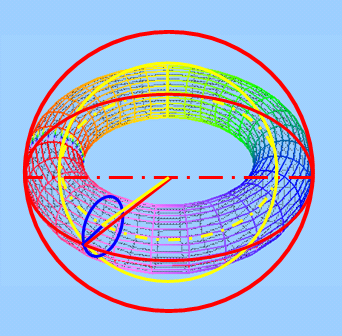
它的身体在这，灵魂却可能在那；
它的电在这，磁却可能在那；
但却总是形影不离。
灵魂——只不过是真实存在的量子群的磁效应而已；
身体——只不过是真实存在的量子群的电效应而已。
以复数为轴的空间坐标系，可以解密这一切。


http://blog.sciencenet.cn/blog-33982-437355.html
分享到：
收藏分享举报

全部作者的其他最新博文

热门博文导读

相关博文

3洪昆辉陈辉vigorous

发表评论 评论 (6 个评论)

[6]邱嘉文 2011-5-6 16:38
本文纯属“开小差”。复数坐标系下的三旋描述，已经是应用层的问题了。和理论思想的核心内容关系不大。
[5]邹晓辉 2011-5-4 17:42
对象（物？）、选择（意！）、符号（文？）

一个耐人寻味的问题：点，究竟属于那个维度？

http://bbs.sciencenet.cn/home.php?mod=space&uid=94143&do=blog&quickforward=1&id=440404
[4]邹晓辉 2011-5-4 17:03
嘉文，你这里是否犯了术语称谓不一或逻辑思维矛盾的错误？因为，点，既可在一维的线（如：数轴）上，也在二维的面（如：复平面）上，还在三维的立体（如：笛卡尔坐标系描述的空间向量或立体几何体）上。晓辉
博主回复(2011-5-4 17:35)：关键的问题是：读者是否能通过我的表达，知道我用“点”这个词语，分别指称的对象是什么？这些对象，看上去很有差异，为什么还可以称为“点”？有没有更好的名称来区分它们？这才是正确的讨论思路。
[3]陈辉 2011-4-27 09:30
球形几何学的内容属于非欧几何学
博主回复(2011-4-27 09:34)：我已经在文章中补充了关于“球形空间”对“二维复数空间”所产生的“信息失真”的问题了，请关注。
博主回复(2011-4-27 09:32)：是的，是欧式几何空间概念支撑下的非欧几何。
[2]陈辉 2011-4-27 07:16
一维复空间是【点】的轨迹，构成复空间中的一条线
二维复空间是【线】的轨迹，构成复空间中的一个面
三维复空间是【面】的轨迹，构成复空间中的一个体

复空间是个【球形空间】
博主回复(2011-4-27 08:36)：球形，是没错的。
“球形”的意思是：因为我们习惯了在欧式空间中思维；“球形”只是我们为了理解新构造的空间，不得不到我们能理解的欧氏空间中来寻找的替代形，但既然是替代，是要付出某些信息失真的。
如果我们能直接建立新空间的理解构造，我们不再需要转换到欧氏空间中，就能获得我们自以为是的“理解”的话，我们就能见识到真正的，没有失真的新空间。
[1]邱嘉文 2011-4-26 09:26
请按“一个数，按其大小顺序经历其所有可能的值，形成其一维的数值空间，也就是其一维的数轴”的定义来理解“复数的1维数轴”。
at

No comments:

Post a Comment