延迟微分方程
一个延迟微分方程是一种微分方程,其在当前时间的时间导数取决于它在以往时间的解,还可能取决于它在以往时间的导数:
一个初始历史函数

需要被指定,而不是一个简单的初始条件. 量

和
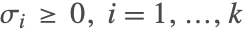
被称为延迟或者时间滞后(time lags). 延迟可能是常量,
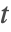
的函数
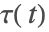
和
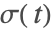
(时间依赖延迟)或者函数

和
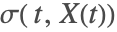
(状态依赖延迟). 具有导数的延迟

的延迟方程被称为中立型延迟微分方程(NDDE).
在
NDSolve 中的方程处理代码的设计使用户可以基本上按数学符号输入一个延迟微分方程.
x[t-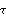 ] ] | 具有延迟  的应变量 的应变量 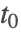 |
x[t /; t≤t0]= | 对于  小于 小于  的情况 ,把初始历史函数指定为表达式 的情况 ,把初始历史函数指定为表达式 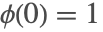 |
目前,在
NDSolve 中延迟微分方程的实现只支持常量延迟.
| Out[1]= | 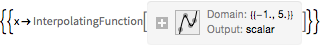 |
| Out[2]= | 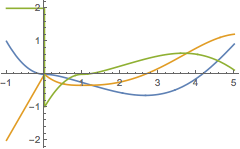 |
为了简单起见,本文假设积分总是从较小到较大的

进行. 但是,如果给出的初始历史函数针对大于

的值,并且延迟是负数,
NDSolve 也支持其他方向的积分,.
在负
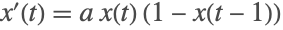
方向上,求解一个二阶延迟微分方程.
| Out[3]= | 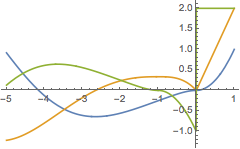 |
与常微分方程的比较和差异
虽然延迟微分方程看起来很像常微分方程,它们的理论更加复杂,并且与常微分方程有一些令人吃惊的不同之处. 本节将给出这些差异的一些例子.
查看对于不同的初始历史函数

的解.
只要初始函数满足

,
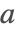
的解总是1.
[Z06] 使用常微分方程,用户总数可以从一个解对时间向后积分,以获得初始条件.
对于参数

的不同值,考查

的解.
对于

,解是单调的,对于

解是振荡的,而对于
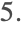
解接近一个极限环. 当然,对于标量微分方程,解是单调的,不依赖于

.
对于两个接近的常量初始函数,求解 Ikeda 延迟微分方程,
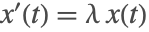
.
| Out[90]= | 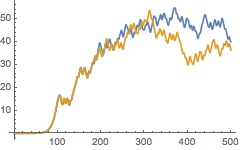 |
这个简单的标量延迟微分方程具有混沌解,而上面显示的运动很像布朗运动. [
S07] 当延迟

的增加超过
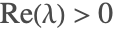
时,一个极限环出现了,之后,将跟随一个周期倍增级联,并在

之前走向混沌.
| Out[104]= |  |
稳定性对于延迟方法也复杂得多. 众所周知,线性常微分方程测试方程

当

时具有渐进稳定解,而如果

则是不稳定的.
最接近的相应的延迟微分方程是

. 即使你只考虑实数的

和

,情况就不会这么清晰. 下面一些解的图形显示了这一点.
该解对于

和
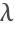
是稳定的.
| Out[110]= | 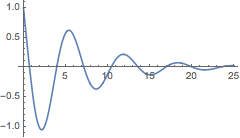 |
该解对于
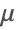
和
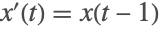
是不稳定的.
| Out[111]= | 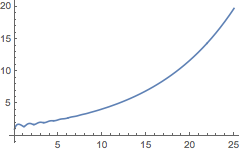 |
所以,取决于

的值,在

的时候该解可以是稳定的,而

则是不稳定的. 下面建立一个
Manipulate 使得用户可以查看

平面.
通过变化
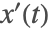
和

考查解.
不连续性的传播和平滑化
不连续性由延迟而传播的方式是延迟微分方程的一个重要特征,并且对于求解它们的数值方法具有深刻的影响.
| Out[3]= |  |
| Out[4]= | 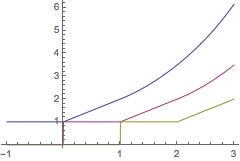 |
在上面的例子中,

是连续的,但是在
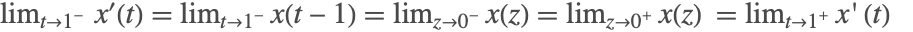
处,
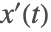
有一个跳跃不连续性,因为从左边趋近,值为

,由初始历史函数的导数
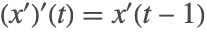
给定,而当从右边趋近时,值由延迟微分方程给出,有
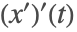
.
接近

时,根据

在

处的连续性,我们有

,所以

在
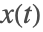
处是连续的.
对方程求导,我们可以得到如下结论:
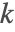
所以
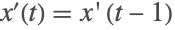
在

处有一个跳跃不连续性. 使用和上面基本相同的讨论,我们可以得到如下结论:在

处,二阶导数是连续的.
| Out[12]= |  |
| Out[11]= | 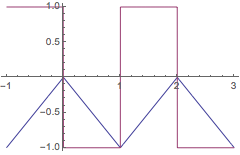 |
很容易看出解是分段的,但

是连续的. 不过,
一般说来,对中立型延迟微分方程不存在不连续性的平滑化.
不连续性的传播从数值求解的立场上看非常重要. 如果忽略了可能的不连续点,那么求解器的阶数将会降低. 如果已知不连续点,可以通过积分只积到不连续点,然后使用新的函数值在刚过该点的时候重新开始该方法来找到更加准确的解. 这样,积分方法用于解的平滑部分,可以产生更好的准确性和更少的被拒步长. 从任何给定的不连续点,将来的不连续性点可以从延迟确定,并且可以通过把它们作为要定位的事件来检测到.
当存在多个延迟时,不连续性的传播可以变得相当复杂.
| Out[109]= |  |
| Out[110]= | 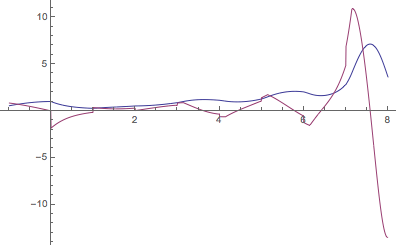 |
很明显,从图形中看出,在每个非负整数上有一个不连续点,正如对中立型延迟
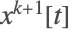
所预期的那样. 但是,查看二阶和三阶导数,可以明显看出也存在与诸如

、

、

的点相关的不连续点,它们从位于

的跳跃不连续性处传播而来.
| Out[111]= | 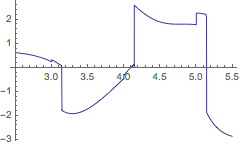 |
事实上,有一整个不连续点的树状结构可以在时间向前方向上传播. 一种对一个解区间确定和显示不连续点树的方式在下面的小节中给出.
不连续点树
定义一个命令,它给出具有给定延迟的延迟微分方程的不连续点传播的图示.
获得上述例子直到

的不连续点树.
| Out[113]= | 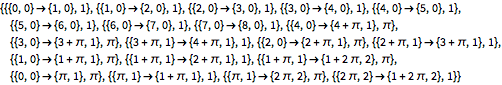 |
定义一个命令,它显示对于阶数为

的不连续点,

和
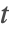
的图形.
画出分层图,把不连续图作为每个不连续点的工具提示条显示.
| Out[117]= |  |
存储历史数据
一旦解已经进行到第一个不连续点之后,一些需要计算的延迟值就会在初始历史函数的范围以外,需要使用计算得到的解来获取这些值,这通常是通过在前面采取的步骤中插值实现. 为了使延迟微分方程的解准确,关键是插值要与该方法一样准确. 这是通过使用常微分方程积分方法的稠密输出 (即用户在
NDSolve 中使用选项
InterpolationOrder->All 时得到的输出)来实现的.
NDSolve 对从绝大部分方法中获取稠密输出具有一个通用的算法,所以用户可以使用任何方法作为积分器. 一些方法,包括对于延迟微分方程的默认方法,具有它们自己的获取稠密输出的方式,这通常比通用方法更加有效. 阶数足够低的方法,如具有

的

就可以使用一个三次 厄米(Hermite) 多项式作为稠密输出,所以基本上在保持历史上没有额外代价.
由于历史数据频繁地被访问,所以需要有一个快速查找的机制,以确定在哪个步骤插值. 在
NDSolve 中,这使用一个二分查找机制实现,与实际函数计算的代价相比,搜索时间可以被忽略.
每个成功的步骤的数据会在尝试下一个步骤之前保存,并且保存在一个可以有效重地复展开的数据结构中. 当
NDSolve 产生解时,它简单地采用这个数据,并且把它重组为一个
InterpolatingFunction 对象,所以延迟微分方程的解总是使用稠密输出返回.
步进的方法
对于常量延迟,有可能获得作为固定时间点的所有不连续点. 步进方法的思想是简单地在这些区间内对平滑函数进行积分,并且在下个区间重启,确保从右边重新计算函数. 只要间隔没有变得太小,该方法在实践中相当不错.
目前用于
NDSolve 实现的方法就是基于步进的方法.
步进的符号方法
本节定义了一个步进的符号方法来说明该方法的工作方式. 请注意,为了保持代码更简单并且更接近要点,它不会做任何实变量检查. 此外,数据结构和历史查找也没有用有效的方式实现,但是对于符号解,这是一个小问题.
求延迟微分方程
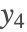
的解,其中
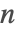
.
| Out[24]= | 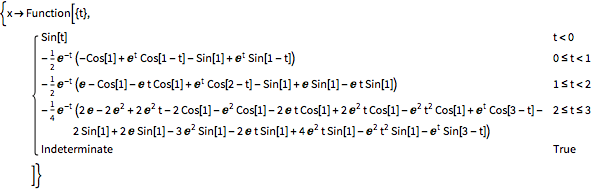 |
| Out[25]= | 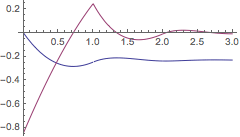 |
| Out[27]= |  |
求中立型延迟微分方程

的解,其中
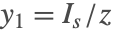
| Out[28]= | 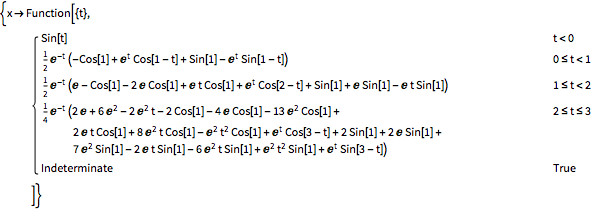 |
| Out[29]= | 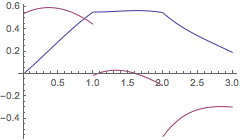 |
| Out[31]= | 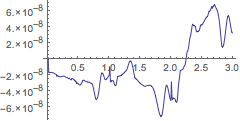 |
对符号参数值,符号方法仍然适用,只要
DSolve 仍然可以找到解.
寻找具有符号系数的一个简单的线性延迟微分方程的解.
| Out[32]= |  |
代码设计为可以采用列表的原因是使得它适用于方程组.
| Out[33]= |  |
| Out[34]= | 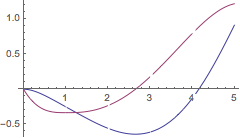 |
| Out[36]= | 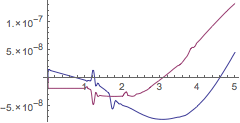 |
由于该方法计算不连续点树,它对于多个常量延迟也将适用. 但是,在多个延迟的情况下,解可能很快变得相当复杂,而
DSolve 可能因使用庞大的表达式而停滞.
| Out[37]= |  |
| Out[38]= |  |
| Out[40]= | 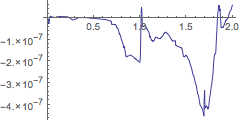 |
示例
具有延迟的 Lotka-Volterra 方程
Lotka-Volterra 系统对于动物物种的生长和相互作用建模,假设一个物种对于另一个物种的影响是连续的并且是即刻的. 一个物种对另一个物种的延迟效应可以通过在相互作用项中引入时间滞后来建模.
在没有延迟的情况下,
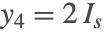
,系统 (1) 具有一个不变量
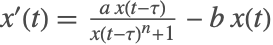
,它对于所有
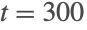
是常量,而且具有一个(中立型)稳定的周期性解.
| Out[16]= | 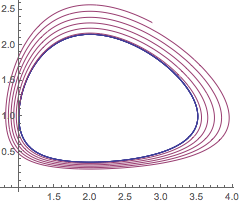 |
在这个例子中,即使是一个很小的延迟,其效果也使周期性轨道变得不稳定. 已经证明,在延迟 Lotka-Volterra 系统中采用不同的参数,存在全局吸引性平衡点.[
TZ08]
酶动力学
其中
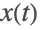
是一个保持在固定水平的基板供应,而最终产品
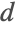
的

个分子抑制反应步骤

. [
HNW93]
通过引入一个离开平衡点的小扰动来考查 (1) 的解.
Mackey-Glass 方程
Mackey-Glass 方程

在对白血细胞的产生进行模拟时提出的. 具有周期性的(periodic)和混沌(chaotic)解.
下面是Mackey-Glass方程的周期性的解. 该图形只显示
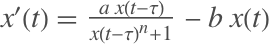
之后的情况,以使得瞬时态消失.
| Out[32]= |  |
| Out[45]= | 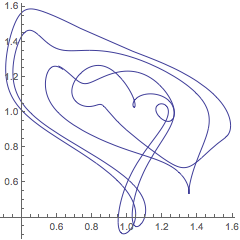 |
下面显示的是在三维中解
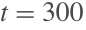
的嵌入.
| Out[15]= | 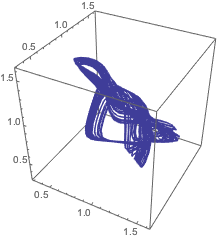 |
使用另一种方法计算混沌解,并且对使用不同方法计算得到的
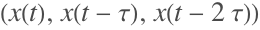
之间的差异

画出
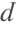
的图形.
| Out[17]= |  |
在时间间隔的末尾,方法之间的差异的数量级是1. 大偏差对于混沌系统很典型,在实际中,它不可能甚至也没有必要对一个大的区间获得一个相当准确的解. 但是,如果用户真想要一个高质量的解,
NDSolve 则允许用户使用较高的精度. 对于更高精度的延迟微分方程,推荐使用

方法.
| Out[19]= |  |
 需要被指定,而不是一个简单的初始条件. 量
需要被指定,而不是一个简单的初始条件. 量  和
和 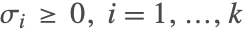 被称为延迟或者时间滞后(time lags). 延迟可能是常量,
被称为延迟或者时间滞后(time lags). 延迟可能是常量,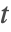 的函数
的函数 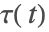 和
和 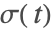 (时间依赖延迟)或者函数
(时间依赖延迟)或者函数  和
和 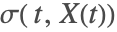 (状态依赖延迟). 具有导数的延迟
(状态依赖延迟). 具有导数的延迟  的延迟方程被称为中立型延迟微分方程(NDDE).
的延迟方程被称为中立型延迟微分方程(NDDE).
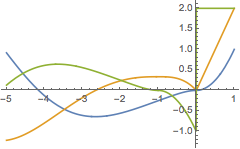










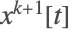 所预期的那样. 但是,查看二阶和三阶导数,可以明显看出也存在与诸如
所预期的那样. 但是,查看二阶和三阶导数,可以明显看出也存在与诸如  、
、 、
、 的点相关的不连续点,它们从位于
的点相关的不连续点,它们从位于  的跳跃不连续性处传播而来.
的跳跃不连续性处传播而来.
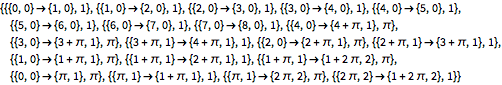

 的
的  就可以使用一个三次 厄米(Hermite) 多项式作为稠密输出,所以基本上在保持历史上没有额外代价.
就可以使用一个三次 厄米(Hermite) 多项式作为稠密输出,所以基本上在保持历史上没有额外代价.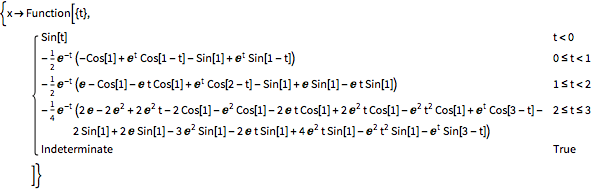


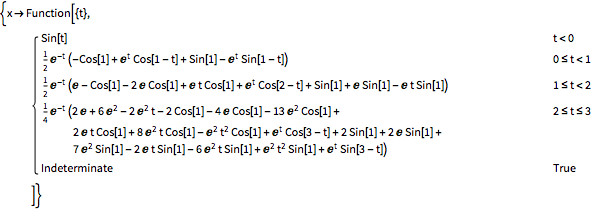














 方法.
方法.


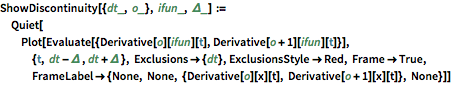


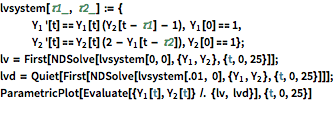

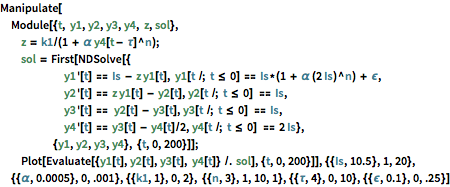
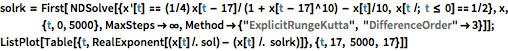

No comments:
Post a Comment