Thursday, May 22, 2014

冯·诺伊曼 abel 测度问题便从Rn推广到了一般的非阿贝尔群．而巴拿赫关于R2的一切子集使用同一测度的可能性被证明对阿贝尔群的所有子集也成立

关于冯·诺伊曼是严格意义的数学家和计算机学家的证明(2)



所有跟贴·加跟贴·新语丝读书论坛http://www.xys.org/cgi-bin/mainpage.pl
送交者: BerkeleyWolf 于 2006-6-07, 18:52:01:回答: 关于冯·诺伊曼是严格意义的数学家和计算机学家的证明(1) 由 BerkeleyWolf 于 2006-6-07, 18:44:47:声明: 所有的内容都是从网上转载编辑的.冯·诺伊曼同学在纯粹数学上的贡献　　冯·诺伊曼在纯粹数学方面的工作集中于1925—1940年，主要可分为以下六个方向。
　　1．集合论与数学基础
　　本世纪初，为了克服悖论给G．康托尔(Cantor)集合论带来的困难，并系统整理康托尔的理论与方法，人们开始致力于公理化方法的研究．1908年，出现了两个著名的公理系统：E．策梅罗(Zermelo)的系统[后由A．弗伦克尔(Fraenkel)和A．斯科朗(Skolem)修改补充，成为ZF公理系统]和B．罗素(Russell)的类型论．
　　冯·诺伊曼很早就对集合论问题感兴趣．1923年还在苏黎世就读期间，他发表了自己的第二篇论文“超穷序数引论”(Zur Einfhrung der transfiniten Ordnungszahlen)，力图将康托尔的序数概念“具体化、精确化”．在康托尔的定义中，序数是良序集的序型，而根据ZF公理系统，序型的存在性是无法证明的．冯·诺伊曼借助于ZF公理系统中初始截断的概念和无穷公理，给出了序数及超限序数形式化的新定义，这种定义一直沿用至今．
　　此后六七年中，他积极传播公理化的思想，并试图建立更具形式化和精确性的公理系统．1923年，他向德国《数学杂志》(Ma－thematische Zeitschrift)编辑部提交了长篇论文“集合论的公理化”(Die Axiomatisierung der Mengenlehre)，施密特代表编辑部把论文推荐给集合论方面的权威弗伦克尔．经过与弗伦克尔详尽地探讨，冯·诺伊曼根据原文写出一篇介绍性文章“集合论的一种公理化”(Eine Axiomatisierung der Mengenlehre)，于1925年发表．
　　“集合论的公理化”后来成为冯·诺伊曼的博士毕业论文．它所建立的公理体系经P．贝尔纳斯(Bernays)和K．哥德尔(Gdel)完善之后，形成了公理化集合论中又一新的系统——NBG系统．
　　NBG系统不像ZF系统那样，把集合与从属关系作为原始概念，并采取限制集合产生的办法来达到排除悖论的目的，也不同于类型论中以集合与层次的语言描述集合体系．它的特点是在“集合”与“属于”之外，引入了“类”作为不定义概念，比集合的概念更具概括性．类分为集合和真类，规定真类不能作为类的元素．这样，就排除了由“所有集合的集合”产生悖论的可能性．
　　与ZF公理系统相比，NBG系统保留了更多、更有用的论证方法．而且在ZF系统中，包含着由无穷多条公理组成的公理模式，NBG系统则不含公理模式，是一有穷公理系统，有着如同初等几何公理那样简单的逻辑结构，这是它最主要的优点．
　　现已证明，NBG系统是ZF系统的扩充．哥德尔在证明选择公理与连续统假设同其他公理的相容性时，就受到了NBG系统的启发．到今天，NBG系统仍是集合论最好的基础之一．
　　与集合论公理化的工作相适应，冯·诺伊曼在20年代后期参与了希尔伯特的元数学计划．1927年的文章“关于希尔伯特的证明论“(Zur Hilbertschen Beweistheorie)对数学形式主义的基本概念进行了阐释．它指出，希尔伯特元数学计划所提出的各种问题，虽经希尔伯特本人及贝尔纳斯、W．阿克曼(Ackermann)等人的努力而有所进展，但从总体上而言仍未得到令人满意的解决．尤其是阿克曼关于自然数论无矛盾性的证明，不能在古典分析中实现．
　　1931年，哥德尔不完全性定理提出之后，希尔伯特计划的完全实现落空了．对此，冯·诺伊曼并未感到过分惊奇，因为早在1925年发表的“集合论的一种公理化”中，他便隐约地预见到哥德尔的结论：任一形式化体系中都存在着本系统内无法判定的命题．原文的最后一句话是：“暂时，除了陈述集合论本身的缺陷外，我们还能做什么呢？没有一种已知的方法可以避免其中的困难．”他认为，“由哥德尔的结果应当引出一条新的途径，去理解数学形式主义的作用，而不应把它当作问题的结束．”他本人对数学基础保持着长久的兴趣，并在后期关于计算机逻辑设计和机械化证明中得到体现．
　　2．测度论
　　测度论在冯·诺伊曼的整个研究工作中并非处于中心地位，但他给出了许多很有价值的方法和结果．
　　在1929年的“一般测度理论”(Zur allgemeinen Theorie desMasses)一文中，冯·诺伊曼对群的子集讨论了有限可加测度．n维欧氏空间Rn中的“测度问题”是：Rn的幂集上，是否存在一非负、正规化且关于刚体运动不变的可加集函数？F．豪斯多夫(Hau－sdorff)和S．巴拿赫(Banach)证明：测度问题在n为1和2时有无穷多个解，在其他情况下无解．这个结论给人的感觉是：当维数由2变为3时，空间的特性发生了根本的、难以捉摸的变化．冯·诺伊曼则指出，问题在本质上是属于群论的，造成性质差异的根源在于群的变化而非空间的变化．探讨测度问题的可解性，需要用到群的可解性这一代数概念．
　　他继续运用群论的思想，分析了豪斯多夫-巴拿赫-塔尔斯基(Tarski)悖论：Rn(n≥3)中两个不同半径的球，可以分别被分解为有限个互不相交的不可测子集，使两球的子集间可建立起两两全等的关系(在n为1或2时，这种分解不存在)．他解释说，这是因为在n为3或更大时，正交群包含着自由非阿贝尔(Abel)群，而在小于3时则不然．
　　这样，测度问题便从Rn推广到了一般的非阿贝尔群．而巴拿赫关于R2的一切子集使用同一测度的可能性被证明对阿贝尔群的所有子集也成立．最后，他得出结论：所有可解群都是可测度的(即某种测度能够引入到可解群上)．
　　这篇文章属于最早将集合论的结果从欧氏空间推广到更一般的代数和拓扑结构中去的工作之一．从那时起，这种思想方法开始受到了更广泛的重视．
　　同一时期，匈牙利数学家A．哈尔(Haar)提出这样一个问题：在Rn中是否有一种挑选可测子集的方法，使得每个子集均与给定的集合等价，并且选择过程保持有限集运算？冯·诺伊曼给出了肯定的回答，并把结论推广到可测函数的情形．这成为解决测度分解问题的出发点．1935年，他还与M．斯通(Stone)合作，讨论了更一般的问题：A是一布尔代数，M为A的理想，何时存在A的子代数，使A到A／M的映射限制在子代数上时为同构？他们给出了存在性的各种充分条件．
　　另一成果是他在1934年对紧致群证明了哈尔测度的唯一性(在相差常数因子的意义下)．证明过程中构造了紧致群上连续函数的“不变平均”(invariant means)，用到不同于哈尔的方法来引进测度.这些方法在后来他与S．博赫纳(Bochner)研究可分拓扑群上殆周期函数时得到了系统的应用．
　　1933—1934年，冯·诺伊曼在高级研究院作过有关测度论的报告，非常详细地阐释了欧氏空间中勒贝格测度的古典理论，并推广到抽象测度空间中．报告的内容在很长一段时间内是美国在测度论方面的主要资料来源，1950年由普林斯顿出版社编辑成为《函数算子》 (Functional operators)一书．　　3．遍历理论
　　冯·诺伊曼在这一领域的首要成就，是证明了平均遍历定理(mean ergodic theorem，亦称弱遍历定理)．19世纪70年代，L．玻尔兹曼(Boltzmann)提出了统计力学中的遍历性假设，并希望以此为前提，推导出保测变换的空间平均等于(离散)时间平均，这就是玻尔兹曼计划．
　　从数学上实现这一计划，首先需要证明作为时间平均的极限的存在性．1931年，B．库普曼(Koopman)和A．韦伊(Weil)同时发现，由保测变换诱导出的函数算子是酉算子．它给冯·诺伊曼以很大启示．当时，他正致力于算子理论的研究，这一发现促使他尝试着用希尔伯特空间的自共轭算子去解决存在性问题．很快，他便提出并证明了遍历理论的第一个重要定理——平均遍历定理.在这一结果发表(1932年)之前，冯·诺伊曼把它介绍给了G．D．伯克霍夫(Birkhoff)和库普曼．伯克霍夫将“依平均测度”意义下的收敛改善为“处处收敛”，得出了更强的结论——逐点遍历定理(pointwise ergodic theorem，亦称个体遍历定理)，并于1931年12月率先发表．
　　尽管如此，由于伯克霍夫与库普曼在1932年撰写了“遍历理论的近期发展”(Recent contributions to the ergodic theory)，使学术界了解到遍历定理产生的前因后果，冯·诺伊曼的首创性工作得到了肯定．
　　不久，第33卷《数学纪事》(Annals of mathematics，1932)又刊登了他颇具影响力的文章“古典力学中的算子方法”(ZurOperatorenmethode in der klassischen Mechanik)，这标志着对遍历理论系统研究的开端．
　　论文首先给出了平均遍历定理的详尽证明，然后推出6条重要的定理．第一条是分解定理(decomposition theorem)：任何保测变换均可分解为若干遍历变换的直积分．它说明在所有保测变换中，具有遍历性的是最基本、最重要的，任何保测变换都可由它们构造而得．
　　定理2则进一步指出，单参数保测变换群的分类问题在本质上可归结为对遍历变换进行分类．
　　保测变换的分类问题后来成为遍历理论的中心问题，其中最关键的第一步，当属冯·诺伊曼与P．哈尔莫斯(Halmos)1942年共同证明的结论：
　　f1和f2分别是有限测度空间X1和X2上的保测变换，U1和U2分别是X1，X2在L2上诱导出的酉算子．若f1，f2有离散谱，则f1与f2同构当且仅当U1和U2作为希尔伯特空间上酉算子时是相同的．
　　冯·诺伊曼在处理遍历理论的问题时，往往着重于测度和谱的内在联系．定理5就是关于离散谱的典型结果：对于具有纯点谱的酉算子U(由遍历变换诱导而得)，其谱实际上构成实数群的一可数子群；反过来，实数群的每个无穷可数子群均可作为某些遍历变换所诱导的酉算子的纯点谱．
　　与此对应，又有冯·诺伊曼和库普曼关于连续谱的混合定理(mixing theorem)．它断言：遍历变换的几何性质(混合性)与酉算子的谱性质(无非平凡的特征值)是等价的．
　　对于冯·诺伊曼在测度论和遍历理论方面所取得的成果，哈尔莫斯给予了如此的评价：“从文献数量上看，它们尚不及冯·诺伊曼全部科学论著的十分之一，但就质量而言，即使他从未在其他方面作过研究，这些成果也足以使他在数学界享有永久的声望．”　　4．群论
　　冯·诺伊曼的一个著名成果，是在1933年对紧致集解决了希尔伯特第五问题．早在1929年，他曾证明对连续群有可能改变参数，使群的运算成为解析的．具体地说，对于n维空间中的线性变换群，它有一正规子群，可以被解析地且按有限个参数一一对应的方式局部表出．这是第一篇对解决希尔伯特第五问题做出贡献的文章．
　　1933年，他在《数学纪事》第34卷上发表“拓扑群中解析参数导论”(Die Einfhrung analytischer Parameter in topologischen Gruppen)，证明每个局部同胚于欧氏空间的紧致群允许一李群结构．这样，希尔伯特第五问题在紧致群的条件下得到了肯定的回答．
　　问题的解决用到了彼得(Peter)-外尔积分在群上的类比、施密特的函数逼近定理及L．E．J．布劳威尔(Brouwer)关于欧氏空间的区域不变性定理，体现出冯·诺伊曼丰富的集合论与实变函数知识以及他对积分方程、矩阵计算技巧的熟练应用．
　　另一项工作亦同群论相关：群上的殆周期函数(almost pe－riodic function)理论．他把H．玻尔(Bohr)首创的实数集上殆周期函数概念扩展到任意群G中，继而在新的殆周期函数理论与彼得、外尔的群表示理论之间建立起联系.他由此指出，群上的殆周期函数构成了群表示理论的最大适用范围．　　5．算子理论
　　对算子理论的探索贯穿了冯·诺伊曼的整个科学生涯，这方面的论文占他全部著述的三分之一，他在这个领域有着20多年的领导地位．
　　1927—1930年，他首先给出了希尔伯特空间的抽象定义，即现在所使用的定义．然后，对于希尔伯特空间上自共轭算子谱理论从有界到无界的推广，做了系统的奠基性工作：引入稠定闭算子的概念，给出无界自共轭算子、酉算子以及正规算子的谱分解定理，指出了对称算子和自共轭算子在性质上的差异，还与外尔共同研究了无界算子经过扰动后谱的变化规律．
　　冯·诺伊曼的谱理论的形成，加上1933年巴拿赫所著《线性算子理论》(Thorie des operations linaires)一书的问世，标志着数学领域中又一新的分支——泛函分析的诞生．
　　20年代，E．诺特(Noether)和E．阿廷(Artin)发展了非交换代数理论，冯·诺伊曼意识到这是对矩阵论极好的阐释和简化，他尝试着将有关概念扩展到希尔伯特空间上的算子代数中，由此产生了“算子环”的概念：关于弱(或强)算子拓扑为闭且含有恒等算子I的＊子代数称为算子环．算子环可以认为是有限维空间内矩阵代数的自然推广，后来被人们称为冯·诺伊曼代数，以示对冯·诺伊曼的纪念．而在同构意义下，它又可称作W*代数．
　　算子环的正式定义出现在冯·诺伊曼1929年的论文“函数运算代数和正规算子理论”(Zur Algebra der Funktionaloperati－oren und Theorie der normalen Operatoren)中．这篇论文还包括了“交换子”(commutant)、“因子”(factor)等重要定义，以及二次交换子定理(double commutant theorem).
　　从1935年开始，冯·诺伊曼在F．J．默里(Murray)的协助下，又写出了题为“论算子环”(On rings of operators)的系列文章．
　　他们的首要结论是：算子环可以表示为因子的连续直积分．因此，对算子环的研究便归结为对因子的研究．
　　受经典非交换代数理论的启示，人们曾推测所有因子均同构于(H)．冯·诺伊曼和默里在“论算子环I”中证明：当因子包含极小射影时，它同构于(H)．但同时，他们又应用遍历论的技巧，构造出一类重要的例子，说明并非所有的因子都有极小射影，因而有关因子的性质远非人们推测的那样简单．
　　他们在因子的射影之间建立了序关系，使之具有可比性．而这种序关系又可用维数函数(定义于因子的等价类之上)来表述.通过群测度空间的构造，他们得到了Ⅱ1型和Ⅱ∞型因子．1940年的“论算子环Ⅲ”又给出了Ⅲ型因子的例子．
　　继因子的分类和各类因子存在性的证明之后，一个重要的问题是：这种分类是否完成了因子的代数分类？即某给定类型中的全体因子是否同构？冯·诺伊曼和默里花去大量时间考察这个问题，最终构造出两个新的Ⅱ1型因子并证明它们是非同构的，从而给了原问题否定的回答．　　6．格论
　　冯·诺伊曼在研究希尔伯特空间算子环时，遇到了一类完备有补模定义L为连续几何(continuous geome－try)，并构造出一类重要的连续几何：对任意可除环F和自然数n，F上的2n维子空间构成2n—1维射影几何PG(F，2n—1)．将它度量完备化之后得到的有补模格就是连续几何，记为CG(F)．他证明了希尔伯特空间中的Ⅱ1型因子具有与CG(F)同构的不变子空间格．
　　正则环(regular ring)是冯·诺伊曼引入的另一新概念：A是有单何的表示有着密切联系：连续几何L与某正则环A的主左理想构成的格同构．也就是说，将A分解为诸理想的直和，对应于把L分解为诸格的直积的问题．
　　在这些结论的证明过程中，冯·诺伊曼又发展了一些新的思想方法，其中主要是关于格的分配性：数对的分配性、独立元的分配性和无穷分配性等．他最早发现，在布尔代数中，交与并的运算必然是无穷分配的，而这种分配性又等价于连续性．
　　他在格论方面的工作大部分未能及时发表，主要通过1935—1937年高级研究院的讲义《复域几何》(Geometry of complexdomains)、《连续几何》及美国科学院会议录得以保存和传播．


http://episte.math.ntu.edu.tw/articles/mm/mm_13_3_01/page2.html
 Shannon 熵給出了這個樣本空閒的不確定度──$n\log{2}$。






 
上頁　1│2│3│4　次頁
熵 (Entropy) （第 2 頁） 李天岩
 
．原載於數學傳播十三卷三期
．作者當時任教於美國密西根州立大學數學系
‧對外搜尋關鍵字


 
2. Kolmogorov 熵
我們再來做旋轉光滑硬幣的遊戲。為了方便起見， 我們稱硬幣的正面為 l，反面為 0。讓我們考察連續旋轉 n 次， 其每次正反面出現的各種可能性。旋轉一次，有兩個可能性， 或正面朝上，或反面朝上，即 1,0；旋轉兩次有 4=22 種可能性， 即 11,10,01,00;一般來說，旋轉 n 次則有 2n 種可能性。 把連續旋轉 n 次的任一可能結果看成一個「基本事件」， 我們則得到一個具有 2n 個基本事件的樣本空間， 其每一基本事件有同樣的概率 2-n。 上節中所談 Shannon 熵給出了這個樣本空閒的不確定度──$n\log{2}$。 現在我們要進一步問的是：如果我們已知旋轉硬幣第一次，第二次，… 第 n-1 次的結果，那麼第 n 次會是正面或會是反面的不確定度該是多少？ 我們希望能用數學上的語言來描述這個問題。 首先讓我們來考慮定義在 [0,1] 上的函數 $f(x)=2x(\mbox{mod} 1)$，也就是

\begin{displaymath} f(x)=\left\{ \begin{array}{ll} 2x & 0 \leq x < \frac{1}{2} \\ 2x-1 & \frac{1}{2} \leq x \leq 1 \end{array}\right. \end{displaymath}


（見圖2-1），取 Lebesgue 測度 m 做為 [0,1] 上的測度， 令 $\overline{A}=\{ [0,\frac{1}{2}],[\frac{1}{2},0] \}$ 為 [0,1] 上的一個劃分 (partition)， 則 $f^{-1}(\overline{A})= \{ f^{-1}([0,\frac{1}{2}]),f^{-1}([\frac{1}{2},1])\}$ $=\{ [0,\frac{1}{4}] \cup [\frac{1}{2},\frac{3}{4}],$ $[\frac{1}{4},\frac{1}{2}] \cup [\frac{3}{4},1]\}$ 也是 [0,1] 上的一個劃分。 任給兩個劃分 $\overline{A}$ 和 $\overline{B}$，令 $\overline{A}\vee\overline{B}$ 為由下式定義的劃分

\begin{displaymath} \overline{A} \vee \overline{B} = \{ A\cap B : A \in \overline{A} , B \in \overline{B}\} \end{displaymath}


由此，我們則有 $f^{-1}(\overline{A})\vee\overline{A} =\{[0,\frac{1}{4}],[\frac{1}{4},\frac{1}{2}, [\frac{1}{2},\frac{3}{4}],[\frac{3}{4},1]\}$ 如此這般下去，我們會有

\begin{displaymath} \bigvee_{i=0}^{n-1} f^{-1}(\overline{A}) =\{ [\frac{i-1}{2^n},\frac{i}{2^n}] : i=1,\cdots,2^n\} \end{displaymath}


的劃分，這個劃分裡的每個區間 $[\frac{i-1}{2^n},\frac{i}{2^n}]$ 都有 2-n 的 Lebesgue 概率測度。 事實上，它和旋轉硬幣 n 次那個樣本空間裡的 2n 個基本事件是一一對應的。 拿 n=3 其中的一個簡單情況來看。把 $[\frac{3}{8},\frac{4}{8}]$ 這個區間左端的 $\frac{3}{8}$ 寫成

\begin{displaymath} \frac{3}{8}=\frac{0}{2}+\frac{1}{2^2}+\frac{1}{2^3} \end{displaymath}


然後將 $[\frac{3}{8},\frac{4}{8}]$ 這個區間和 011（第一次反面，第二次正面，第三次反面）對應。一般來說，我們可以把 $[\frac{i-1}{2^n},\frac{i}{2^n}]$ 這個區間左端的 $\frac{i-1}{2^n}$ 寫成

\begin{displaymath} \frac{i-1}{2^n}=\frac{a_1}{2}+\frac{a_2}{2^2}+\cdots+\frac{a_n}{2^n} \end{displaymath}


其中 ak=0 或 1, k=1,…,n。這個區間對應的是旋轉硬幣 n 次， 出現 $a_1 a_2\cdots a_n$ 的基本事件。 總的來說，旋轉硬幣 n 次，2n 個基本事件， 大家的機率都是 2-n 的樣本空間，拿 $f(x)=2x \pmod{1}$ 和劃分 $\overline{A}=\{ [0,\frac{1}{2}],[\frac{1}{2},1]\}$ 來描述， 則是：拿劃分 $\bigvee_{i=0}^{n-1} f^{-1}(\overline{A})$ 裡的 2n 個元素 $[\frac{i-1}{2^n},\frac{i}{2^n}]$ 做基本事件， 大家的 Lebesgue 概率測度都是 2-n 的樣本空間。 「已知旋轉硬幣第一次，第二次，…，第 n-1 次的結果， 那麼第 n 次會是正面或反面的不確定度是多少？」 的這一問題，拿 $f(x)=2x \pmod{1}$ 和劃分 $\overline{A}=\{ [0,\frac{1}{2}],[\frac{1}{2},1]\}$ 來描述， 事實上是在問：已知 x,…,fn-1(x) 在劃分 $\overline{A}$ 裡的位置，那麼 fn(x) 會在 $[0,\frac{1}{2}]$ 裡 或在 $[\frac{1}{2},1]$ 裡的不確定度是多少呢？ 讓我們來看 n=4 這個特殊情形。比如說我們已知前三次的結果， 它們是 101（第一次正面，第二次反面，第三次正面），這在 $\bigvee_{i=0}^{2} f^{-i}(\overline{A})$ 中所對應的區間是 $[\frac{5}{2^3},\frac{6}{2^3}]$，因為

\begin{displaymath} \frac{5}{2^3}=\frac{1}{2}+\frac{0}{2^2}+\frac{1}{2^3} \end{displaymath}


仔細的看，這個間區事實上是， $[\frac{1}{2},1]$ 和 $f^{-1}([0,\frac{1}{2}])=$ $[0,\frac{1}{4}]\cup [\frac{1}{2},\frac{3}{4}]$ 以及 $f^{-2}([\frac{1}{2},1])=[\frac{1}{8},\frac{1}{4}]$ $\cup [\frac{3}{8},\frac{1}{2}] \cup [\frac{5}{8},\frac{3}{4}]$ $\cup [\frac{7}{8},1]$ 的交集，也就是說

\begin{displaymath}[\frac{5}{2^3},\frac{6}{2^3}] =[\frac{1}{2},1]\cap f^{-1}([0,\frac{1}{2}])\cap f^{-2S}([\frac{1}{2},1]) \end{displaymath}


元素x在這交集所代表的意義是： $x \in [\frac{1}{2},1],f(x)\in [0,\frac{1}{2}]$ 和 $f^2(x)\in [\frac{1}{2},1]$。 一般說來，已知前三次旋轉硬幣的結果相當於已知 x,f(x),f2(x) 在劃分 $\overline{A}=\{ [0,\frac{1}{2}],[\frac{1}{2},1]\}$ 中的位置。 問第四次是正面還是反面的不確定度，相當於問 f3(x) 究竟是在 $[0,\frac{1}{2}]$ 中還是在 $[\frac{1}{2},1]$ 中的不確定度。 已知 $x,f(x),\cdots,f^{n-1}(x)$ 在那裡，問 fn(x) 在那裡的不確定度， 當 n 趨近於無窮大時的變化就是我們在這一節要談的 Kolmogorov 熵。 我們將把我們的著眼點放在一般的概率測度空間 (Probability measure space) 和定義在它上面的可測變換 (measurable function)。 設 $(X,\Sigma,\mu)$ 為一概率測度空間。即 X 為一集合， Σ 為 X 上的一些子集合所構成的一個 $\sigma-$代數， μ 為 Σ 上的概率測度，也就是說 $\mu(X)=1$。 假設 $f:X \longrightarrow X$ 為一個可測變換。 這是指，Σ 中每個元素的逆像 f-1(A) 仍在 σ 中。 我們任取 X 的一個有限劃分 (finite partition) $\overline{A}=\{ A_1,\cdots$ ,Am} 即 $\overline{A}$ 中每個集合 Ai 屬於 Σ， 它們之間互不相交（交集的測度為 0）且聯集恰為 X。 這樣 $\overline{A}$ 可看成具有「基本事件」 A1,A2,…,Am 且有概率分布 $\mu(A_1)$,…,$\mu(A_m)$ 的一個有限樣本空間。這個樣本空間經常被稱為「試驗結果」。上節中談到，這個「試驗結果」的 Shannon 熵應為：

\begin{displaymath} H(\overline{A})=-\sum_{i=1}^{n} \mu(A_i) \log \mu (A_i) \end{displaymath}


對給定的 f，集族 $f^{-1}(\overline{A})$ $=\{(f^{-1}(A_1),\cdots,f^{-1}(A_m) \})$ 也可給出 X 的一個劃分。首先我們要提出這樣的問題： 在試驗結果 $\overline{A}=\{ A_1,\cdots,A_m \}$ 為已知的前提下，試驗結果 $f^{-1}(\overline{A})=\{f^{-1}(A_1),$$\cdots,$ f-1(An)} 的不確定度為多少？也就是說，我們欲知：已知 x 在 Ai 中， 問 f(x) 在何處的不確定度為多少？ 我們可以從條件概率的角度來探討之。為簡單起見， 設 n=3，即 $\overline{A}=\{ A_1,A_2,A_3 \}$。 假如，已知 x 在 A1 中我們來看 f(x) 在 A1,A2 或 A3 的概率為如何。 對 $i=1,2,3,f(x) \in A_i$，當且僅當 $x \in f^{-1}(A_i)$， 故 x 在 A1 中且 f(x) 在 Ai 中之集合為 $A_1 \cap f^{-1}(A_i)$， 因而其條件概率為 $\mu(A_1 \cap f^{-1}(A_i) )$ $ / \mu(A_1)$。 由 Shannon 熵的定義知，在 $x \in A_1$ 的條件下， f(x) 會在 A1，或 A2，或 A3 的不確度應為

\begin{displaymath} H_1= - \sum_{i=1}^{3} \frac{\mu(A_1 \cap f^{-1}(A_i))}{\mu(A_1)} \times \log{(\frac{A_1 \cap f^{-1}(A_i)}{\mu(A_1)})} \end{displaymath}


類似地，在 $x \in A_2$，或 $x \in A_3$ 的條件下，試驗 結果 $f^{-1}(\overline{A})= \{ f^{-1}(A_1),f^{-1}(A_2),f^{-1}(A_3)\}$ 的不確定度應分別為

\begin{displaymath} H_2= -\sum_{i=1}^{3}\frac{(A_2 \cap f^{-1}(A_i))}{\mu (A_2)} \times \log{\frac{\mu(A_2 \cap f^{-1}(A_i))}{\mu (A_2)}} \end{displaymath}


和

\begin{displaymath} H_3=-\sum_{i=1}^{3}\frac{\mu(A_3\cap f^{-1}(A_i))}{\mu(A_3)} \times \log{\frac{\mu(A_3 \cap f^{-1}(A_i))}{\mu (A_3)}} \end{displaymath}


由推導 Shannon 熵定義的條件(ii)易知， 在試驗結果 $\overline{A}=\{ A_1,A_2,A_3 \}$ 為已知的條件下， 試驗結果 $f^{-1}(\overline{A})= \{ f^{-1}(A_1),f^{-1}(A_2),f^{-1}(A_3)\}$的不確定度 $H(f^{-1}(\overline{A})\vert\overline{A})$ 為H1,H2,H3的加權和，即

\begin{eqnarray*} && H(f^{-1}(\overline{A})\vert\overline{A}) \\ &=& \sum_{i=1}... ...}(A_j)) \times \log{\frac{\mu(A_i \cap f^{-1}(A_j))}{\mu (A_i)}} \end{eqnarray*}


如法炮製，對一般的有限劃分 $\overline{A}=\{ A_1,\cdots,A_m \}$ 我們可得到所謂的「劃分 $f^{-1}(\overline{A})$ 關於劃分 $\overline{A}$ 的條件 shannon 熵」，

\begin{eqnarray*} && H(f^{-1}(\overline{A}\vert\overline{A})) \\ &=& -\sum_{j=1... ...(A_j)) \times \log{\frac{\mu(A_i \cap f^{-1}(A_j))}{\mu (A_i)}} \end{eqnarray*}


下面，我們來給出上述 $H(f^{-1}(\overline{A})\vert\overline{A})$ 的另一等價型式以便後面推廣。
命題2-1：


\begin{displaymath} H(f^{-1}(\overline{A})\vert\overline{A})= H(\overline{A}\vee f^{-1}(\overline{A}))-H(\overline{A}) \end{displaymath}


證明：


\begin{eqnarray*} && H(f^{-1}(\overline{A})\vert\overline{A}) \\ &=& -\sum_{i=1... ...mu(A_i)} \\ &=& H(\overline{A} \vee f^{-1}(\overline{A})) -H(A) \end{eqnarray*}

命題2-1在直觀上看也很顯然：試驗結果 $\overline{A} \vee f^{-1}(\overline{A})$ 的不確定度 $H(\overline{A}\vee f^{-1}(\overline{A}))$應為試驗結果$\overline{A}$ 的不確定度 $H(\overline{A})$在試驗結果$\overline{A}$為已知條件下， 試驗結果 $f^{-1}(\overline{A})$的不確定度 $H(f^{-1}(\overline{A})\vert\overline{A})$ 之和。 上述已知試驗結果$\overline{A}$，問試驗結果f-1(A)的不確定度， 相當於已知x在$\overline{A}$中的位置， 我們問f(x)在$\overline{A}$中的位置的不確定度。 已知 $x,f(x),\cdots,f^{n-1}(x)$在分劃$\overline{A}$中的位置， 問 fn(x) 在 $\overline{A}$中的位置的不確定度， 則相當於已知試驗結果 $\bigvee_{i=0}^{n-1}f^{-i}(\overline{A})$ $=\overline{A}\vee f^{-1}(\overline{A})\vee \cdots f^{-(n- 1)}(\overline{A})$ ，問試驗結果 $f^{-n}(\overline{A})$ 的不確定度。 Kolomogorov 熵基本上是在刻劃這個不確定度在當 n 趨近於無窮大時的漸近性質。 任給自然數n， $\bigvee_{i=0}^{n-1}f^{-i}(\overline{A})$ 和 $f^{-n}(\overline{A})$ 都是 X 的有限劃分。 在已知試驗結果， $\bigvee_{i=0}^{n-1}f^{-i}(\overline{A})$ 的條件下， 試驗結果 $f^{-n}(\overline{A})$ 的不確定度， 實際上是劃分 $f^{-n}(\overline{A})$ 的條件 Shannon 熵，它是

\begin{eqnarray*} && H(f^{-n}(\overline{A})\vert \bigvee_{i=0}^{n-1} f^{-i}(\ove... ...f^{-i}(\overline{A}))-H(\bigvee_{i=0}^{n-1}f^{-i}(\overline{A})) \end{eqnarray*}


定義2-2：
設 $\overline{A}=\{ A_1,\cdots,A_m \}$為 X的有限劃分，則可測變換 $f:X \rightarrow X$關於$\overline{A}$ 的熵定義為

\begin{displaymath} h_{\mu}(f,\overline{A})= \lim_{n \rightarrow \infty} \mbox{s... ...(\overline{A}) \vert \bigvee_{i=0}^{n-1} f^{-i}(\overline{A})) \end{displaymath}


定義2-3：
設 (X,Σ,μ) 為一概率空間， $f:X \rightarrow X$ 為一可測變換， 則 f 的 Kolomogorov 熵定義為

\begin{displaymath} h_{\mu}(f)=\sup\{h_\mu(f,\overline{A}):\overline{A} \mbox{{\... ....1pt{\fontfamily{cwM0}\fontseries{m}\selectfont \char 125}} \} \end{displaymath}


對一般的可測變換 $f:X \rightarrow X$， 上述定義2-2中的上極限符號不能改為極限符號。 但對遍歷理論中所研究的一類重要可測變換-保測變換 (measure preserving transformation)我們可以證明極限 $\lim_{n \rightarrow \infty} H(f^{-n}(\overline{A})\vert\bigvee_{i=1}^{n-1} f^{-i}(\overline{A})$ 確實存在並有一另一種等價定義。該定義顯然不及前者直觀易懂， 但它卻給出了計算上的許多方便。所謂保測變換是指 $f:X \rightarrow X$， 任給 $A \in \Sigma$, $f^{-i}(A) \in \Sigma $ 且有

\begin{displaymath} \mu(f^{-1}(A))=\mu(A) \end{displaymath}


定義2-2：
設 $\overline{A}=\{ A_1,\cdots,A_m \}$ 為 X 的有限劃分， 則保測變換 $f:X \rightarrow X$關於$\overline{A}$的熵定義為

\begin{displaymath} h_{\mu}(f,\overline{A})=\lim_{n \rightarrow \infty } \frac{1}{n} H(\bigvee_{i=0}^{n-1}f^{-i}(\overline{A})) \end{displaymath}


在證明此定義合理，且與定義2-2等價之前，我們首先注意到如下的事實： 若f為保測變換，則 $H(f^{-1}(\overline{A}))=H(A)$ 這由條件 $\mu(f^{-1}(A))=\mu(A)$易見。 若$\overline{C}$和$\overline{D}$為X的兩個有限劃分， 我們記 $\overline{C} \leq \overline{D}$，若 $\overline{C}$的每一元素是$\overline{D}$中某些元素之聯(Union) (即$\overline{D}$是$\overline{C}$的一個細分(refinement)) 我們需要下列引理，其證明稍後給出。
引理2-4：
若 $\overline{C} \leq \overline{D}$， 則 $H(\overline{A}\vert\overline{C}) \geq H(\overline{A}\vert\overline{D})$
現在可以敘述並證明我們的等價定理了。
定理2-5：
若 $f:X \rightarrow X$ 為保測變換，則對 X 的任一劃分 $\overline{A}$

\begin{displaymath} \lim_{n \rightarrow \infty} H(f^{-n}(\overline{A})\vert \big... ...\infty } \frac{1}{n}H(\bigvee_{i=0}^{n-1}f^{-i}(\overline{A})) \end{displaymath}



證明：
n=1，則

\begin{eqnarray*} &&H(f^{-1}(\overline{A})\vert\overline{A}) \\ &=&H(f^{-1}(\ov... ...(\overline{A})) \\ &=&H(\overline{A}\vert f^{-1}(\overline{A})) \end{eqnarray*}


當 n=2 時，

\begin{eqnarray*} &&H(f^{-2}(\overline{A})\vert\overline{A}\vee f^{-1}(\overline... ...verline{A} \vert f^{-2}(\overline{A}) \vee f^{-1}(\overline{A})) \end{eqnarray*}


用歸納法易證，一般地有

\begin{displaymath} H(f^{-n}(A)\vert \bigvee_{i=0}^{n-1} f^{-i}(\overline{A})) =H(\overline{A}\vert \bigvee_{i=0}^{n} f^{-i} (\overline{A})) \end{displaymath}


由上述引理2-4，故極限存在。從而，定義2-2中的極限實際上存在。 另一方面，對 i=1,2,…,n-1，由

\begin{displaymath} H(f^{-1}(\overline{A})\vert \bigvee_{i=0}^{i-1} f^{-j}(\over... ...-j}(\overline{A})) -H(\bigvee_{j=0}^{i-1}f^{-j}(\overline{A})) \end{displaymath}


各式相加，我們有

\begin{eqnarray*} &&H(\bigvee_{i=0}^{n-1} f^{-1}(\overline{A})) \\ &=& H(\overl... ...}^{n}H(\overline{A}\vert\bigvee_{j=0}^{i-1}f^{-j}(\overline{A})) \end{eqnarray*}


故有

\begin{displaymath}\frac{1}{n}H\bigvee_{i=0}^{n-1} f^{-i}(\overline{A})) = \frac... ...n-1}H(\overline{A}\vert\bigvee_{i=0}^{i} f^{-j}(\overline{A})) \end{displaymath}


借用初等微積分的已知結果： $\lim_{n \rightarrow \infty} a_n = L \Rightarrow \lim_{n \rightarrow \infty} \frac{1}{n} \sum_{i=0}^{n-1} a_i =L$，我們得到

\begin{eqnarray*} && \lim_{n \rightarrow \infty} \frac{1}{n}H(\bigvee_{i=0}^{n-1... ...^{-n}(\overline{A})\vert\bigvee_{i=0}^{n-1}f^{-i}(\overline{A})) \end{eqnarray*}


現在我們來證明引理2-4。 設 $\overline{A}=\{A_i \}$, $\overline{C}=\{C_j\}$, $\overline{D}=\{D_k\}$， 我們要證

\begin{eqnarray*} && -\sum_{j}\sum_{i} \mu (C_j)\frac{\mu(A_i \cap C_j)}{\mu(C_j... ...k)}{\mu(D_k)} \times \log{\frac{\mu(A_i \cap D_k)}{\mu(D_k)}}\\ \end{eqnarray*}


只須證明對每一 i 和 j

\begin{eqnarray*} &&\mu(C_j)\frac{\mu(A_i \cap C_j)}{C_j} \log{\frac{\mu(A_i \ca... ..._i \cap D_k)}{\mu(D_k)} \log{\frac{\mu(A_i \cap D_k)}{\mu(D_k)}} \end{eqnarray*}


令 $\phi(x)=x\log{x}$, $\phi(0)=0$ 則上式為

\begin{eqnarray*} \phi(\frac{\mu(A_i\cap C_j)}{\mu(C_j)}) \leq \sum_{k} \frac{\mu(C_j \cap D_k)}{\mu(C_j)} \phi(\frac{\mu(A_i \cap D_k)}{\mu(D_k)}) \end{eqnarray*}


由於 $\phi$ 是凸函數(這由 $\phi ''(x)=\frac{1}{x}>0$ 可知) 和假設 $\overline{C} \leq \overline{D}$，易知

\begin{eqnarray*} &&\sum_{k}\frac{\mu(C_j\cap D_k)}{\mu(C_j)} \phi(\frac{\mu(A_i... ..._k)}{\mu(D_k)}) \\ &=& \phi(\frac{\mu(A_i \cap C_j)}{\mu(C_j)}) \end{eqnarray*}


即我們證明了 $H(\overline{A}\vert\overline{C}) \geq H(\overline{A}\vert\overline{D})$ 歷史上，引進 Kolmogorov 熵概念的主要動力是關於概率空間保測變換之間共軛關係的不變量的研究。 設 $(X_{1},\Sigma_{1},\mu_{1})$ 和 $(X_2,\Sigma_2,\mu_2)$ 為兩個概率空間， $T_1: X_1 \rightarrow X_1$和 $T_2: X_2 \rightarrow X_2$ 為保測變換。 我們說 T1 和 T2 共軛 (conjugate) 是指存在一個保測同構 $\phi :$ $(X_2,\Sigma_2,\mu_2)$ $\rightarrow$ $(X_1,\Sigma_1,\mu_1)$ 使得 $\phi \circ T_2^{-1}= T_1^{-1}\circ \phi$。 我們稱一個數量為共軛保測變換的「不變量 (invariance)」 是指二個保測變換若是共軛，這個數量一定一樣。 這個數量若不一樣，這兩個保測變換一定不共軛。 共軛的保測變換具有同樣的遍歷性質。 我們若能找到關於共軛保測變換的不變量，我們就可從本質上刻劃不同共軛類保測變換的特徵：Kolmogorov 熵就是這樣的一個重要的不變量。 早在1943年，人們就知道 Bernoulli 的 ( $\frac{1}{2},\frac{1}{2}$) -雙邊移位算子 (two side shift) 和 ( $\frac{1}{3},\frac{1}{3},\frac{1}{3}$)- 雙邊移位算子都具有可數個 Lebesgue 譜點，因而是譜同構的，但不知道它們是否共軛。 直到1958年才由 Kolmogorov 證明了它們分別具有 $\log 2$和 $\log 3$ 的 Kolmogorov 熵，故非共軛。從而消除了遍歷理論這個重大懸念，並開創了一個嶄新的研究領域。 我們這裡介紹的 Kolmogorov 熵的概念是由 Kolmogorov 的學生 Sinai 在1959年改進的，和 Kolmogorov 1958年給出的原始定義稍有不同。 		   



上頁　1│2│3│4　次頁
回頁首
 
（若有指正、疑問……，可以在此 留言 或 寫信 給我們。）
EpisteMath

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強 ∕ 繪圖：簡立欣最後修改日期：5/6/2002
at

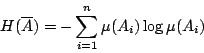
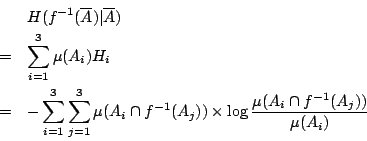
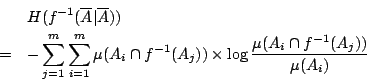
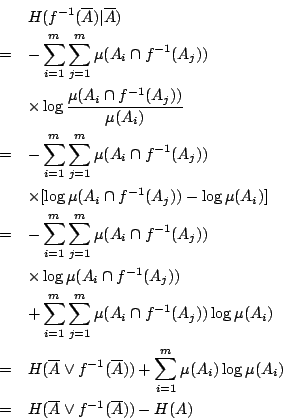
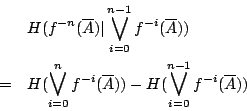
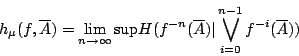
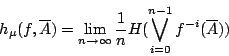
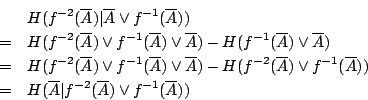
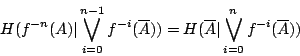
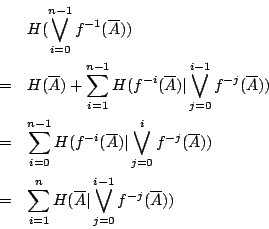
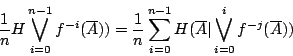
No comments:

Post a Comment