Friday, May 23, 2014

生物分子系统由泊松方程或者泊松-波尔兹曼方程 , 泊鬆發現拉普拉斯方程只在固體之外是正確的。可變密度的質量 曲面電勢Ψ的泊松方程，顯示對於電荷密度ρe在特定點的依賴性

phymath999: "波尔兹曼分布定律"，适用于能级为非简并的可 ...

phymath999.blogspot.com/2013/08/gij-gi.html - 轉為繁體網頁
2013年8月11日 - 当前位置: 7 统计热力学基础-> 7.3 波尔兹曼分布律与粒子配分函数 -> 7.3.1 波 ..... qm01 phymath01 算子01 矩陣01 有時候用矩陣形式寫下特徵值方程是不 .... 泊松分布坚持的力量贝叶斯意义下，先验分布是高斯或者泊松分布，后验 ...
  • [PDF]

    RNA 分子折叠的统计力学 - University of Missouri

    vfold.missouri.edu/paps/review.05Phys.pdf

    轉為繁體網頁
    由 陈世杰 著作 - ‎相關文章
    子执行着从遗传信息的传递、储存到对蛋白质合成 .... 的一些基团可带有极化偶极子或感应极化偶极子. ・. 701 ..... 泊松—玻尔兹曼（Poisson r Boltzmann，PB）理论和.

  • 张显文 - 华中科技大学数学与统计学院

    maths.hust.edu.cn › 首页 › 党务人事 › 师资队伍

    轉為繁體網頁
    Vlasov-Poisson系统. 中子输运 ... 华中理工大学科学研究基金: 微分算子的奇异连续谱(1999.1-2000.12). 1万元. ... 张显文：《非线性波尔兹曼方程》（讲义）. 待出版.
  • [PDF]

    TREECODE ALGORITHM FOR PAIRWISE ...

    math.sjtu.edu.cn/faculty/xuzl/.../Haizhao_thesis_final.pdf

    轉為繁體網頁
    计算。在隐式模型中，生物分子系统由泊松方程或者泊松-波尔兹曼方程所描述。当 ... 子系统中不存在自由电子时，可以去掉泊松-波尔兹曼方程中的波尔兹曼项，从而得.




    • 他著名的對勢的拉普拉斯的偏微分方程的二階修正：
    \nabla^2 \phi = - 4 \pi \rho \;
    今天以他命名為泊松方程或者叫位勢論方程，最初發表於Bulletin de in société philomatique (1813年)。如果給定點的函數ρ = 0，我們得到了拉普拉斯方程：
    \nabla^2 \phi = 0 \;
    1812年，泊鬆發現拉普拉斯方程只在固體之外是正確的。可變密度的質量的情況的嚴格證明由高斯於1839年第一次給出。兩個方程在向量代數中都​​有對應。從給定其梯度的散度ρ(x, y, z) 得到的標量場導出三維空間的泊松方程：
    \nabla^2 \phi = \rho (x, y, z) \;
    例如，對於曲面電勢Ψ的泊松方程，顯示對於電荷密度ρe在特定點的依賴性：
    \nabla^2 \Psi = {\partial ^2 \Psi\over \partial x^2 } + {\partial ^2 \Psi\over \partial y^2 } + {\partial ^2 \Psi\over \partial z^2 } = - {\rho_{e} \over \varepsilon \varepsilon_{0}} \;
    流體中的電荷分佈是未知的，我們必須使用泊松-波爾茲曼方程：
    \nabla^2 \Psi = {n_{0} e \over \varepsilon \varepsilon_{0}} \left( e^{e\Psi (x,y,z)/k_{B}T} - e^{-e\Psi (x,y,z)/ k_{B}T} \right), \;
    它在多數情形下無法求得解析解，但是對於特殊情況可以。在極坐標下，泊松－波爾茲曼方程為：
    {1\over r^{2}} {d\over dr} \left( r^{2} {d\Psi \over dr} \right) = {n_{0} e \over \varepsilon \varepsilon_{0}} \left( e^{e\Psi (r) / k_{B}T} - e^{-e\Psi (r) / k_{B}T} \right) \;
    它也不能解析求解。如果場 φ 不是一個標量，泊松方程是正確的，例如在四維閔可夫斯基空間：
    \square \phi_{ik} = \rho (x, y, z, ct) \; .
    若ρ(x, y, z)是連續函數而若對於r→∞ （或者當一個點“移向”無窮遠），函數φ趨向0足夠快，泊松方程的一個解是函數ρ(x, y, z)的牛頓勢：
    \phi_M = - {1\over 4 \pi} \int {\rho (x, y, z)\, dv \over r} \;
    其中r為具有體積dv的元和點M的距離。
    積分跑遍整個空間。泊松積分可用於求解拉普拉斯方程的狄利克雷（Dirichlet）問題的格林函數，如果圓是所求區域：
    \phi(\xi,\eta) = {1\over 4 \pi} \int _0^{2\pi} {R^2 - \rho^2\over R^2 + \rho^2 - 2R \rho \cos (\psi - \chi) } \phi (\chi)\, d \chi \;
    其中
    \xi = \rho \cos \psi, \;
    \quad \eta = \rho \sin \psi. \;
    φ(χ)在圓圈上給定，定義了拉普拉斯方程要求的函數φ的邊界條件。
    同樣，我們可以定義空間拉普拉斯方程∇2 φ = 0的迪力克雷問題的格林函數，如果求解的區域是半徑為R的球。這次，格林函數為：
    G(x,y,z;\xi,\eta,\zeta) = {1\over r} - {R\over r_1 \rho} \; ,
    其中
    \rho = \sqrt {\xi^2 + \eta^2 + \zeta^2}
    是點(ξ, η, ζ)到球心的距離；r是點(x, y, z)和(ξ, η, ζ)的距離；r1是點(x, y, z)和點(Rξ/ρ, Rη/ρ, Rζ/ρ)的距離，對於點(ξ, η, ζ)對稱。
    泊松積分現在形為：
    \phi(\xi, \eta, \zeta) = {1\over 4 \pi} \int\!\!\!\int_S {R^2 - \rho^2 \over R r^3} \phi\, ds \; .
    泊鬆在該主題上的最重要的兩個備忘錄是《關於類球體的引力》（Sur l'attraction des sphéroides） (Connaiss. ft. temps, 1829年)和《關於均勻橢球體的引力》（Sur l'attraction d'un ellipsoide homogène） (Mim. ft. l'acad., 1835年)。當結束我們從他的物理備忘錄的節選時，我們來提一下他的波動理論備忘錄(Mém. ft. l'acad., 1825年)。

    純數學[编辑]

    在純數學方面，他最著名的工作是他在定積分上的一系列備忘錄，和他關於傅立葉級數的討論，它為狄利克雷和黎曼在同一主題上的經典研究鋪平了道路；這些可以在理工學院從1813年到1823年的《期刊》中找到。他也研究了傅立葉積分。此外，我們也可以提一下他關於變分法的文章（Mem. de l'acad., 1833年），以及他在觀測平均值的概率方面的備忘錄（Connaiss . d. temps, 1827年, &c）。 概率論中的泊松分佈以他命名。
    在他的《力學專論》（Traité de mécanique） (2 vols. 8vo, 1811年及1833年)中，他採用拉普拉斯和拉格朗日的風格寫作，是一部標準的著作，他展示了很多新的技巧，例如衝量坐標的顯式使用：
    p_i = {\partial T\over {\partial \dot q_i}} \;
    它影響了哈密爾頓和雅可比的工作。

    at

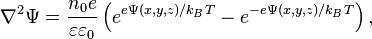
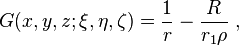
    No comments:

    Post a Comment