地球的位移矢量对时间的二阶导数和圆周轨道的曲率的平方成正比
如果用几何语言，我们可以说点质量或点电荷的等位面上的势和该等位面的曲率的平方根成正比
早在17世紀，伽利略已利用物體從斜面滾下不同的距離所需要的時間，去證明物體於地球上的自由下落的加速度是一個常量；另外，伽利略亦發現單擺的週期只與擺長有關，而與擺錘的質料無關。稍後的牛頓則做了兩個等長而同形狀的單擺，其中一個的擺錘是用金做的；而另一個擺錘用等重的銀、鉛、玻璃、沙等不同物料製成。而牛頓在多次實驗均未能觀察到它們之間的週期差異。
從牛頓力學來說，質量本身被付予兩種不同的意義：一個從動力學方程式（牛頓第二定律）引入：
是指慣性質量，代表著物體運動的慣性，即是物體抵抗運動變化的程度；另一方面，從牛頓萬有引力定律：
是代表物體引力大小的一個參數，稱作引力質量。引力时空是弯曲的吗？
引力时空是弯曲的吗？
王令隽 2011年一月
近代物理的诸多革命性的理论中，最为令人费解而感到莫测高深的概念之一，是引力时空弯曲的概念。我把“引力时空弯曲”叫做“概念”而不是“理论”，是因为没有一个系统的理论证明这一概念。
这可能会让读者们感到惶惑：难道爱因斯坦的广义相对论不是一个证明这一概念的系统理论吗？广义相对论的数学基础是黎曼几何 — 曲面几何。爱因斯坦的引力场方程就是：爱因斯坦张量正比于能动量张量。而爱因斯坦张量就是从时空曲率张量收缩而成的。既然引力作用可以用黎曼空间中的场方程完全表述，那么就可以认为引力本质上是几何。难道这还不能说明引力时空是弯曲的吗？
不能。在探讨这个问题之先，我要特别说明，以下的讨论不挑战爱因斯坦引力场方程的正确性（当然也不确认它的正确性）。即是说，引力时空是否弯曲的概念和爱因斯坦引力场方程是否正确是完全不相关的两个问题。即使爱因斯坦引力场方程成立，也并不能证明引力时空是弯曲的。
一。运动轨迹的弯曲不意味着时空的弯曲
物体的运动轨迹可以是直线，也可以是曲线。垂直落下的物体的运动轨迹是一条直线；炮弹的运动轨迹是抛物线，行星的运动轨迹是圆或椭圆。描绘这些不同的曲线方程就是运动方程 – 规定某一物体所在的时空坐标关系的方程。显然，运动方程式中所规定的时空关系仅仅是某一物体可能经过的时空坐标点的关系，而不影响整个宇宙的时空结构。一只蝴蝶在空中翻飞，他所经过的时空坐标构成非常复杂而美丽的曲线，但这决不意味着整个世界的时空被这只蝴蝶搞弯曲了。这只蝴蝶可能自己觉得天翻地覆，如果宇宙间只有这只蝴蝶并且它服膺时空弯曲论，它也许可以认为时空的结构不仅是弯曲的而且时空还会翻跟斗玩杂技。可是宇宙间除了这只蝴蝶外还有追逐他的螳螂，黄雀和其他万事万物。这时空是大家的而不是蝴蝶那厮可以独占的，时空结构岂可由它一言而断曲直？
在经典力学里，运动方程就是牛顿第二定律。万有引力场中的运动方程规定了物体的运动轨迹必须是圆锥曲线。其中最简单的就是圆。地球的运动轨道就差不多是围绕太阳的一个圆。因为圆的曲率是半径的倒数，所以地球的运动方程可以表述为：地球的加速度和圆周轨道的曲率的平方成正比。这样的表述就把引力描述成了某种空间的几何特性。但是这种几何特性只属于行星的轨道，和宇宙空间的性质毫不相干。高能的宇宙射线中的带电粒子穿越太阳系，它的轨道可以是直线，双曲线或抛物线，它所感受到的时空性质和地球的轨道曲率毫无关系。所以，地球的运动方程的空间性质和轨道的弯曲决不意味着宇宙空间的弯曲。还是那句话，时空是大家的，不是只属于地球的。
如果我们选择以太阳为中心的球面坐标系而不是笛卡儿坐标系，则地球和其他行星的运动方程可以表述为：太阳系中的任何物体的加速度和它所在的球坐标面的曲率成正比。这样，可不可以把引力看成是空间本身的某种几何性质呢？万有引力和行星轨道可以用球面坐标来描述，可不可以认为是空间弯曲的证据呢？
不可以！我们选择球面坐标系，只是选择了一种较为方便的坐标系统，并没有改变空间的性质。我们同样可以选择笛卡儿坐标系来有效地描述行星的运动。难道空间的曲直会取决于我们对坐标系的选择？这符合相对性原理吗？天文学家几百年前就开始用球面坐标系来描述天体的运动，从来没有人认为一旦采用了球面坐标，宇宙空间就弯曲了。
加速度是位移矢量对时间的二阶导数，所以引力场中物体的运动方程又可以表述为：地球的位移矢量对时间的二阶导数和圆周轨道的曲率的平方成正比。这种表述更符合相对论理论的张量语言。但并没有改变问题的物理实质，也不能改变宇宙的时空性质。
其实，除了引力场中的物体运动方程可以用几何语言来表述，其他运动方程也可以用几何语言表述。比如说，圆周运动不一定非要引力不可。汽车轮子，机器的飞轮，田径运动员的铁饼，骑摩托车飞檐走壁的杂技演员，加速器里面旋转的电子等等的圆周运动都不是因引力造成的。用上述几何语言，圆周运动的方程可以表述为：位移矢量对时间的二阶导数和圆周轨道的曲率成正比，同时又和位移矢量对时间的一阶导数的平方成正比。注意这里不涉及任何万有引力常数或质量之类的东西，是完完全全的几何关系，而且适用于所有圆周运动。这种普适的几何关系甚至和长度与时间单位的选择无关。但是这种普适的圆周运动方程的几何表述丝毫不影响宇宙空间的平坦，均匀，各向同性的物理性质，丝毫不能使空间弯曲。因为这种几何关系所规定的，仅仅是某物体的运动轨迹的几何特性，而不是整个空间的几何特性。
有了对经典运动方程中的空间和时间变量的物理意义的正确理解，就不难理解广义相对论中运动方程的物理意义。在广义相对论中，运动方程就是黎曼空间中的短程线方程。这一短程线方程中的空间和时间变量只是受引力作用的物体所能经历的空间和时间坐标，而不是整个宇宙的空间和时间。短程线方程规定的时间和空间坐标的关系，只描述物体运动轨迹的几何性质，不描述宇宙空间的几何性质。这一点, 在弱引力场下对短程线作线性近似以后就看得更加清楚。此时短程线方程就直接过渡到经典的牛顿定律和运动方程。所以，广义相对论中的运动方程由黎曼空间的短程线方程描述，并不意味着宇宙空间是弯曲的，最多只意味着某物体在引力下的运动轨迹可能是弯曲的。
二。引力场方程本质上是运动方程的不同表述
人们相信引力使时空弯曲的另一个原因，是爱因斯坦的引力场方程中的爱因斯坦张量是由时空曲率张量收缩而成。这使爱因斯坦认为能动量张量造成了时空的弯曲，而时空的弯曲造成引力。这一观点很快被许多人接受而成为广义相对论理论界的流行看法。
爱因斯坦在建立场方程时，应该是从“能动量使空间弯曲”的猜想中得到灵感的。他根据这一猜想建立了广义相对论的引力场方程，这自然使人们相信引力使时空弯曲。从科学史和人文传记的角度看，这种猜想被接受是可以理解的。但从科学理论的严密性来考量，某种猜想或概念是否正确，不能仅看某一理论或观念形成的思想史，不能光看爱因斯坦从什么思想得到灵感，而要分析这一理论的物理意义。爱因斯坦有许多异乎寻常的思想，但不一定都对。有些被他自己否定了，比如万有斥力和宇宙项；有些被学界和它自己一起抛弃了，比如他的宇宙模型。为了了解爱因斯坦引力场方程的物理意义，我们还是从经典场论开始。
一个引力场既可以用场强来描述，也可以用它在空间各点的势能分布来描述。但这两种描述是等价的，同样有效的。场强是矢量，而势是标量。标量的数学处理通常比矢量的处理简单方便得多。所以只要有可能，我们通常先求得势。有了势，算出它的负梯度就是场强。算梯度是做微分，计算非常直截了当。
点质量或点电荷（或均匀的球形质量或球形电荷）的引力场或静电场十分简单，空间任何一点的势和从该点到球心的距离成反比。点质量或点电荷的等位面（或等势面）就是以其为中心的同心圆。如果用几何语言，我们可以说点质量或点电荷的等位面上的势和该等位面的曲率的平方根成正比。这种曲率并不是宇宙空间的属性，而只是等位面的属性。等位面的弯曲并不意味着空间的弯曲。我们在建立势的理论时是以一个平坦的刚性的均匀的各向同性的空间为前提的。描述势的空间分布的场方程和描述场强的空间分布的方程都能得到同样的运动方程，所以他们都是等效的。
如果质量或电荷不是静止的，而是随时间变动的，则场强的分布和势的分布会随时间而变动。等位面也会随时间而变动，形成波向外传播。因此，等位面的形状和位置会随时间而改变，移动。但是，这种变化并不是说整个空间在波动，在变化。描述真空中波动方程的前提也是一个平坦的刚性的均匀的各向同性的空间。
描述电磁场的理论非常成熟，非常精确。电磁场的场方程就是麦克斯韦的电磁场方程。波动方程既可以通过场强来描述，也可以通过标量电位和矢量磁势来描述。不同的数学表述方法并不改变它们所描述的同一物理现象。场方程和运动方程描述的是本质上同样的现象。这些方程中的空间和时间变量所代表的，都只是质量或电荷在引力场或电磁场中的运动轨迹的时空关系；或场强和势的空间分布和时变特性，根本不是宇宙时空的几何特性。
爱因斯坦的引力场方程中的时间和空间变量也是描述引力场的势的空间分布和时变特性的参数。这一点，在爱因斯坦场方程的线性近似中看的十分清楚：引力场的时空度规元素中的引力修正量h在线性近似下过渡到经典的引力势。爱因斯坦场方程中规定的时空关系和曲面几何特性，可以联系于等位面的弯曲的几何特性和时变特性，但不是宇宙时空的几何特性。
有人会说，这只不过是一个观点问题。你可以认为时空是平坦的，弯曲的只是场强曲线和等位面；我也可以认为弯曲的是时间和空间本身。比如地球的圆周轨道，既可以认为是平坦空间中的曲线，也可以认为是弯曲的球面空间中的“直线”（短程线）。两种不同的观点得到的数学结果是一样的。既然引力作用可以用黎曼空间中的场方程完全表述，那么就可以认为时空是弯曲的，引力本质上是几何。
这种看法经不起逻辑推敲。我们必须认识到，时间和空间是属于宇宙间的一切自然现象的，而不是仅仅属于引力场的。在同一时空中，既有引力作用，也有电磁作用和核作用。让我们考虑一个很普通而又极简单的情形：在引力场中的电磁波。引力场由爱因斯坦场方程描述，电磁波由麦克斯韦场方程描述。爱因斯坦场方程的度规张量是弯曲的，而麦克斯韦方程的度规张量是平坦的闵可夫斯基度规。那时空到底是听爱因斯坦的还是听麦克斯韦的？在决定公共的时空特性时，我们有什么理由赋予引力作用以独断专行的特权，而令所有其他作用力处于听命的被奴役的地位？
麦克斯韦方程组中的时间和空间变量是经典的平坦时空，麦克斯韦的经典电动力学是经过无数宏观实验和工程实践检验过，现在还每日每时被检验的不容置疑的理论。如果时间和空间被弯曲了，则整个麦克斯韦方程组都要被扭曲了。即是说，时空弯曲的理论本质上决定了引力和其他作用力的耦合，而且这种耦合是单向的。质量使时空弯曲的理论是对电磁理论和核理论的根本修正。到现在为止，我们没有找到万有引力和其他相互作用力耦合的任何证据。把引力和其他相互作用统一的理论尝试也是失败的。万有引力是我们知道的所有作用力中最弱的一种。以万有引力相互作用而决定整个空间的曲直而左右其他作用力，不仅霸道，也太不自量力。
综上所述，虽然爱因斯坦张量是由时空曲率张量收缩而成，并根据此一张量建立引力场方程，但是爱因斯坦引力场方程本质上和运动方程一样，描述的仍然是引力场中的物体运动的轨迹和引力场结构。这些方程中的时间和空间关系，规定的是引力场中物体的运动轨迹，场强曲线和等位面的几何特性，而不是整个宇宙空间的特性。
三。时空弯曲的概念不是从黎曼几何推导出来的
如果爱因斯坦场方程仅仅是对牛顿引力方程的修正，其意义便不足以惊天动地。要建立一个伟大的理论，做出一些伟大的预言，必须往场方程里注入一些新的概念，新的假设。这里最重要的概念或假设，就是将引力场中的时间定义为时空间隔ds. 这一概念是从狭义相对论中直接“推广”而来。所以爱因斯坦的引力理论又叫做广义相对论。要注意的是，这种相对论的时间概念不是从爱因斯坦的引力场方程或黎曼几何中推导出来的，而是从狭义相对论的概念推广而来，从外面注入引力场理论的。
即使广义相对论最坚定的支持者也知道，爱因斯坦场方程的黎曼几何表述和运动方程的短程线表述，并不是时空弯曲的直接证明。比如，奥哈尼安（Hans Ohanian）在他的“Gravitation and Spacetime （1976年版）”一书中就强调，光线在引力场中的弯曲和引力场中的时间延缓才是时空弯曲的直接证据(Direct Evidence)。这一说法有些道理，因为这两个预言如果被实验证实，至少可以说明因为引力的存在影响电磁波的传播，因此可以说，麦克斯韦方程组受到了影响。
值得特别强调的是，奥哈尼安这里所说的，也仅仅是证据(Evidence)，而不是证明(Proof)。因为在数理逻辑上，爱因斯坦场方程既不能得到引力使光线弯曲的结果，也不能得到引力使时间延缓的结论。要得到这两个结论，需要外加几个假定：一）爱因斯坦引力场方程适用于电磁场；二）引力场方程中的物体的动量适用于电磁场的动量；三）引力场中的时间间隔的量度不是时间变量的微分dt，而是时空间隔的微分ds，而时空间隔是由四维时空矢量与度规张量的内积收缩而成，既包含时间微分dt，也包含空间微分dx。这一时空间隔ds 定义为“固有时间”(Proper time)。这些假定不能从黎曼几何或者爱因斯坦引力场方程中“推导”出来，而只能被“定义”，被“引进”来，与爱因斯坦场方程一起构成广义相对论的主要内容。如果这些假定成立，则光线会被引力弯曲，时间会被引力延缓；如果这些假定不成立，或引力不存在，光线也可能会被其他因素弯曲，时间也可能被狭义相对论效应延缓。所以即使测量到了引力场中光线的弯曲和时间的延缓，也只能作为广义相对论的“证据”而不是“证明”，更不能作为时空弯曲的“证明”。
对于第一个假定的实验检验是光线在引力场中的弯曲。爱丁顿的实验因此成了使广义相对论得到学界承认的历史性实验。但是这个实验是极不可靠的，因为光线掠过太阳表面会被一万公里厚的，呈球面弯曲的，密度不均匀的，非常活跃的色球面和日冕所折射而弯曲。根据实验物理的原则，要得到光线因引力而弯曲的实验证据，至少应该在总的观测数据中减除因为色球和日冕折射而造成的弯曲并剔除其他可能的原因，或者找一个没有外层大气的天体（比如月亮）来做实验。否则这种所谓的“实验证据”就是假的。爱丁顿的成名其实是媒体炒作的结果。
至于第二个假定，是爱因斯坦从狭义相对论中时间的相对性推广而来的。狭义相对论中的时间相对性会导致“钟佯谬”，因而可以通过逻辑证伪（细节请参看拙作“检验钟佯谬的对称试验””Symmetrical Experiments to Test Clock Paradox”, Ling Jun Wang, Physics and Modern Topics in Mechanical and Electrical Engineering, p 45, Ed., Nikos Mastorakis, World Scientific and Engineering Society Press, ISBN: 960-8052-10-6, July 1999.）。广义相对论的时间的相对性却不容易用逻辑来证伪，因为有引力的情形和没有引力的情形是不对称的，不可互易的。狭义相对论中，坐标系的运动是相对的，因而时间的延缓也是相对的；但在广义相对论中，引力的存在与否却不是相对的，而是绝对的，所以时间的延缓也是绝对的而不是相对的。这就使逻辑证伪比较困难，而实验检验变得异常重要了。
检验引力使时间延缓的最重要，也是最直接的实验是美国海军研究所的Hafele 和Keating 于1972年进行的原子钟环球实验。他们用飞机装上四个铯原子钟在约十公里的高度向东西两个方向飞行，然后比较这几个原子钟和地上的原子钟的快慢。因为这一实验涉及到因飞机运动造成的时间延缓和引力延缓的叠加，因此不能算是引力延缓的独立实验。另一方面，他们所使用的实验设备的精度根本不可能测量到如此小的时间延缓（在毫微秒的数量级）。 同时，他们用了特别的数据处理方法以凑出所期待的结果。对此我在“检验钟佯谬的对称试验”一文中有详尽的分析。
还有一种测量引力使时间延缓的方法，就是测量引力红移。理论计算表明，太阳的引力应该使太阳表面的原子谱线的频率比无穷远处的原子频谱的频率低大约百万分之二。这样大的引力红移应该是比较容易测量的，因为频谱分析是最为精确的实验测量手段之一。可是当人们认真地进行测量时，发现测量到的谱线红移和理论预言不符。于是人们解释说，这是因为在太阳的大气层里有强烈的气流，而气流中的分子的运动会因多普勒效应造成谱线红移。这种多普勒红移把引力红移掩盖了。不难想象，如果爱丁顿的太阳引力使光线弯曲的实验得不到他所预期的结果，他同样会解释为由于太阳色球面和日冕的折射而把引力效应掩盖了。后来，J.W Brault 和J.L. Snider 分别于1962年和1972年测量到了与理论期望相近的太阳红移数值，于是人们就认为这些数据是可靠的。至于太阳的大气层里的气流分子的运动的多普勒效应造成的谱线红移，当然就不得不被排除在外了。理由吗，找起来也方便，据说是因为这些钠和钾的谱线来自于光球面之外！这有点匪夷所思，因为“光球面”的定义就是太阳上发光的球面。光球面以外的部分是不发光的，怎么会有谱线呢？由此可见这一类实验解释的任意性，以及人们对待实验结果的选择性标准。一旦一个理论成为了流行的权威性理论，凡是印证它的实验都会被认为是可靠的实验证据，而和权威理论相悖的实验结果就会被认为是不可靠的。也因为如此，绝大多数科学家都知道厉害，凡是与权威理论不符合的结果索性不发表，以免影响到科研经费来源和学术名声。这样一来，支持权威理论的数据就越来越多，反面的数据即使不被驳倒也会被统计淹死。所以教科书上要列举一些支持理论的实验数据实在是太容易了。要揭露这些实验的错误，是非常吃力不讨好的事。只有你的分析无懈可击才有可能发表。有问题的实验实在太多了，你也驳不过来。经过了1958年大跃进运动的同胞们对这种情形应该非常熟悉。
其实要真想测量引力延缓，不必用飞机，只要在不同高度的实验室里放上一些原子钟，然后测量他们的时间差。因为这些钟都是静止的，所以不存在狭义相对论的时间延缓问题，因而是测量引力延缓的独立试验。另一方面，因为不用飞机，实验时间没有限制，可以通过长时间的积分增加信号。实验室的环境与稳定性控制也比飞机上要容易得多。中国的西康地区，峨眉山，华山，台湾的玉山等等，都可以进行这种实验测量。其实，在月亮上放置几个太阳能原子钟，也可以进行类似测量。欢迎有兴趣的朋友和我联系，讨论这一类实验的技术细节。
如果测量到了引力对原子钟快慢的影响，是否就意味着证实了，或间接印证了时空的弯曲？否！举个例子来说吧。以单摆控制快慢的钟的周期和引力加速度的平方成反比。同一个单摆钟放到月亮上，周期要延长到相当于地球上的周期的两倍半，所以登月运动员的步行动作有点像快镜头慢动作电影。但这并不意味着时空的弯曲。原子中的物理过程好像不应该受引力影响，但是原子钟毕竟是一台相当大的设备，其运行不仅取决于原子过程，也取决于其他附件的性能。我们无法排除这些因素受引力影响的可能性。举个例子，电子振荡器的固有频率决定于电感和电容，但是漏电阻和负载电阻会改变这一“固有频率”。没有阻尼的振荡电路是没有的。这种阻尼的量度叫作“品质因数”。石英振荡器的频率稳定，就是因为品质因素高，而原子钟的品质因素更高。但只要有负荷，品质因素就不可能无穷大，频率就有可能受外界条件影响。这种影响造成的钟表的固有频率的变化不能证明引力使时间延缓。
四。非欧几何的背景是平坦时空中的曲线坐标系
相信时空弯曲的朋友们还忘记了一个基本事实：所有曲面几何中的公式和方程式的推导与证明，都是在一个均匀平坦的欧几里得空间中得到的。也就是说，均匀的平坦的欧几里得空间是曲面几何的背景与本底。曲面几何只不过是用弯曲的坐标系代替平直正交的笛卡儿坐标系来描述同一个几何体，他并不改变空间本身的几何特性。球面坐标系和柱面坐标系被科学家用了几百年了，黎曼早在1854年就提出了黎曼几何，但是这种新的几何学不要求，也不意味着空间的弯曲。整个黎曼几何的演绎和推理，都以一个均匀平坦的欧几里得本底空间的存在为依据，否则，新的几何中的任何关系都不可能成立。
如果不相信，朋友们可以试试推导一下黎曼几何中最基本的一些关系，比如协变微分，度规联络，短程线方程和曲率等等。如果不假定一个均匀平坦的欧几里得空间的存在，能导出这些关系式吗？所谓短程线，就是长度最短的线段，如果没有欧几里德几何对长度的定义，如何计算曲线的长度和积分？如果没有欧几里得几何对曲线微分和高阶导数的定义，如何定义并计算曲率？又比如大家都知道的，球面上的三角形的内角之和大于180度。曲面上的角度如何定义呢？定义为两个相交的大圆的切线之间的夹角。而这切线，就是欧几里得空间的直线。如果没有一个均匀平坦的刚性的欧几里得空间作为本底，任何曲面几何都将寸步难行。
从逻辑上讲，所谓弯曲，是相对于平坦而言。如果没有平坦空间，如何定义弯曲空间？时空弯曲论者认为，没有引力的时空才是平坦的。可是我们知道整个宇宙中都存在引力，事实上引力的存在是宇宙学的基本前提之一。那么按照时空弯曲论，宇宙间根本就不存在平坦时空。既然如此，所谓的“弯曲”，就完全失去了现实的比较标准。
五。均匀的时间是一种数学极限
时间相对论者们为时间的相对性辩护的最得意的武器之一就是坚持任何科学上的钟都不能用来作为量度时间的仪器，时间只能用他们设计的“光子反射钟”和“几何动力钟”来量度。“光子反射钟”是达尔文（C.G. Darwin，不是那个进化论的发明者）为了解释钟佯谬于1957提出来的。他认为时间的测量必须通过不同的观测者之间互相发送和接收光线来实现。这种假想的理论钟不仅根本无法实现，而且在理论和逻辑上也站不住脚，因为它导致时钟的快慢与速度的方向有关 – 相互离开的速度使时间延缓，相互靠近的速度使时间加快。这完全违背狭义相对论。尽管如此，许多教科书上仍然大大方方地抄袭达尔文的这一辩解。他的这种“光子反射钟”机制被有些理论家们应用到广义相对论的时间测量。1964年，马兹克（R.F. Marzke）和惠勒（J.A. Wheeler）设计了一种理论的“几何动力钟”（geometrodynamic clock），就采用这种光线发收机制。只是因为在引力场中，不存在任何惯性参照系，因此任何一个参照系都没有一个共同的时间！所以，这种想象的“几何动力钟”不仅有一个不断校对时钟同步的问题，而且还有一个不断校准快慢的问题。引力场中的时间都是定域的（local）而不是全域的（global），这就造成整个“几何动力钟”概念的根本性混乱。这种校准还需要比光速还快的，理论上无穷快的某种信号才得以实现。就连他们自己也知道，这种假想的“几何动力钟”是一个“永远无法实现的理论家的梦想”。
所谓的“光子反射钟”和“几何动力钟”的发明者强加于物理学界的概念是，只有他们的假想钟才能用来测量时间，其他一切实际钟表的测量都不算数。他们要在相对论讨论中完全取消任何实际钟的资格。他们是要用钟表的精度问题来否认这样一个事实：理论上的时间可以被各种不同的自然过程来测量，而且可以被越来越精确的实际钟表逐渐逼近。
因为时间和空间为所有自然过程所共有，它也就可以为不同的自然过程来量度，来互相印证。而这，也就是时间和空间的本质。时间的均匀性和绝对性也只有在这样的互相印证和逐渐逼近中才能体现。时间可以通过天体的运行，动植物的寿命，单摆的周期，电子振荡器或原子振荡的频率，放射性同位素的自然衰变，山石的风化，铁管的氧化程度，美国总统换届的次数，等等等等，来共同测定。这些不同的过程各有优劣，互为短长。比如说，摆钟和电子表方便适用，原子钟准确但不方便，这些钟表不适用于测量漫长的过程如古尸的年代鉴定和地质结构的断代，只有同位素的衰变能测量这种漫长的过程。但是这种“同位素钟”不太准确。既准确又稳定，能够测量这样漫长的过程的钟表是天体的运行。但天体钟没有小刻度，不能用来量度短时间和快过程。人的衰老过程，并不是很精确的过程，可是他在揭示钟佯谬的逻辑矛盾，确立时间的客观本质上却起到了其他钟表无法替代的作用。这些不同的过程的测量精度各不一样，但并不妨碍他们所量度的时间的真实性和公共性。真实性和准确度不是同一个概念。科学上所有的测量都有误差，都不可能绝对精确。如果因为测量误差而否认真实性，那实验科学上的所有测量就没有一个是真实的。
测量误差和真实性如何统一呢？在于无限逼近。无限逼近是微积分和近代数学的基础。不能掌握数学极限的概念的人就无法入微积分的门。也就不能理解曲线的斜率，曲率，短程线，面积和体积的积分，密度，速度，加速度，矢量场的梯度，散度和旋度等概念。这些数学量和物理量的真实存在是不容置疑的，可是却无法绝对精确地测量。实验仪器和电脑的数值计算永远无法精确测量或计算微分，只能得到近似的差分。有些极简单的数学概念，比如点，直线和平面，现实中就无法找到，只能通过数学极限的概念来把握。现实中不存在真正的平面，但这并不能否认数学平面的真实性。人们可以通过平整的木板，墙壁，镜面，页岩和石英的断面，盆里的水面和平静的湖水等等来抽象出一个理论上绝对平坦的数学平面。同样，现实中的直线不是绝对的直。即使莱塞光也会因媒质的不均匀而弯曲。但是人们可以通过桌椅的边，直尺，木工的拉线，步枪的瞄准线，莱塞的光线等等来逼近理论上的直线，也可以想象两个抽象的数学平面的相交线来把握绝对的直线的真实性。物理世界的点都是有尺寸的，而数学上的点是无穷小的。总之，实验测量与理论极限的差别不能成为否认这些数学物理量的真实性的理由。
时间又何尚不是如此。为所有自然过程所共有的均匀的单向时间是我们通过诸多物理，化学，生物，历史等等过程来测量来把握的。因为我们有许多测量时间的方法，这就使得许多逻辑诡辩无可逃遁。这是时间的相对论者要排除所有实际的钟表，而代之以他们的假想的无法实现的钟表的真正原因。质言之，他们就是要用可以逃避实践检验的理论和仪器来取代可以通过实践来检验的理论和科学仪器，因为他们的理论和假想仪器经不起实践和逻辑的检验。
等效原理（equivalence principle）尤其是強等效原理，在廣義相對論的引力理論中居於一個極重要的地位，它的重要性首先是被愛因斯坦分別在1911年的《關於引力對光傳播的影響》及1916年的《廣義相對論的基礎》中被提出來。
等效原理共有兩個不同程度的表述：弱等效原理及強等效原理。
對此原理，愛因斯坦曾如是說：「我為它的存在感到極為驚奇，並且猜想其中必有一把可以更深入了解慣性和引力的鑰匙。」
目录
[隐藏]弱等效原理[编辑]
弱等效原理原是指觀測者不能在局部的區域內分辨出由加速度所產生的慣性力或由物體所產生的引力，而它是由引力質量與慣性質量成正比例這一事實推演出來，這個關係首先是由伽利略及牛頓用一系列的實驗斷定出來。伽利略及牛頓的實驗[编辑]
早在17世紀，伽利略已利用物體從斜面滾下不同的距離所需要的時間，去證明物體於地球上的自由下落的加速度是一個常量；另外，伽利略亦發現單擺的週期只與擺長有關，而與擺錘的質料無關。稍後的牛頓則做了兩個等長而同形狀的單擺，其中一個的擺錘是用金做的；而另一個擺錘用等重的銀、鉛、玻璃、沙等不同物料製成。而牛頓在多次實驗均未能觀察到它們之間的週期差異。從牛頓力學來說，質量本身被付予兩種不同的意義：一個從動力學方程式（牛頓第二定律）引入：
是指慣性質量，代表著物體運動的慣性，即是物體抵抗運動變化的程度；另一方面，從牛頓萬有引力定律：是代表物體引力大小的一個參數，稱作引力質量。至此可從定量分析去理解兩種不同物理量的關係：
從斜面的落體運動分析，可知
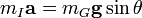
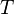則表示為：
的精確度於1680年接受了的結論。在牛頓之後，厄阜於1890年25年間，以鉑為基準用八種不同的材料去進行攏扭實驗，去測量引力質量與慣性質量的比例與1的偏離，從實驗的精確度，厄阜的結論是：
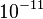；到了1971年，布拉金斯基及潘洛夫等人又將實驗之精確度推至
。此外還有別的科學家用實驗測定了原子和原子核的結合能所對應的引力質量與慣性質量之比，亦沒有發現對1之偏離（雖精確度不及厄阜攏扭實驗）。因此，在目前的精確度甚高之下，可證實：愛因斯坦的思想實驗[编辑]
自牛頓至愛因斯坦的200余年間，人們對引力質量及慣性質量相等的事只是當成偶然的事件，並沒有深刻去研究，直至愛因斯坦完成狹義相對論後，要處理引力理論和相對性原理的調和問題，方始注意。愛因斯坦曾說：引力場中一切物體都具有同一的加速度，這條定律也可表述為慣性質量同引力質量相等，它當時就使我認識到它的全部重要性。我為它的存在感到極為驚奇，並且猜想其中必有一把可以更深入了解慣性和引力的鑰匙。
愛因斯坦用一個思想實驗來說明：在遙遠的宇宙深處（慣性參考系），有一個密封的太空船在
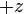方向向上加速，其加速度為
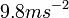，假設密封的太空船內有一個太空人及一個鉛球，該太空人在太空船內拿起一塊鉛球，他感受到鉛球有重量；不單如此，他自己亦感受到自身有重量，他認為這有兩個可能性：一是太空船在太空中正在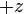方向向上（相對於太空人）加速，雖然附近沒有任何星球或重力場，太空人仍會感覺到因鉛球及自身的慣性關係有下墜的傾向，這就是慣性力。另一個可能性是太空船可能停在一顆行星上，其引力場強度是
，它利用萬有引力來拉扯著鉛球及自己，使他感到鉛球及自己的重量。另一個思想實驗是：在大廈內的升降機不幸地斷了鋼索，升降機正以加速度
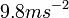向下加速，假設升降機槽無限長，升降機內有乘客及一個鉛球，裡面的乘客可觀察到鉛球及自己會浮在半空，即是“失重”。他認為這有兩個可能性：一是升降機在升降機槽中正在
方向向上（相對於升降機槽）加速，乘客及鉛球正跟著升降機加速。另一個可能性是升降機可能在遙遠的宇宙深處，其引力場強度是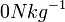
，沒有萬有引力來拉扯著鉛球及自己，使他感受不到鉛球及自己的重量；由於乘客認為沒有任何力施加在自己及鉛球上，所以加速度為
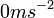，是慣性參考系。現在可從定量的分析去討論上述兩種情況，從第一個思想實驗可知：
（從太空船外）
（從太空船內）及
，所以法向反作用力
相同，密封太空船內的太空人不可能分辨出重力所做成的重量或由慣性做出的“重量”。由第二個思想實驗可知：
（從升降機外）
及 
（從升降機內）及法向反作用力
（任何物體沒有與升降機接觸），升降機內的乘客不可能分辨出加速度所抵消的引力場強度（假慣性參考系）或由真正為零的引力場強度及加速度（真慣性參考系）。由此可見，無論任何動力學方法，只要有
，是不能分辨引力場強度及加速度的動力學效應；甚至或是慣性參考系和非慣性參考系的動力學效應都是不能分辨，其中的兩類觀察者都是能用各自的方式去正碓描述事實，所以這兩種分析方法是等效的，這就是弱等效原理。
No comments:
Post a Comment