孙会元固体物理基础第三章能带论课件3.1布洛赫定理及能带_ ...
wenku.baidu.com/view/0f6d5cb4f61fb7360b4c65ee
轉為繁體網頁
轉為繁體網頁
2014年3月11日 - 孙会元固体物理基础第三章能带论课件3.1布洛赫定理及能带_理学_高等教育_教育 ... Rn 其中Rn 的本征函数是按布拉维格子周期性调幅的平面?
[PPT]所以绝对零度时的费米温度为
无任何限制的自由电子性质：动量具有确定值，速度与波的群速度一致，而坐标不 ... 例如铜:铜是面心立方晶体,晶格常数 . ... 实际上,电子在晶体内运动时,要受阻力作用.
netclass.csu.edu.cn/.../ppt/第四章_金属自由电子理论.ppt
轉為繁體網頁
轉為繁體網頁
孙会元固体物理基础第三章能带论课件3.1布洛赫定理及能带_ ...
孙会元固体物理基础第三章能带论课件3.7 布洛赫 ... - 百度文库
孙会元固体物理基础第三章能带论课件3.8 布洛赫电子在恒定 ...
wenku.baidu.com/view/3c18515910a6f524cdbf8536
轉為繁體網頁
轉為繁體網頁
孙会元固体物理基础第三章能带论课件3.4 能带结构其它计算 ...
max.book118.com › 海量文档 › 临时分类 - 轉為繁體網頁
孙会元教授主编固体物理基础第五章固体输运现象课件5.2 ...
max.book118.com › 海量文档 › 临时分类 - 轉為繁體網頁
孙会元固体物理基础第一章1.1 模型及基态性质.ppt 全文文档 ...
max.book118.com › 海量文档 › 临时分类 - 轉為繁體網頁
孙会元固体物理基础第三章能带论课件3.7 布洛赫 ... - 淘豆网
www.taodocs.com › 研究报告 › 教育
轉為繁體網頁
轉為繁體網頁
phymath999: 傅立叶变换from 空间域to 时间域或频率域; 共轭 ...
phymath999.blogspot.com/2015/03/from-to.html
轉為繁體網頁
轉為繁體網頁
《固体物理》课件PPT 19 能态密度和费米面- 道客巴巴
www.doc88.com/p-178809918791.html
轉為繁體網頁
轉為繁體網頁
第三章金属自由电子理论_固体物理课件- 道客巴巴
www.doc88.com/p-73048445851.html
轉為繁體網頁
轉為繁體網頁
布洛赫波[编辑]
维基百科，自由的百科全书
在固体物理学中，布洛赫波（Bloch wave）是周期性势场（如晶体）中粒子（一般为电子）的波函数，又名布洛赫态（Bloch state）。
布洛赫波因其提出者美籍瑞士裔物理学家菲利克斯·布洛赫而得名。
布洛赫波由一个平面波和一个周期函数
（布洛赫波包）相乘得到。其中 与势场具有相同周期性。布洛赫波的具体形式为：
为晶格周期矢量。可以看出，具有上式性质的波函数可以写成布洛赫函数的形式。
平面波波矢
（又称“布洛赫波矢”，它与约化普朗克常数的乘积即为粒子的晶体动量）表征不同原胞间电子波函数的位相变化，其大小只在一个倒易点阵矢量之内才与波函数满足一一对应关系，所以通常只考虑第一布里渊区内的波矢。对一个给定的波矢和势场分布，电子运动的薛定谔方程具有一系列解，称为电子的能带，常用波函数的下标n 以区别。这些能带的能量在 的各个单值区分界处存在有限大小的空隙，称为能隙。在第一布里渊区中所有能量本征态的集合构成了电子的能带结构。在单电子近似的框架内，周期性势场中电子运动的宏观性质都可以根据能带结构及相应的波函数计算出。
上述结果的一个推论为：在确定的完整晶体结构中，布洛赫波矢 是一个守恒量（以倒易点阵矢量为模），即电子波的群速度为守恒量。换言之，在完整晶体中，电子运动可以不被格点散射地传播（所以该模型又称为近自由电子近似），晶态导体的电阻仅仅来自那些破坏了势场周期性的晶体缺陷以及电子与声子的相互作用。
从薛定谔方程出发可以证明，哈密顿算符与平移算符的作用次序满足交换律，所以周期势场中粒子的本征波函数总是可以写成布洛赫函数的形式。更广义地说，本征函数满足的算符作用对称关系是群论中表示理论的一个特例。
布洛赫波的概念由菲利克斯·布洛赫在1928年研究晶态固体的导电性时首次提出的，但其数学基础在历史上却曾由乔治·威廉·希尔（1877年），加斯东·弗洛凯（Gaston Floquet，1883年）和亚历山大·李雅普诺夫（1892年）等独立地提出。因此，类似性质的概念在各个领域有着不同的名称：常微分方程理论中称为弗洛凯理论（也有人称“李雅普诺夫-弗洛凯定理”）；一维周期性波动方程则有时被称为希尔方程（Hill's equation）。
布里渊区[编辑]
布洛赫波因其提出者美籍瑞士裔物理学家菲利克斯·布洛赫而得名。
布洛赫波由一个平面波和一个周期函数
（布洛赫波包）相乘得到。其中 与势场具有相同周期性。布洛赫波的具体形式为：
为晶格周期矢量。可以看出，具有上式性质的波函数可以写成布洛赫函数的形式。平面波波矢
（又称“布洛赫波矢”，它与约化普朗克常数的乘积即为粒子的晶体动量）表征不同原胞间电子波函数的位相变化，其大小只在一个倒易点阵矢量之内才与波函数满足一一对应关系，所以通常只考虑第一布里渊区内的波矢。对一个给定的波矢和势场分布，电子运动的薛定谔方程具有一系列解，称为电子的能带，常用波函数的下标n 以区别。这些能带的能量在 的各个单值区分界处存在有限大小的空隙，称为能隙。在第一布里渊区中所有能量本征态的集合构成了电子的能带结构。在单电子近似的框架内，周期性势场中电子运动的宏观性质都可以根据能带结构及相应的波函数计算出。上述结果的一个推论为：在确定的完整晶体结构中，布洛赫波矢
是一个守恒量（以倒易点阵矢量为模），即电子波的群速度为守恒量。换言之，在完整晶体中，电子运动可以不被格点散射地传播（所以该模型又称为近自由电子近似），晶态导体的电阻仅仅来自那些破坏了势场周期性的晶体缺陷以及电子与声子的相互作用。从薛定谔方程出发可以证明，哈密顿算符与平移算符的作用次序满足交换律，所以周期势场中粒子的本征波函数总是可以写成布洛赫函数的形式。更广义地说，本征函数满足的算符作用对称关系是群论中表示理论的一个特例。
布洛赫波的概念由菲利克斯·布洛赫在1928年研究晶态固体的导电性时首次提出的，但其数学基础在历史上却曾由乔治·威廉·希尔（1877年），加斯东·弗洛凯（Gaston Floquet，1883年）和亚历山大·李雅普诺夫（1892年）等独立地提出。因此，类似性质的概念在各个领域有着不同的名称：常微分方程理论中称为弗洛凯理论（也有人称“李雅普诺夫-弗洛凯定理”）；一维周期性波动方程则有时被称为希尔方程（Hill's equation）。
布里渊区[编辑]
维基百科，自由的百科全书
在数学和固体物理学中，第一布里渊区（Brillouin zone）是动量空间中晶体倒易点阵的原胞。第一布里渊区在几何上与布拉菲点阵中的维格纳-赛兹原胞类似。布里渊区的重要性在于：周期性介质中的所有布洛赫波能在此空间中完全确定。
在点阵空间中，作某一个阵点与其所有相邻阵点的垂直平分面，这些平面包围的空间就是包含前述阵点的第一布里渊区；亦可等价地定义为：在k空间（即波矢空间或倒易空间）中，从原点出发，不穿越任何布拉格衍射面所能到达的点的集合，就是第一布里渊区。
在上述定义中，若作的是某阵点和它所有次近邻阵点的垂直平分面，则得到的是第二布里渊区；若作的是某阵点和它次次近邻阵点的垂直平分面，则得到的是第三布里渊区，依此类推。但高阶布里渊区用得很少，因此“布里渊区”常常仅指“第一布里渊区”。
本概念最早由法国物理学家莱昂·布里渊（Léon Brillouin）提出。
在点阵空间中，作某一个阵点与其所有相邻阵点的垂直平分面，这些平面包围的空间就是包含前述阵点的第一布里渊区；亦可等价地定义为：在k空间（即波矢空间或倒易空间）中，从原点出发，不穿越任何布拉格衍射面所能到达的点的集合，就是第一布里渊区。
在上述定义中，若作的是某阵点和它所有次近邻阵点的垂直平分面，则得到的是第二布里渊区；若作的是某阵点和它次次近邻阵点的垂直平分面，则得到的是第三布里渊区，依此类推。但高阶布里渊区用得很少，因此“布里渊区”常常仅指“第一布里渊区”。
本概念最早由法国物理学家莱昂·布里渊（Léon Brillouin）提出。
http://210.45.128.5/jpkc/jpkcwlxgt/lesson/ch05/0505.htm
§单电子近似与布洛赫波(Bloch wave)
（本节重点：什么是布洛赫波？它有什么性质？）
用量子力学来解决多体问题是非常复杂的, 而且严格解是不可能的。要解决这些问题, 只能抓住主要矛盾, 建立模型, 作充分的近似, 才可以求解。 其中把多体问题简化为单电子问题, 需要经过多次简化:
第一步是把原子核与核外内层电子考虑成一个整体——离子实，使原子中的多体问题简化为离子实与外层电子的问题；第二步是绝热近似，考虑到离子实的质量比较大，离子运动速度相对慢，位移相对小，在讨论电子问题时，可以认为离子是固定在瞬时的位置上, 这样, 多种粒子的问题就简化成多电子问题; 第三步，忽略电子之间的相互作用（理想电子气），利用哈特里－福克自洽场方法, 多电子问题简化为单电子问题, 每个电子是在固定的离子势场和其他电子的平均场中运动; 第三步的简化是认为所有离子势场和其他电子的平均场是周期性势场。
  
其中:
 ； ， 是用来表征电子状态的量子数。
如果,
 ,   ，
这就回到索未菲模型。
对实际晶体,
 是个周期势场, 布洛赫证明: 图5.2-1 (5.2.3)  (5.2.4)
或
 (5.2.5)
布洛赫定理的证明详见(课本P154-157)。
 称为布洛赫波（Bloch 波）。
〖
设普通解为:
 , 其中 为特解.  ； 为布洛赫定理。〗
讨论:
1. 电子不再是属于局域的特定原子, 而是扩展于整个晶体,
为电子的晶体轨道。因子 反映了电子公有化运动, 如果令 , 则 为相邻原子波函数的位相差, 反映公有化运动状态。这表现在: a) 布洛赫波在严格的周期场下是可以传播的, 且波(电子)的空间分布也是周期性的; b) 在实空间电子态(波)的重迭程度, 重迭程度越大, 公有化运动状态越强。
2. 电子的波函数
是一个被周期函数所调制的平面波或被平面波调制的周期函数。
3. 布洛赫波函数中的
 是波矢量, 可用它来标记电子的状态, 电子波矢只需取一个布里渊区范围, （理由下面讨论，即波函数的平移对称性。）
对
  
可见, 波矢差为倒格矢的波函数都对应相同的本征值. 为了使
与平移算符本征值一一对应, 我们把限制在第一布里渊区。（这里只讨论了实空间的平移对称操作, 对k空间的平移对称操作后面再作讨论。）
而且, 电子波函数
并非动量算符的本征态,  也不是其本征值, 可从下式右边第二项一般不为零来说明:
所以
 不是布洛赫电子的真实动量。在研究晶体在外场作用下运动及电子与声子, 光子的相互作用时, 它在形式上又好象起到动量的作用, 所以又称为布洛赫电子的赝动量或电子的晶体动量。它是作为共有化运动的‘动量’。
4. 应使用周期性边界条件, 则
受到限制: (5.2.6)
从(5.2.5)式得:
 (5.2.7) (5.2.8) (5.2.9)只能取分立值，其最小间隔为 ；在第一布里渊区内所能取的分立状态（或分立点的数目）为(2p/a)/(2p/Nia)=Ni。于是我们估算波包在实空间的扩展程度: 由测不准关系:  ； ； ，分辨kx要求 ， ，即电子在实空间位置的不确定程度, 或反映电子的公有化运动程度。这就回到了讨论1.
可应用量子力学的微扰论, 对晶体的特性作推算。
5.【对接近布里渊区边界的情况, （为简单起见, 对一维情况采用方法3.）
 (5.3.31)  (5.3.32)
波函数为:
把它代入薛定谔方程,
两边分别乘以
 和 然后对x积分, 类似地有: 
要使A及B有非零解, 其系数行列式必须为零, 从而有:
 (5.3.35)
或
 (5.3.36) 
其中,
 代表自由电子在k =  状态的动能。
当D=0,
 ；代入(5.3.33)和(5.3.34)式, 解得 , 故其零级近似波函数与(5.3.29)和(5.3.30)式一致。
对D¹0, 同时假设 TnD << |Vn| < Tn, 即偏离得很小，把(5.3.36)式用项式定理展开,保留到D2项, 得：（用到:
 ；并令 ） (5.3.37)  (5.3.38)
这说明在禁带之上的一个能带底部, 能量E+ 随相对波矢D的变化关系是向上弯的抛物线. 在禁带下边能带顶部, 能量E- 随相对波矢D的变化关系是向下弯的抛物线.
不难证明, 如果
 比 |Vn| 大得多, 2TnD >> |Vn|, 即偏离很大或公有化运动特性强, 由(5.3.36)式可得：（用到:；并令 ） ; (5.3.39)  (5.3.40)
这个结果同非简并微扰结果相近, 在其他所有波矢状态中保留一个k’, 它对状态k有特别大的影响。】
|
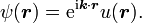
No comments:
Post a Comment