Tuesday, April 21, 2015

高斯 Gauss 黎蔓曲率实际上分为2部分，一部分是里奇的，由物质分布在代数上决定，另外一部分，则是外尔张量，属于引力本身的自由度 ; riemann ds2=g11du2+g12dudv+g21dvdu+g22dv2, 其中g11，g12，g21，g22均为变量u和v的函数，称之为度规，它们由曲面的物质所决定

 

果

    史瓦西时空的外尔张量

    我们知道，真空，也会弯曲。
    这是爱因斯坦引力场方程的真空解。
    那么，黎蔓曲率实际上分为2部分，一部分是里奇的，由物质分布在代数上决定，另外一部分，则是外尔张量，属于引力本身的自由度。
    这外尔张量，今天我叫我的徒弟去计算了。还看不出结果，估计要用maple。

    最近中国事情太多，让人非常失望，我在教育网的blog也被封杀，只要跑到网易，开了一个微博：虽然我不太有时间写，也就是所谓真空，但希望引起时空弯曲：

    黎曼曲率有多少个独立分量？


    最近，我培养了一个高中刚毕业的徒弟来跟我学习相对论。教了几次以后，我叫他去算球面上的克里氏多夫符号，他很快就算出来了。
    于是，我叫他去算一下n维弯曲空间，黎曼曲率有多少个独立分量？结果他通过排列组合的方法，也得到了一个自己的公式。
    而且居然是对的。

    有兴趣的人可以去算一下，在6维中，有105个独立分量哦

  1. [PDF]望远镜和天文学：400 年的回顾与展望 - 中国科学院国家 ...

    www.niaot.cas.cn/kxcb/.../P020090910367702737153.pdf

    轉為繁體網頁
    关键词天文学，望远镜，国际天文年，天文学史，中国天文学，天文学的成就，暗物质，暗能量. Telescopes and ...... 的，最早是根据爱因斯坦场方程的史瓦西解成功地解. 释了水星 .... 1998 年）表明，宇宙膨胀是加速的，因之，真空能还必. 需产生一个负的 ...


 
《当代物理学进展》二十

 
（三）现代引力理论进展
1.  爱因斯坦前引力理论的回顾
　　从牛顿时代至今，人类对引力的定量研究已有三百余年，在这三百年中，引力研究经历了复杂而曲折的过程。牛顿在1686年所建立的引力定律，涉及的仅只是两质点间的作用力。意大利-法国天文学家和数学家拉格朗日(La-grange,JosephLouisComtede1736～1813)曾致力研究牛顿“留下的一个悬而未解的问题”，这就是找到解决两个以上天体系统运动的数学方法。他与其学生法国天文学家、数学家拉普拉斯(Laplace,PierreSimonMarquisde1749～1827)合作，研究了太阳系的天体摄动问题。1773年，拉格朗日引入引力场概念，并建立了引力势函数。 1782年，拉普拉斯建立了自由空间的引力势函数的微分方程，即拉普拉斯方程2V=0，并于1799～1825年间，撰写成功五大卷《天体力学》巨著。在这部著名的传世之作中，拉普拉斯对经典引力理论做了系统的总结。以后，拉格朗日及拉普拉斯的学生泊松(Poisson,SimeonDenis1781～1840)又继续了他的两位老师的引力研究，于1813年推广了引力场理论，建立了引力场的泊松方程2V=4πGρ。引入了引力场概念后，引力理论从牛顿引力形式下得到了推广。尽管，引力理论已发展到相当完善的程度，但是它仍存在有几个较为明显的问题。首先，由于不显含时间，这一引力理论仅能描述超距作用，其二，它不具有洛仑兹变换下的协变形式。普适性是物理理论的生命，而协变性就是普适性的重要特征，一个具体的物理规律如果不能纳入协变性的理论框架，它的普适性就值得怀疑。此外，在引力领域内，人们还发现了牛顿理论所不能解释的水星近日点的进动问题，首先发现这一问题的是海王星的发现者、法国天文学家勒威耶(Leverrier，UrbainJeanJoseph1811～1877)。海王星的发现曾使牛顿引力理论的威信达到了它的顶峰。勒威耶先通过计算预言，以后经观测证实了海王星的存在。在牛顿理论发展的全部历史过程中，通过纯粹的计算发现一颗巨大的行星成为当时人们瞩目的一项伟大成就，可以说，它消除了人们对牛顿理论价值的最后一点疑虑。然而，富有戏剧性的是，正是这位对牛顿理论正确性做出重大贡献的勒威耶，却在发现海王星的头一年，即1945年，通过计算发现了水星的反常运动，水星的近日点进动值比牛顿理论的预期值每百年快35″。这一发现被加拿大天文学家纽科姆(Newcomb，Simon1835～1909)观测证实，他得到的这一进动附加值是43″/百年。虽然牛顿引力出现的这一微小偏差，远不足以使当时的人们产生紧迫感，然而“能在如此完美无瑕的牛顿理论中，发现某种瑕疵，这本身就是一项非常了不起的成就”①，因为它们有可能成为新引力理论的生长点。
　　1906年，法国数学家庞加莱(Poincare，JulesHenri1854～1912)在所发表的一篇论文中，以实现洛仑兹群协变的要求为前提，构造了第一个相对论引力理论②。他认为洛仑兹变换下的协变性不仅应体现在麦克斯韦电磁场方程的数学结构中，对于一切非电磁起源的力，包括引力，也应具有类似的协变特征。与此同时，庞加莱还指出，引力作用也像电磁作用一样具有光速的传播速度。以后，俄国-德国数学家闵可夫斯基(Minkowski，Hermann 1864～1909)和德国物理学家索末菲(Sommerfeld，Arnold Johannes Wilhelm 1868～1951)又把这一理论表述为四维矢量分析形式。尽管庞加莱、闵可夫斯基等人的引力协变理论尚存在着一些缺陷，但是他们毕竟找到了第一个协变性的引力理论，由这一理论得出的计算结果与观测值相比较，比牛顿理论的精确度要高，它还成功地给出了引力质量与惯性质量的等同性解释，更注意满足了场论的要求。他们的工作，不仅为以后的物理理论几何化研究奠定了基础，而且这一理论的尝试与缺陷都已成为爱因斯坦建立更为成功的引力理论的借鉴。
2.  爱因斯坦建立新引力理论的最初尝试
　　虽然洛仑兹与庞加莱对洛仑兹变换都有着农厚的兴趣，但是真正能够理解它，并赋予它物理实在意义的却是爱因斯坦。在这方面，他们之间的主要差异就在于对时间，即同时性的理解。只有认识到，时间与空时不可分割，它们统一在同一个变换方式之中，才能真正地把洛仑兹变换当成一种物理实在，而不仅仅是一种数学手段。
　　1905年，爱因斯坦发表了《论动体的电动力学》论文①，“爱因斯坦用他的相对论发动了物理科学中的一次思想革命”②，在这篇论文中，爱因斯坦是这样总结的，“狭义相对论导致了空间和时间物理概念的清楚解释，并且由此认识到运动着的量杆和时钟的行为。它在原则上取消了绝对同时性概念，从而也取消了牛顿所理解的那个即时超距作用概念。它指出在处理同光速相比不是小到可忽略的运动时，运动定律必须加以修改。它导致了麦克斯韦电磁方程形式上的澄清，特别是导致了对电场和磁场本质上同一性的解释。它把动量守恒和能量守恒这两条定律统一成一条定律，并且指出了质量与能量的等效性。”① 1907年，爱因斯坦又在《关于相对论原理和由此得出的结论》论文中②，进一步阐明E=mc2的意义。1906年，相对论的最早支持者普朗克证明③，运动方程可以借助引入拉格朗日函数L=-m0c2（1-v2/c2）1/2利用最小作用量原理推出。1907年，担任普朗克助教的德国物理学家劳厄(Laue, Max The odor Felixvon1879～1960)运用相对论运动学导出了菲涅耳曳引系数，并解释了菲索实验。1909年美国物理学家刘易斯(Lewis, G.N.)和托尔曼对具有绝对时空观的牛顿力学进行了改造，引入了相对论动量，使动量守恒与能量守恒定律具有了协变形式，为相对论动力学研究奠定了坚实的基础。在这些成果中，最引人瞩目的、也是对广义相对论的建立最具有影响的是闵可夫斯基四维时空的提出。1908年9月21日在科隆举行的第八届德国自然科学家和医生大会上，闵可夫斯基做了《空间和时间》的著名讲演。闵可夫斯基不仅是爱因斯坦以外，第一个明确了时空观念的变化，同时还利用他的四维时空给予了相对论理论一个非常优美和简洁的数学形式。他的四维理论在简化了相对论理论体系的同时，也成为狭义相对论向广义相对论过渡的连接纽带，自然为广义相对论的建成奠定了基础。
　　狭义相对论的两个缺陷是明显的，①它依赖于惯性系，并承认它的特殊地位。②在它的理论框架中，不包容引力理论。最初，爱因斯坦试图在狭义相对论的理论框架之中，建立一个新的相对论理论，以包容引力理论。“最简单的作法是当然保留拉普拉斯的引力标量势，并用一个关于时间微分项，以明显的方式来补足泊松方程，使狭义相对论得到满足。”①但是，很快地他就察觉到了其中的困难，而且意识到“虽然惯性和能量之间的关系已经如此美妙地从狭义相对论中推导了出来，但是惯性和引力之间的关系却没能得以说明，我猜想，这个关系是不能依靠狭义相对论来说明的。”
3.  物理几何化
　　在建立相对性引力理论过程中，爱因斯坦、庞加莱及闵科夫斯基最初的尝试都未能成功，其关键都在于与理论相关的时空结构。
　　在迈向成功的道路上，爱因斯坦获得飞跃性的认识来源于对刚体转动圆盘的研究。在他1912年2月所发表的《光速和引力场的静力学》一文中，他认为，由于洛仑兹收缩，圆周与半径之比不再为π，这表明，惯性系的观察者得出沿圆周运动方向运动的尺有尺缩效应，而相对非惯性旋转系的观察者根据等效原理，会认为所在系是静止不动的，却存在着一个“离心的引力场”，由于圆周与半径之比不再为π，他自然会解释为，由于这一引力的存在，使欧几里德几何不再成立。将这一结论扩展到一切真实引力场，有引力的空间都将不再是欧几里德的。这就是爱因斯坦所解释的，“把等效原理和狭义相对论结合起来，很自然地得出，引力与非欧几何联系在一起”的结论。当时爱因斯坦对非欧几何所知甚少，仅在大学读书时从基塞(Geiser)教授那里学到一点微分几何的知识，正是其中有关高斯曲面理论使爱因斯坦受到启发。他曾回忆道，“直到1912年，当我偶然想到高斯的曲面理论可能就是解开这个奥秘的关键时，这个问题才获得了解释。我发现，高斯曲面坐标对于理解这个问题是十分有意义的。”①
　　德国数学家高斯(Gauss, Johann Karl Freidrich1777～1855）从大地测量中受到启发，创立了二维曲面的微分几何理论。他在曲面上引入曲线坐标u和v，并证明曲面上任意线元具有如下普遍形式
　　ds2=g11du2+g12dudv+g21dvdu+g22dv2
　　其中g11，g12，g21，g22均为变量u和v的函数，称之为度规，它们由曲面的物质所决定。根据高斯的曲线坐标和度规，不仅可以确定曲面上的测地线（即弯曲空间的“直线”），还可以找到曲面的曲率，并进一步证明曲面所在空间的非欧几里德性质。高斯曲面即为一种弯曲的二维空间结构，然而在其中一点的任意一个小的邻域上，它应近似为平面，在这个局域，欧氏几何仍将成立，并与局域的笛卡尔系相对应。
　　爱因斯坦把引力空间与高斯曲面理论做了类比思考，他发现，引力所在的空间具有类似高斯曲面的几何性质，特别是当他把闵可夫斯基对狭义相对论所做的解释与引力问题联系起来以后，就更认识到其中的重要含意，这些观念成为了广义相对论理论形成的重要因素。他曾说“没有这个观念，广义相对论恐怕无法成长”，因为闵可夫斯基的四维世界“与高斯曲面理论相结合，向人们展示，存在引力场时，空间是弯曲的，欧氏几何不再成立，这表面引力场中不存在全局性的或大范围的惯性系，但对每一时空点附近的一个小的局域而言，却是闵可夫斯基平直的，欧氏几何仍成立，同时也存在与之对应的‘局域惯性系’。”这实际就是“爱因斯坦升降机”的思想。爱因斯坦明确地指出，“高斯的曲面理论与广义相对论间最重要的接触点就在于度规的性质，这些性质是建立两种理论概念的重要基础。”在1912年3月，爱因斯坦在《静引力场理论》中又指出，“等效原理只能在局域中成立”，这一系列思想表明，爱因斯坦看到了引力与时空几何结构间的联系，这就是引力场影响着时空结构，乃至决定着它的度规的规律。
　　在广义相对论建立过程中，更具有重要意义的事情就是爱因斯坦与他的老同学格罗斯曼（Crossmann, M. 1878─1936）的合作。在格罗斯曼的帮助下，他学习了黎曼几何、里奇与列维─契维塔的张量分析，这一理论体系是以高斯-黎曼及克利斯托菲尔关于非欧几何流形的研究为基础发展起来的，它很快地被用到了广义相对论的引力理论之中。从1912年8月开始，爱因斯坦与格罗斯曼合作，先后发表了三篇论文，它们标志着广义相对论走向建成的重要阶段。
　　在1913年，爱因斯坦与格罗斯曼联合发表的重要论文《广义相对论纳要和引力理论》中①，他们提出了引力的度规场理论，用来描述引力场的不再是标量势，而是以10个引力势函数的度规张量，引力与度规的结合，使黎曼几何获得了实在的物理意义，物理研究向着几何化迈进了决定性的一步。
4.  引力场方程的提出
　　在格罗斯曼的帮助下，爱因斯坦找到了适用于广义相对论理论所需要的数学工具──绝对微分学。但是，在一开始所得到的引力场方程只对线性变换才是协变的，还不具有广义相对性原理所要求的，在任意坐标变换下所具有的协变性，这是因为在当时，爱因斯坦还不太熟悉张量运算，他只保留了守恒定律而放弃了广义协变关系。尽管这一尝试还不算成功，以研究复变函数、特殊函数，并于1902年得到拉普拉斯方程普遍解而成名于世的英国数学家惠特泰克（Whittacker, Edmund Taylor1873-1956)却给予它很高的评价。他认为用十个引力势函数g??确定引力场是一个巨大的创新，因为它意味着抛弃一个由来以久的信条，即引力场能被一个单一的标量势所描述①。在爱因斯坦重新回到普遍协变要求，并对黎曼-克里斯托菲尔曲率张量有了新的认识以后，相对论引力理论的研究有了真正的进展。此时，引力问题与两个里奇张量联系在一起，
　　Gim=Rim+Sim
　　　
　　再补充以协变性要求，爱因斯坦得到了引力场方程
　　在自由空间中，该方程变为
　　其中R??是里奇曲率张量，R为标量曲率，T??为能动张量，∧为宇宙学常数。
　　广义相对论理论依赖于两个彼此独立的假定。第一个假定是，引力场对物质的影响可以利用弯曲时空度规g??代替平直时空度规——闵可夫斯基度规描述。其实，这就是等效原理的数学表述，这一假定已被厄阜扭秤实验，以及以后的迪克、贝林斯基(Belinsky)等人的实验所证实。第二个假定便包含在爱因斯坦的引力场方程之中。这个方程假定了描述时空弯曲的度规与物质及能量分布间的联系，又因为能动张量还与其它非引力性质的力有关，这一方程又反映了引力场与其它力的关系。
　　与麦克斯韦电磁场方程不同，引力场方程所包含的十个关于g??变量的方程组都是非线性的，但是，它对任意曲线坐标变换却是不变的。由于缺乏严格解的普遍方法，只能逐个找到特殊情况下的近似解。例如史瓦西所得到的方程解就是静态球对称引力场方程的特殊解，它已经被著名的三大实验所验证。在得到史瓦西解的同时，一个棘手的问题也随之出现，这就是在史瓦西半径上的度规分量奇点的出现。尽管后来爱丁顿与奥本海默分别找到了消除奇点的坐标系，但是直到40多年以后，即1959年，弗伦斯克尔(Fronskel)、芬克尔斯坦(Finkelstein)及克鲁斯克尔(Kruskal)引入了新坐标系，奇点不仅被消除，在r=2M处还能以“咽喉”将两个渐近平直区域连通起来，此时，人们对奇点有了更进一步的认识。
5.  引力波研究
　　在引力几何化的过程中，爱因斯坦很重视引力场与电磁场的相似性。1912年7月，在他写给埃伦菲斯特的一封信中说，他注意到他关于静引力场的讨论对应着电磁理论中的静电场情况，而他所称的“广义静止情况”却与静磁场相似。他的“转动圆盘”将产生一种静止的引力的“磁场”，既然电磁波是一种由电场与磁场相互作用的运动形态，引力的“电”与“磁”分量就有可能对应着引力波的存在。
　　早在1916年，即建立了广义协变的引力场方程不久，爱因斯坦就得到了引力场方程的线性近似引力波波动方程解①。1922年，爱丁顿强调指出，这些解从理论上预言了引力波的存在①。对于物理理论工作者来说，问题在于如何从实验上探测到引力波以证实它的存在，并如何从实验上确定它的性质，如传播速度与偏振特性等。1918年，爱因斯坦首先证明②，仅仅处于加速状态的质量体系，并不能像电磁偶极子辐射电磁波那样，辐射引力波，这是因为质量总是正的，并且一切物体的引力质量与惯性质量总是精确地保持一致的结果。然而，如果一根质量为M、长度为2l的质密棒，沿垂直于棒的中心轴高速旋转，并且具有时变的四极矩时，将会有引力辐射产生。首先设法在实验室条件下，对引力波进行探测的是韦伯③。1970年，他宣布实验探到发自银心的引力波④，虽然这一结果被其后类似的其它实验观测否定，但是韦伯的开拓性工作仍具有很重要的意义。从60到70年代，天文学以及天体物理学的进展表明，某些天体有可能辐射强大功率的引力波。1974年，通过阿雷西波天文台直径305米的巨型射电天文望远镜，泰勒(Taylor，JosephHooten Jr.)和他的研究生赫尔斯(HulseRussellAlen)共同发现了第一颗脉冲双星PSR1913+16⑤。这颗脉冲双星似乎是专门为验证广义相对论而提供的太空实验室。首先，引人注目的是这颗星发出的脉冲频率。它的频率为16.940539184253(1)Hz，只有最后带括号的一位数字才是不准确的。它的频率随时间的变化又极为缓慢，变化率稳定在-2.47583(1)×10-15Hz/s。如果把它视为一台时钟，其精确程度可以与石英钟相媲美。描述脉冲星的轨道运动有五个主要参量，其中一个参量是描述主轴的取向，它类似于太阳系行星的近日点，称为近星点。与水星做对比，它的近星点进动率要比水星近日点进动率高3万倍以上，这就为高精度地验证广义相对论提供了方便。泰勒测量到的脉冲星近星点进动率为4.2262（1）°/年，与广义相对论符合得极好。他们还根据年进动率、轨道延迟时间和引力红移等数据综合分析，得出这颗脉冲星的质量为1.4410（5）M⊙，其伴星则为1.3874（5）M⊙。
　　在此之前，对广义相对论的验证都是在太阳系内获得的，由于太阳的引力很弱，使以前对引力理论的验证（如水星近日点进动、光线的引力弯曲以及信号延迟等）仅限于验证引力理论在弱引力近似情况下与牛顿引力的微小偏移，因而难以提高对引力理论的判断与限制，更不能在弱引力情况下，对引力波的预言做出检验。根据广义相对论，双星系统是一种旋转着的质量四极子，它应能以引力波方式辐射能量。与所有束缚在一起的二体引力系统一样，其运行轨道周期将随着能量的辐射而减小。在发现脉冲双星PSR1913+16以后，泰勒及其后来的合作者威斯伯(Weisberg,J.M.)、曼彻斯特(Manchester,R.N.)等人坚持长时间的跟踪观测，对脉冲星扫过的总轨道角及它们随时间如何偏离的线性关系积累了大量的观测数据。此外，为尽可能准确地判断脉冲周期，还需扣除星际介质色散和地球自身运动的影响，再将脉冲到达时间转换到脉冲星参考系。在这一转换中，除要考虑脉冲星及其伴星相互绕行的轨道运动外，还应考虑脉冲星自转及各种相对论效应。排除了上述各因素的干扰之后，他们得到的该双星系统轨道周期随时间的变化率是
　
　　与按广义相对论理论预计值dpb/dt=-（2.4025±0.0001）×10-12极为接近①②。脉冲双星的发现以及通过对其周期长时间的观测结果，不仅使爱因斯坦的引力理论再一次地获得了高精度地检验，而且进一步证实了引力波的存在，这一重大成果提供了一个基础理论研究与现代高科、技术结合以及各基础研究领域彼此相互渗透的典范。
　　泰勒1941年生于美国费城，1963年毕业于宾夕法尼亚州哈弗福德学院，1968年在哈佛大学天文学系获得博士学位。1968～1969年，在哈佛大学天文台任天文学讲师并从事研究工作。1969～1976年，在马萨诸塞大学任天文学副教授，1976～1981任教授，1981年以后在普林斯顿大学担任物理学教授。研究领域是射电天文学、设计和发展射电天文望远镜与信息处理系统，对脉冲星研究造诣尤深。赫尔斯1972年毕业于马萨诸塞大学，1975年在泰勒指导下，获得博士学位，此间这对师生所研究的课题使他们获得1993年诺贝尔物理学奖。1975～1977年，赫尔斯在美国射电天文台从事研究工作，1977年转入普林斯顿大学，在该校等离子体物理实验室进行研究工作，主要的研究领域是，托卡马克受控热核聚变等离子体中的粒子迁移及原子过程的计算机模拟研究。
　　虽然赫尔斯较早地离开了脉冲星及射电天文研究，泰勒及他以后的合作者们却对脉冲星进行连续观测长达18年之久。他们为引力辐射研究积累了大量的技术数据。已记录的脉冲星PSR1913+16的站心时间就有4500个，其轨道周期的衰减速率的测量精度达到了0.35%，这些数据可以决定五个开普勒轨道参量和一个后开普勒参量，其精度达到了百万分之几，可以从几个不同的方面“对广义相对论作出有说服力的验证，特别检验了‘电四极矩’导致引力辐射，引力波必须以光速传播”①②。为了观测脉冲星周期这样一个随时间二次方偏离的效应，长时间的连续观测是必不可少的。在现今社会中，有一种只看重短期效益、崇尚所谓短线科研的趋向。泰勒和他的几个学生、博士后及其它合作者们，潜心专注于大科技领域中的小课题研究，在阿雷西波研究所使用最普通的仪器设备，耐心地进行令人感到乏味的观测研究长达近20年之久的上千次观测，这种精神境界以及所取得的辉煌成果都为世人提供了出色的范例。近几十年的研究发现，宇宙间大致有三种类型的引力波，除了发自脉冲双星的这种频率稳定而持续的引力辐射外，还有引力波背景辐射，它们是宇宙发展各阶段，特别是早期宇宙各个物理过程残留引力辐射的叠加波，它们与其它背景“噪音”混杂，难以区分与观测；第三种是脉冲式或扰动式的引力波，它们由超新星爆发、致密天体塌缩、活动星系核中的剧烈扰动、星震等形成。这种引力辐射的强度虽然较大，但持续时间极短，频带也比较宽，给观测带来较大困难。比较起来，双星的引力辐射既稳定又能持续，频率还确定。如果两颗子星的质量足够大，相距又比较近，它们互相绕行的速度与加速度都比较大，由于引力辐射损失能量，轨道缩小、周期随之变短的效果就比较明显，观测其轨道周期的变化率，将不仅能定量地检测引力波的存在，还能确定引力辐射的特征。到本世纪90年代初为止，在证实引力辐射方面，除了人们公认的PSR1913+16是满足上述条件的最好观测目标以外，1990年还发现了脉冲双星 PSR1534+12，它的轨道周期为36351.70270秒，两颗子星相距很近，质量均为1.3M⊙。目前正在积累观测资料，以准确地确定其轨道周期变率，人们正期待着这一观测前景。
6.  引力理论的进展
　　引力是自然界最弱的相互作用，过去在相当长一段时间内，引力研究的进展不仅缓慢，而且除了天体物理以外，与其它学科的联系也甚少。然而，近二三十年来，情况却有所改观，一方面是引力物理随着宇宙学与高能天体物理的进展而发展，另一方面，在凝聚态物理、材料科学中，微引力物理的发展令人瞩目地崛起，与此同时，引力理论自身也在迅速地发展着。最初，引力理论沿着两个不同的方向发展，一是把电磁场理论纳入引力理论之中的研究，一是引力理论向宇宙学方向发展。(1)引力与电磁场的统一性研究
　　电磁场是一种规范场，麦克斯韦方程是一种最简单的规范场方程。包括电磁场、引力场在内的规范场都可以被视为一种几何结构，它们都具有拓扑性质，也具有可以以几何方式表述的辐射特征。在建立相对论后不久，爱因斯坦即注意到了这些相似性。他认为“存在两个独立的空间结构，引力的、电磁的，这两种场应该存在于一个统一的空间结构之中。”1930年以后，爱因斯坦把他的大部分精力投入到引力与电磁力的统一研究之中。与爱因斯坦一起，还有几位数学家，如列维-契维塔(Levicivi-ta)、嘉当(Cartan)、魏尔(Weyl)等人，都热衷于这一工作。魏尔曾试图像爱因斯坦那样，从几何学上用弯曲时空解释这两种力。他确信，通过对时间、空间连续体的研究，可以把引力与电磁力联系起来。首先必须把电磁场方程用于黎曼空间，以便与爱因斯坦的引力理论接轨。为此，魏尔大胆地尝试着应用规范不变性的设想①，令时空两个无限临近点x?与x?+dx?间，
考虑到在规范变换中，各时空点的变换率不同，而且为保持变换不变性要求，相同的方式出现，按此方式可以把电磁学统一起来。虽然在初期，这一工作取得了一些进展，但是毕竟引力场与电磁场分属于两个完全不同的范畴，进一步的研究遇到了难以克服的困难。泡利和爱因斯坦都认为魏尔的理论虽然在数学上很有趣，但与电磁学理论的联系越来越远，以致后期的进展不大，最后魏尔放弃了原来的想法。
　　在量子力学诞生后，于1927年，福克(Fock)和伦敦(London)注意到电磁动量应用
　　i的引入表明，应当把规范变换换作为位相的变换。由于电磁场的位相在复平面单位圆上是U（1）位相，而单位圆上的两个复数相乘仍在单位圆上，它们形成变换群，即李群。由这种复杂的位相所组成的变换不变性，称为非阿贝尔规范理论，
　　（1）表示法拉第定律和高斯定理，（2）表示安培定律和库仑定律，　
　　从对比中不仅看到了它们之间的相类似之处，而且根据位相概念，很自然地引入了Cijk与Bk?，并用普遍的协变微分替换了普通的微分。
　　本来，在U（1）情况下，一个变换只对应圆周位置上的一个参数，但在复杂的李群情况下，SU（2）需要3个参数，SU（3）需要8个参数，使变换异常复杂起来。虽然电磁力与引力的统一至今没有结果，有一点却是肯定的，它导致了对电磁场是一种位相场的正确认识。一个复杂的位相场就是李群，而复杂的位相所组成的变换不变性即为非阿贝尔规范理论。电磁力与引力的统一应该与非阿贝尔理论紧密相关。
　　非阿贝尔规范理论是在1954年由杨振宁和密耳斯(Mills,R.L.)提出来的。1961年，格拉肖(Glashow,SheldonLee1932～)首先把这一理论用于电磁作用与弱作用的统一。1967年温伯格(Weinberg,Steven1933～)与萨拉姆(Salam,Abdus1926～)又在对称性自发破缺的基础上，提出了电磁与弱相互作用的具体模型，并预言了弱中性流的存在。1970年胡福特(Hooft)等人又将这一模型做了重正化发展。1973年，美国费密实验室与欧洲核子中心相继发现与模型一致的弱中性流。人们确信，非阿贝尔规范场理论不仅是把电、弱，甚至还将是把引力以及强相互作用都统一在内的有力工具。
　　（2）引力的“磁性”研究
　　与引力和电磁力相关性研究相紧密联系的还有关于引力的“磁性”研究。广义相对论的三个经典检验都只涉及引力的“电”分量，即广义相对论中的引力势部分。在牛顿引力理论中，引力只具有“电”分量，它是相对论引力理论在弱引力情况下的近似。然而在广义相对论的理论框架之下，引力应该有其“磁”分量，这一分量与牛顿引力没有近似的对应关系。爱因斯坦在他的转动圆盘中，早就做出过预言，静止的质量只引起引力的“电”分量，而运动的质量将引起引力的“磁”分量，旋转的质量会有引力的“磁矩”，两个运动着的旋转体之间会有引力“磁矩”的相互作用，这些均是牛顿引力理论中所没有的。检验引力的“磁”分量是否存在，自然成为鉴别牛顿引力理论与广义相对论二者的关键之一。
　　检验的原理很简单，用一个在空中旋转的陀螺，根据广义相对论，在旋转的陀螺和旋转的地球之间应该有引力的磁力作用，陀螺会发生进动，进动的方向和进动的速率与地球的旋转有关。这种相互作用与原子物理学中自旋-自旋相互作用十分相似。自旋-自旋相互作用十分微弱，只引起光谱中的谱线的超精细结构。陀螺与地球之间的引力“磁”作用也十分微弱，对一个放置在600千米高空的陀螺，地球引力磁作用，所引起的最大进动率也只有0.044″/年。
　　相对论陀螺实验开始于本世纪80年代，美国斯坦福大学物理系一个实验小组计划在本世纪完成这项实验①。他们的回转仪是一个不球度和不均匀度均极小（相对几何不球度和相对密度不均匀度均小于3×10-7）的熔融石英晶体球，球外由铌超导体覆蔽，并由安放在真空度小于10-8托的高真空石英球腔内的静电装置旋空支撑，整个装置安放在卫星舱内的液氦中，使腔壁冷却温度在9K以下。利用液态氦气流吹动小球，使其转动角速度达到每秒几百转。为了精确地测量到回转仪的进动，必须在无接触条件下，精确地确定回转仪转轴相对卫星的指向。他们选择了七妙的方法，这就是利用磁场进行。当然首先需要对卫星有良好的磁屏蔽，以消除地磁及其它杂散磁场的干扰，它们的强度不得高于10-7高斯数量级。旋转超导球由于伦敦效应被磁化后，磁矩的轴与旋转的轴相垂直，轴的方向可以利用根据约瑟夫森效应工作的高灵敏度超导磁强计测出。这一实验对卫星的要求也很严格。首先它应相对宇宙空间某颗不动的恒星保持定向，定向角度的偏离不得大于0.001拻。为此，装在舱内的定向望远镜镜片应由石英制造，并冷却到液氦温度，在液氦温度下，它们的主光轴由于湿度变化的漂移角度不得超过0.001拻。这一实验的构想新颖，设计巧妙，不仅难度很大，而且应持续数年、十数年甚至数十年才能有明显的结果。在这以前，对广义相对论的检验只涉及引力势的相对修正量测量，即只涉及引力的“电”分量，而这一实验，是从引力的旋度分量，即只涉及引力的“电”分量，而这一实验，是从引力的旋度分量，即从“磁”分量入手进行引力理论的检验，因此它具有十分特殊的地位，世人正以极大的兴趣密切地注视着它的进展。
　　(3)奇性与宇宙监督原理
　　引力场方程在静态球对称真空条件下的史瓦西解是一个精确解，它描述了渐近平直空间中，质量为M的孤立球对称物体的引力场。在通常使用的坐标系中，度规分量在史瓦西半径r=2M处变为奇点。在1959年，经弗伦斯卡尔(Fronskel)、芬克尔斯坦(Finkelstein)及克鲁斯克尔(Kruskal)所证实，这一奇点仅是一个“虚假的”数学奇点，时空结构在这一点所产生的“质变”可以通过坐标系的重新选取而消除。虽然如此，相对性引力理论的奇点问题并未消除。
　　由于引力可以在整个宇宙中产生一种宇观的效应，任何引力理论的发展都会导致对宇宙整体结构的一种解释，随之出现与之相应的一种宇宙模型。牛顿引力理论也如此，然而它所面临的问题是，由这一理论，导致宇宙中的一切物体必须回落到一起，这与当时人们所认为的宇宙基本上不随时间变化的观念相矛盾。广义相对论建成后，爱因斯坦只是靠把宇宙学项硬加到场方程中，才克服了这个“吸引”问题。此外，爱因斯坦的静态宇宙模型仍然是不稳定的，只要有一点微小的扰动，就会使它无休止地塌缩或膨胀起来。1920年，美国天文学家斯里弗(Slipher,VectoMelvin1875～1969)与哈勃(Hubble,EdwinPowell1889～1953）观测到遥远星系的退行以后，爱因斯坦的静态宇宙模型即被人们放弃了，描述膨胀的第一个宇宙模型由美国物理学家弗里德曼(FriedmanHerbert1916～)给出。1922年，弗里德曼的宇宙模型又被罗伯孙(Robertson)与沃克(Walker)所推广，他们的模型假设宇宙是均匀和各向同性的。 1951年，陶伯(Taub)建立了第一个各向异性的宇宙模型，其后又被赫克曼(Heckmann)和舒金(Schuking)所发展。1965年，彭齐阿斯和威尔孙发现了具有高度各向同性的微波背景辐射表明，宇宙的大尺度结构相当近似于弗里德曼模型。很快地，观测得到的宇宙氦和氘的丰度又与弗里德曼模型中的合成计算符合得很好。这些都证明，弗里德曼模型是一个较好的近似宇宙模型。然而，弗里德曼宇宙模型却要求有一个初始奇点，即初始大爆炸产生。
　　 从弗里德曼模型问世时起，回避该模型的奇点研究就一直在进行着。1948年，邦迪(Bondi)、戈尔德(Gold)与霍伊尔(Hoyle)就曾提出宇宙处于稳恒状态，即全部时空点处于相同的面貌，当星系彼此退行时，各时空点的物质也在随时相应地产生，宇宙总保持着密度、状态上的稳恒。这一解释虽然避开了奇点，却与后来的射电源及宇宙微波背景辐射的观测相矛盾。回避奇点的研究还在其它几种途径上进行着，例如，1963年，利弗席兹(Lifshitz)和卡拉特尼科夫(Khalatnikov)把具有奇点的引力场方程解在奇点附近做幂级数展开，他发现，在具有奇点的解中所包含的任意函数比普通解中要少，因而做出推测，具有奇点的解在全部解空间中的测度可能为零。然而后来发现，情况并非如此，在有的普通解中，任意函数仍足够多，奇点仍不可避免。 几十年来的理论研究表明，所有回避奇点的尝试都不太成功。1965年彭罗塞(Penrose)通过整体微分几何证明，如果某些整体性条件得以满足，恒星塌缩过程中的奇点是不可避免的①。彭罗塞的方法又被霍金和杰罗奇(Ceroch)所推广。从1965～1970年间，他们提出了若干理论，并把它们用于宇宙学研究。他们于1970年提出奇点定理②。该定理表明，若满足下列整体条件：①广义相对论正确，②对任何类时向量Va，物质的能动张量满足
　
　　③不存在闭合类时曲线，④任何类时或零测地线上都包含某一点，在该点处有V[aRb]cd[eVf]VcVd≠0，⑤在某点p，使从p发出的指向过去或未来的零测地线再次收敛时，奇点是不可避免的。实际上，在现有的相对论引力理论框架下，上述这五项条件都是合理的。条件①已被若干实验所证实，条件②适用于任何正质量密度和正压力的物质，条件③表明不可能回到自己的过去，这是对因果律的要求，条件④表明，每一条类时或零测地线都会与某些物质或曲率取向无规则的点相遇，条件⑤要求宇宙中的物质或能量足够集中，使从某点p发出的指向过去的每一条光线会聚，这意味着宇宙中存在有足够多的物质，得以使条件⑤满足。
　　奇点定理表明，广义相对论的本身就预言了奇点的存在，因为在一般情况下，每一条类时或零测地线都会存在一个起点。这一定理还表明，当一个恒星收缩到小于史瓦西半径内，就会出现奇点。在奇点处，人们不知道所遵循的规律，丧失了预言未来的能力，而且每一次的恒星塌缩都会在宇宙中增加一个不可知的因素。为摆脱这一困境，人们提出了如下猜想，奇点虽不可避免，但是所形成的奇点是出现在所谓的黑洞范围以内，光线与其它任何信息都不可能从那里逃离出来，人们不能观测到奇性，或奇性与人们日常生活的经典范围不可能发生任何联系，因而物理原则也就不可能被破坏，这一猜想即被称为宇宙监督原理(hypothesis of cosmic censorship)，无论证明或否定这一原理都是相对论引力理论所面临的重要课题之一。参与这一课题研究的有威勒(Wheeler, J. A.)、依斯瑞尔(Israel, W.)、德洛奇克维奇(Doroschkevich, A.G.)、杰尔多维奇(Zel＇dovich Ya.B.)和诺维柯夫(Novikov,S.P.)。
　　（4）量子引力理论
　　20世纪基础物理研究的巨大成就，当归功于相对论、量子论与引力论的建立。相对论、量子论和引力论都具有普适性，它们的普适性的一个重要体现分别表现在c、h和G这三个普适常数上。然而，三个理论是否真的具有普适性，还在于它们彼此间的相容性，广义相对论的建立证实了引力论与相对论的相容性。
　　量子理论的发展证明，物质的各种运动形态都遵从量子化的要求，与此同时，一切相对论性场，如电磁场也应是量子化的。在场量子化研究的初期，曾出现了一系列的发散困难。在40年代末，量子化电磁场的发散困难初步通过重正化理论得以解决。发散困难的最根本解决是在60年代完成。弱电统一理论的建立，不仅解决了弱相互作用中的发散困难，而且在类似弱相互作用的框架之中，还可望在强相互作用领域解决相对论与量子论的相容性。最困难的一步就是引力论与量子论的相容，这一步骤的一个主要目标就是建立量子化的引力理论。量子引力理论的研究还起源于广义相对论的奇点问题。由彭罗塞提出，后经霍金和杰罗奇等人最终建立的奇点定理表明，在相当宽的物态条件下，引力场方程的解必定具有奇性。奇性的存在表明，广义相对论属于服从因果律的经典物理范畴，在奇点处，这一理论不再适用。有可能在考虑到引力场的量子性之后，奇性自然消失，这一猜测随后在霍金黑洞蒸发理论中得到了支持。
　　迫使人们研究量子引力理论的第三个动机来源于大统一理论。弱电统一理论已经建成，弱电与强相互作用的大统一理论正是当前的热门课题，研究过程表明，必须同时考虑到它们与引力作用的统一，而这一统一的实质就是建立量子引力理论。经典物理学的理论框架是建立在因果律的基础上的，经典物理学依赖于物理定律和它相应的边界条件，然而当问题涉及到奇点，而这个奇点又不是数学或模型的缺陷由人为造成的时，奇点很难消除，又很难给出合理的边界条件，这就迫使人们必须重新考虑原有的理论。
　　沿着膨胀和暴涨的宇宙反向历程，应用经典宇宙学所给出的框架，回溯宇宙在暴涨之前的状态，很自然地会得到宇宙的尺度将趋于零。这意味着，引力场的强度以及物质场的能量密度将趋于无限大，宇宙是从一个奇点演化而来的，而这个奇点并非由于模型的缺陷人为引起的。早在60年代，彭罗塞和霍金就曾利用整体微分几何证明过①，奇点不仅是高度对称的，而且是广义相对论的必然产物。这意味着，在广义相对论的理论框架之中，不可能找到解决奇点的方案，或者说，尽管广义相对论揭示了时空的引力弯曲，但它对于极高曲率的空间并不适用。量子论的鼻祖普朗克很早就主张，应在所有的自然力之间建立联系。1899年，他首先提出了“普朗克长度”这一普适的这一最小长度Lp，以后又陆续提出了“普朗克时间”tp、“普朗克温度”Tp与“普朗克质量”Mp，它们分别为Lp=(hG/c3）1/2=4.05×10-33cm, tp=(hG/c5)1/2=1.35×10-43s,Mp=(hc/G)1/2=5.45×10-5g，Tp=(hc5/k2G)1/2=3.56×1032K。由于h、c和G三个常量都是相对论不变量，以它们为基准的普朗克自然单位将是不变和唯一的，这一点具有深刻意义。审查上述量的大小不难看出，温度Tp极高，甚至比宇宙大爆炸时刻的温度还高，长度Lp、时间tp却极小，质量Mp也不很大，虽然这些值都是实验室条件下无法得到的，它们却使人们想到，在暴涨之前的宇宙这些是否是可以接近的尺度，因此，应该由一个量子化的广义相对论取代经典广义相对论。
　　本世纪初，量子力学诞生之后，量子力学原理首先用于解释微小系统——原子结构方面的困难，确立了薛定谔方程，同时也得到了有关原子特征的一系列量子力学描述。本世纪60年代以来，当人们试图用量子力学解释巨大的体系——宇宙结构时，却发现它们之间有着惊人的相似①。首先，在具有电磁作用的质子与电子微小体系中，重要自由度r（t）在趋于零时，产生奇点的经典困难，而在具有引力作用的大物质体系中，重要自由度标度因子R（t）在趋于零时，也产生奇点的经典困难；微小电磁体系具有玻尔半径10-8cm的量子长度，而引力作用体系则具有普朗克长度10-33cm的量子长度；微小体系服从薛定谔方程的动力学规律，而引力体系则有惠勒-德维特方程。关于这两个体系间的相似与联系，近年来的研究又有了新的进展。本世纪60～70年代，德维特(DeWitt,B.S.)、米斯纳(Misner,C.W.)和惠勒等人在量子宇宙学方面做出了重要的基础性工作，他们建立了描述宇宙量子特征的惠勒-德维特方程，然而求解这个方程却面临边界条件的确立。因为最初宇宙究竟处于什么状态仍然不能确定。
　　1967年，德维特曾企图不依靠边界条件，仅仅根据数学上的自冾，得到惠勒-德维特方程的解，即宇宙的波函数①，但是这个愿望最终没能实现。从70年代末到80年代，哈特尔(Har-tle,J.B.)和霍金又提出了一个称为“无边界”的方案②。他们利用40年代由费因曼(R.Feynman)发展起来的路径积分法的量子力学形式，大胆地确定了一个称为无边界条件的宇宙波函数。此外，林德(Linde,A.D.)和维伦京等人又分别提出了“隧道效应”方案，由此得出了称为隧道波函数的宇宙波函数。这两个波函数都表明，宇宙在足够大，即几千个普朗克长度时，时空是经典的，理论结果与观测宇宙学的结果相一致；但当宇宙尺度极小时，宇宙不仅有着极为复杂的拓扑结构，这个结构还不断发生变化，这种变化是起伏的，人们把它形容为“长满了茸毛”的普朗克尺度极早期宇宙，宇宙在“量子茸毛”中创生。尽管到目前为止，尚没有一个成熟的量子引力理论，然而80年代以来，在量子引力课题的研究方面，已经取得了一些有价值的成果。首先，已能较好地说明了均匀性问题。大爆炸宇宙学的均匀性问题曾使人们多年来感到困惑，原因是在宇宙中，各种尺度的星系、星系团、超星系团结构是高密度区，巨洞又是低密度区，宇宙中物质的分布是不均匀的。然而，从微波背景辐射的观测可以看出，各向不同性不超过万分之一，甚至十万分之一，这表明，物质在早期宇宙的分布是均匀的，此外，各种天体氦含量的一致以及不同方向计数结果的一致，也同样表明早期宇宙物质的均匀性。当今宇宙的非均匀性应当从早期的均匀状态演化而来，而非均匀性发展的机制就来自于引力的不稳定性。然而，最初不稳定性的机制来自何处，这正是大爆炸宇宙学的难题之一。原来所提出的热涨落机制已被证明是不存在的，因为这种热涨落所产生的涨落谱，还不能说明当今宇宙所呈现非均匀性的定量特征。
　　80年代以来，在用量子引力理论解释非均匀性起源机制方面，已经取得了一些进展。有两个非均匀性起源的机制理论很有生命力①②。其一是宇宙真空量子涨落，它认为，宇宙年龄在10-36s以前，真空涨落是唯一可能的起伏源。虽然这一涨落只在普朗克常数数量级，但是由于整个暴胀阶段是一个熵增加的耗散过程，初始的量子涨落将具有Ze′ldovich谱，由它可以解释星系成团结构的出现。另一种解释是宇宙弦理论。该理论认为，当温度足够高时，由于自发对称破缺，真空相变起伏，宇宙将出现面、线、点等缺陷。线状宇宙弦还可能重联后，演变成环或弦，它们再吸引物质，就形成各种尺度的天体，这一解释正好又说明了天体分布的自相似性。目前，这两个模型在解释有关星系的条状结构、巨凋结构，星系的亮度，星系、星系团的运动速度、角动量以及3K背景辐射的各向异性、红外背景辐射、引力波背景等方面都取得了不同程度的成功。



相对论与黎曼几何-10-测地线和曲率张量 精选
已有 4757 次阅读 2014-10-9 07:57 |个人分类:系列科普|系统分类:科普集锦
10. 测地线和曲率张量
 
平行移动的概念不仅可以被用来定义曲面的曲率，也可以被用来定义测地线。
 
测地线是欧几里德几何中“直线”概念在黎曼几何中的推广。欧氏几何中的直线，整体来说是两点之间最短的连线，局部来说可以用“切矢量方向不改变”来定义它。将后面一条的说法稍加改动，便可以直接推广到黎曼几何中：
 
“如果一条曲线的切矢量关于曲线自己是平行移动的，则该曲线为测地线。”
 
第八节中曾经给出矢量V平行移动时在列维-齐维塔联络意义下的逆变分量坐标表达式：dVj/ds+ GjnpVndxp/ds= 0。根据上述测地线的定义，如果将其中的Vj用切矢量的分量（dxj/ds）代替的话，便可得到用克里斯托费尔符号表示的测地线的方程。
                                                           
 

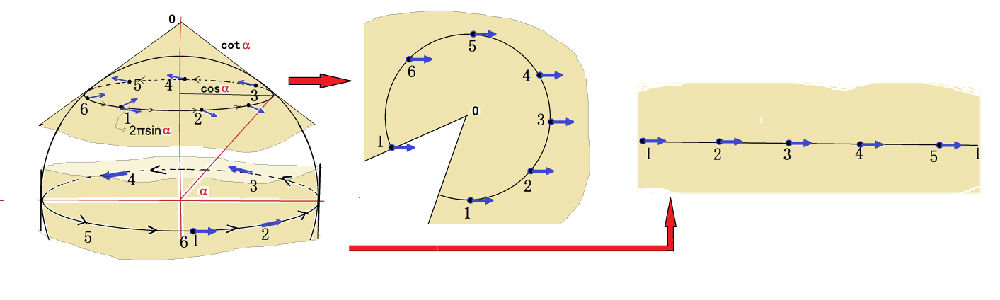
图2-10-1：在纬度a的圆上以及在赤道上切矢量的平行移动有所不同
 
以球面为例，我们可以利用上一节中采取的方法来研究切矢量的平行移动。一般来说，沿着球面上纬度为a的圆的平行移动等效于在一个锥面“帽子”上的平行移动。然而，当a=0时（对应于赤道），锥面变成了柱面，如图2-10-1左图所示。因而，可以将锥面或柱面（赤道）展开成平面来研究球面上的平行移动。图2-10-1中图和右图分别是锥面和柱面展开的平面上平行移动的示意图。。从两个图中可以看出，切矢量的平行移动对a=0（赤道）和a>0（非赤道）两种情形有所不同。对于小于赤道的圆，从锥面展开的平面图可知，点1的切矢量，平行移动到2、3、……各点后不一定再是切矢量；而赤道在柱面展开的平面图中是一条直线，所以，点1的切矢量平行移动到2、3、……各点后仍然是切矢量。
 
因此，如赤道这样的“大圆”，即圆心与球心重合的圆，符合我们刚才所说的测地线的定义：切矢量平行移动后仍然是切矢量。所有的大圆都是球面上的测地线。
 
测地线是否一定是短程线呢？对欧氏空间来说是如此，但对一般的黎曼空间不一定如此。比如球面上，连接两点的测地线至少有两条（一个大圆的两段），那条小于180度的圆弧是短程线，而另一部分，即大于180度的圆弧，就不是短程线了。不过，测地线是局部意义上的短程线，对于充分接近的两个点，测地线是最短曲线。
 
下面继续上一节有关曲率的讨论。
 
如前所述，2维曲面上某一点P的曲率R，被定义为“任意矢量沿曲面上无限小的闭曲线平行移动后的角度亏损对闭曲线所包围之面积的导数”，即：标量曲率R = dq/dA。以上的叙述中包含了如下几点概念：曲率R是局部的，随点P位置的变化而变化；曲率R的定义依赖于一个2维曲面；曲率R的定义与某个角度亏损有关。所谓角度亏损，就是矢量的方向平行移动后相对于原来的方向绕某一个轴转动的角度。
 
在2维曲面上的每个点，按照上面的方法，能定义一个曲率R。也就是说，定义了2维曲面上的一个标量曲率场。
 
现在，如果考虑一般的n维黎曼流形，就需要将上述的曲率概念加以推广。首先想到的是：在维数大于2的流形上的每一点，应该仍然可以局部地定义曲率。然而，如果按照2维曲率定义的方法，当n大于2时，不仅仅得到一个曲率值，而是可以定义多个曲率数值。其原因是因为对高维空间中的一点，通过它的二维面不止一个，另一方面，当我们考虑角度亏损的时候，也不是只有一个角度亏损值，相对于每一个可能存在的转轴，都将有一个所谓角度亏损值。如此一来，n维流形上每一个点的曲率需要不止一个数值来描述。所以，我们便在每个点的切空间中定义一个曲率张量，或换言之，赋予黎曼流形上一个曲率张量场。
 
下面需要考虑的是，这个曲率张量的阶数是多少？或者说，这个曲率张量应该有几个指标，才能表征n维黎曼流形在一个给定点的内蕴弯曲度？
 
图2-10-1：黎曼曲率张量和平行移动
 
可以用如下的方法将2维空间标量曲率概念推广到n维以上的流形。首先考虑n维流形中的矢量V在P点附近的平行移动方式。矢量V可以沿着过P点的任何一个2维子流形的回路平行移动。比如说，图2-10-1所示的是V在由坐标xm和xn表示的曲面上沿着dxm、dxn、-dxm、-dxn围成的四边形回路平行移动的情形。一般来说，当V绕回路一圈返回原点时将和原来矢量不一样，得到了一个改变量dV。类比于标量曲率R的定义，矢量的这个增量应该正比于平行移动的路径所围成的面积，即dxmdxn。除此之外，矢量增量dV还应该与原矢量V有关。考虑dV和V方向上的差异，增量dV的逆变分量dVa可以写成如下形式：
 
dVa= dxmdxnVgRnamg，                                   （2-10-1）
 
这儿，将平行移动一周之后的微小变化用符号d表示，以区别于坐标的线性微分增量dxm或dxn。
 
公式（2-10-1）中的比例系数Rnamg，便是黎曼曲率张量。如前所述，四个指标中的两个m和n对应于平行移动路径所在的2维曲面，而另外两个指标a和g分别表示矢量增量dV及原来矢量V的逆变指标。公式右边的重复指标m、n和g是求和的意思，这是遵循以前提到过的“爱因斯坦约定”，以后用到重复指标时都是表示求和的约定，不再赘述。
 
黎曼曲率张量是个四阶张量，对n维空间，四个指标都可以从1变化到n，因而分量数目很多。但是由于对称性的原因，独立分量的数目大大减少，只有n2(n2-1)/12个。按照这个公式，当n等于4时，有20个独立分量；当n等于2时，曲率只有一个独立分量，这便是我们曾经介绍过的2维曲面的高斯曲率。
 
黎曼几何中有多种方式来理解和定义内在曲率的概念，下面将作一简单介绍。本来是同一个东西，从多种不同的角度看一看可以加深理解。就像是你在观察一座山：“横看成岭侧成峰，远近高低各不同”，多照几张照片才能帮助我们识得庐山真面目。上文中，用平行移动概念来定义的四阶黎曼曲率张量Rnamg是定义曲率最标准的形式。黎曼曲率张量就像是给某座山某处附近照的标准照片，它的4个指标独立地变化，其取值范围都是从1到n，因而总的变化数目就有n4个，在n=4的情形下，这个数等于256。好比是在这附近照了256张照片，不过由于对称性，其中很多是重复的，不重复的只有20张。经专家们研究后认为，将整座山的每一个“局部景观”，都如法炮制地照出20张不重复的照片来，便能够作为这座山的完整描述。


之前，我们也曾经提到过“截面曲率”，它被定义为n维流形过给定点的所有2维截面高斯曲率的总和。截面曲率等效于黎曼曲率张量，与截面曲率有关的20张照片同样也是内蕴曲率的完整描述，但因为拍摄技术有所不同，有着更容易被人理解的直观几何解释。


不过，爱因斯坦在他的引力场方程中用到的，是另外两个称之为里奇曲率的几何量：里奇曲率张量Rμν和里奇曲率标量R，这两个曲率是通过上述黎曼曲率张量的指标缩并而得到的，将指标缩并的意思是什么？继续使用刚才的比喻，20张照片中，有些是相似的，因而可以首先挑选出更有代表性的一类，然后又将此类中的几张照片合并起来放到一张照片中。利用这种技巧，在某种条件下，将20张标准照简化到只用10张就够了。


比如说，里奇曲率张量就是由原来四个指标的黎曼曲率张量Rμaρν，将其中两个指标a和ρ缩并而成的二阶张量，写成：Rμν = Rμρρν。如果将原来黎曼曲率张量中4个指标中的两个（a和ρ）看成是矩阵的行列指标的话，那么，4阶黎曼曲率张量就等效于n2个2阶矩阵。进一步将矩阵的两个行列指标“缩并”：意思就是将这个矩阵只用一个数（它的trace）来表示。因而，指标缩并后，原来的n2个矩阵就变成了n2个数值，这就是所谓的里奇曲率张量。


里奇曲率标量呢，是由里奇曲率张量的两个指标再进一步缩并而成的一个标量：R= gμνRμν。在2维曲面情形下，R正好是高斯曲率的2倍。


这儿最后插上一段话，重申关于对“内蕴”的理解。高斯和黎曼的微分几何研究，强调的也是流形的“内蕴”性质。遗憾的是，受限于大脑的思维能力，我们无法用直观的图像来表达更为高维空间的这种“内蕴”性。唯一能加深和验证理解的直观工具就是想象嵌入在三维欧氏空间中的各种二维曲面。但我们务必要随时记住，在研究这些曲面的几何性质时，尽量不把它们当作三维欧氏空间中的子空间，而是把自己想象成生活在曲面上、只能看见这个曲面上发生的事件的“阿扁”，当我们从阿扁的角度来进行测量、考虑问题时，涉及的几何量便是“内蕴”几何量。然而，阿扁观测到的，只是2维曲面上的内蕴几何，研究维数更高的黎曼流形时，还需要使用另外一个诀窍。这个方法让我们更容易保持“内蕴”的思考，那就是：一切都得从度规张量出发。因为度规张量决定了几何中最基本的内蕴量：弧长，是黎曼几何的关键，有了度规张量后，便可以导出其它的内蕴几何量。
 
理解黎曼几何和广义相对论的另一个重要原则就是，物理规律要与坐标系无关。尽管任何有用处的实际计算都是在某个坐标系下面进行的，但计算结果表达的物理定律却是独立于坐标而存在。这也就是我们总是要将描述物理规律的方程式写成“张量”形式的原因，因为张量的坐标分量在坐标变换下作线性齐次变换。线性表明张量属于切空间，齐次表明张量与坐标系选择无关。如果一个张量在某个坐标系下所有分量都是零，经过线性齐次变换后，它在任何坐标系中都将是零。

在此也顺便回顾和总结下我们介绍黎曼几何的过程。黎曼流形（伪黎曼流形）是定义了一个对称正定（不正定）度规张量场gij的微分流形。为了在黎曼流形上作微分运算，需在相邻点的切空间之间引进“联络”的概念，具体地说，就是用列维-齐维塔联络，将不同切空间中的不同的度规张量关联起来。而作为列维-齐维塔联络坐标表达式的克里斯托费尔符号，只与度规张量和度规张量的微分有关。然后，我们定义了在列维-齐维塔联络意义下的协变微分和平行移动。引进协变微分的目的是为了定义张量之间的微分规则，以确保张量的协变微分仍然是一个张量。因为从协变微分而定义的平行移动与空间的“不平坦”程度密切相关，从而便由平行移动定义了测地线以及各种曲率的概念。


补充：有关平行移动
“如何平行移动”及“角度的变化”都是内蕴观察量，与被嵌入的空间无关。但为了更为直观的说明问题，画出的图只能是嵌入三维空间的二维面，比如下图b中的球面：


上图是在平面和球面上分别作平行移动的例子：女孩从点1到点2再到点3，一直到点7，作平行移动一圈后回到点1（1和7是同一点）。所谓‘平行移动’的意思是说，她在移动的时候，尽可能保持身体（或是她的脸）相对于身体的中心线没有旋转。这样，当她经过1、2、3……回到1的时候，她认为她应该和原来出发时面对着同样的方向。她的想法是正确的，如果她是在平面上移动的话（图a）。但是，假如她是在球面上移动的话，她将发现她面朝的方向可能不一样了！图b中红色箭头所指示的便是她在球面上每个位置时面对的方向。从图中可见，出发时她的脸朝左，回来时却是脸朝右。


下一篇：等效原理




http://blog.sciencenet.cn/blog-677221-834151.html  此文来自科学网张天蓉博客，转载请注明出处。
上一篇：相对论与黎曼几何-9-平行移动和曲率
下一篇：相对论与黎曼几何-11-等效原理

更多
收藏 分享 举报



12 罗德海 应行仁 文克玲 李学忠 黄永义 沈律 许文龙 胡洪涛 qiue jiareng ybyb3929 ychengwei



该博文允许注册用户评论 请点击登录 评论 (9 个评论)



[9]ybyb3929  2014-10-10 08:45
6楼，比较才是数学的基础，正是因为有了方向的比较才有了“矢量”之一概念，而平行移动这些概念是方向比较加运动的结果，而那些所谓“内蕴观察量”是还没有搞明白矢量这一概念的来历的结果。

[8]ybyb3929  2014-10-10 08:39
我的结论就是：测地线是数学家为了忽悠世界人民，将直线偷偷换了概念而制造出了一个像是直线又不是直线的概念而已
博主回复(2014-10-9 18:14)：不是这样的
___________________________我这句“测地线是数学家为了忽悠世界人民”话有点讲过火了，的确数学中存在无意之中偷换概念而造成数学发展出现问题。
没办法，要反数学了，民科不仅反相、反量，还要反数学了。
博主回复(2014-10-9 18:14)：造反派？
————————————————————————
推翻相对论就已得罪不少了人了，本不想再反数学，再得罪更多的人，但又不得不反，因为数学的确出现问题。

[7]张林  2014-10-9 19:03
谢谢补充的内容，我的问题是：平行的定义是相对于自己那个点的局域坐标系而言的，这个局域坐标系是欧氏的吧？她虽然在局域似乎没有转动，但我们整体上在欧氏空间看是转了！内蕴的含义没有想清楚。谢谢张老师
博主回复(2014-10-9 19:21)：平行移动的定义不是相对局域欧氏空间而言的，张量是对欧式空间而定义的。这就是为什么平行移动与联络（克里斯托费尔符号）有关。联络的目的就是将这些不同的欧氏坐标“联络”起来，以便定义微分运算。

[6]张林  2014-10-9 17:04
博文一如既往有货。但对于这个问题一直有个疑惑：矢量的平行移动。在曲面上平行移动一个矢量为什么最后有一个几何角出现。请问这个平行移动是在欧几里德空间中定义的，还是在黎曼空间定义的，平移在黎曼空间应该不存在(还是以欧氏空间看的)，所以似乎这个几何角是欧氏空间的结果，不知道对不对？
博主回复(2014-10-9 18:12)：“如何平行移动”及“角度的变化”都是内蕴观察量，是在黎曼空间里定义的，与被嵌入的欧氏空间无关。见我在文中新加的部分。
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)