https://www.quantamagazine.org/20130917-a-jewel-at-the-heart-of-quantum-physics/
Amplituhedron theory challenges the notion that space-time locality and unitarity are necessary components of a model of particle interactions. Instead, they are treated as properties that emerge from an underlying phenomenon
Amplituhedron
From Wikipedia, the free encyclopedia
An amplituhedron is a geometric structure that enables simplified calculation of particle interactions in some quantum field theories. In planar N = 4 supersymmetric Yang–Mills theory, an amplituhedron is defined as a mathematical space known as the positive Grassmannian.[1]
Amplituhedron theory challenges the notion that space-time locality and unitarity are necessary components of a model of particle interactions. Instead, they are treated as properties that emerge from an underlying phenomenon.[2][3]
The connection between the amplituhedron and scattering amplitudes is at present a conjecture that has passed many non-trivial checks, including an understanding of how locality and unitarity arise as consequences of positivity.[1]
Research has been led by Nima Arkani-Hamed. Edward Witten described the work as “very unexpected" and said that "it is difficult to guess what will happen or what the lessons will turn out to be."[4]
From Wikipedia, the free encyclopedia
An amplituhedron is a geometric structure that enables simplified calculation of particle interactions in some quantum field theories. In planar N = 4 supersymmetric Yang–Mills theory, an amplituhedron is defined as a mathematical space known as the positive Grassmannian.[1]
Amplituhedron theory challenges the notion that space-time locality and unitarity are necessary components of a model of particle interactions. Instead, they are treated as properties that emerge from an underlying phenomenon.[2][3]
The connection between the amplituhedron and scattering amplitudes is at present a conjecture that has passed many non-trivial checks, including an understanding of how locality and unitarity arise as consequences of positivity.[1]
Research has been led by Nima Arkani-Hamed. Edward Witten described the work as “very unexpected" and said that "it is difficult to guess what will happen or what the lessons will turn out to be."[4]
Amplituhedron theory challenges the notion that space-time locality and unitarity are necessary components of a model of particle interactions. Instead, they are treated as properties that emerge from an underlying phenomenon.[2][3]
The connection between the amplituhedron and scattering amplitudes is at present a conjecture that has passed many non-trivial checks, including an understanding of how locality and unitarity arise as consequences of positivity.[1]
Research has been led by Nima Arkani-Hamed. Edward Witten described the work as “very unexpected" and said that "it is difficult to guess what will happen or what the lessons will turn out to be."[4]
Focus: Model Suggests Link between Intelligence and Entropy
Dynamical systems that maximize their future possibilities behave in surprisingly “intelligent” ways.
A. Wissner-Gross/Harvard Univ. & MIT
A. D. Wissner-Gross and C. E. Freer, Phys. Rev. Lett. (2013)
A. D. Wissner-Gross and C. E. Freer, Phys. Rev. Lett. (2013)
In contrast with the usual entropy, no known fundamental law stipulates that this future-looking entropic force governs how a system evolves. But as a thought experiment, the researchers simulated the behavior of simple mechanical systems that included the force, and the effects were profound. For example, a particle wandering in a box did not explore the volume randomly but found its way to the center, where it was best positioned to move anywhere in the box. Another simulation tracked the motion of a rigid pendulum hanging from a pivot that could slide back and forth horizontally. The pendulum eventually moved into an inverted configuration, which is unstable without the modified entropic force. From this upside-down position, the researchers argue, the pendulum can most easily explore all other possible positions.
The researchers interpreted this and other behaviors as indications of a rudimentary adaptive intelligence, in that the systems moved toward configurations that maximized their ability to respond to further changes. Wissner-Gross acknowledges that “there’s no widely agreed-upon definition of what intelligence actually is,” but he says that social scientists have speculated that certain skills prospered during evolution because they allowed humans to exploit ecological opportunities. In that vein, the researchers connect the inverted pendulum’s mechanical “versatility” to the abilities that bipeds like us require in order to make the numerous on-the-fly adjustments needed to stay balanced while walking.
Wissner-Gross and Freer simulated other idealized tasks that mimic standard animal intelligence tests. They emulated “tool use” with a model in which a large disk can gain access to a trapped disk by hitting it with a third disk. Another task, “social cooperation,” required two disks to coordinate their motions. In both cases, the simulated response to the modified entropic force achieved these goals without any further guidance. These two behaviors, along with grammar-driven language, which Wissner-Gross says he also replicated, have been invoked by Harvard’s Stephen Pinker as characteristic of the human “cognitive niche.” “We were quite startled by all of this,” Wissner-Gross says.
Previously, computer scientists have used a version of causal entropy to guide algorithms that adapt to continually updated information. The new formulation is not meant to be a literal model of the development of intelligence, but it points toward a “general thermodynamic picture of what intelligent behavior is,” Wissner-Gross says. The paper provides an “intriguing new insight into the physics of intelligence,” agrees Max Tegmark of MIT, who was not involved in the work. “It’s impressive to see such sophisticated behavior spontaneously emerge from such a simple physical process.”
–Don Monroe
Don Monroe is a freelance science writer in Murray Hill, New Jersey.
A Jewel at the Heart of Quantum Physics
Illustration by Andy Gilmore
Artist’s rendering of the amplituhedron, a newly discovered mathematical object resembling a multifaceted jewel in higher dimensions. Encoded in its volume are the most basic features of reality that can be calculated — the probabilities of outcomes of particle interactions.
Physicists have discovered a jewel-like geometric object that dramatically simplifies calculations of particle interactions and challenges the notion that space and time are fundamental components of reality.
“This is completely new and very much simpler than anything that has been done before,” said Andrew Hodges, a mathematical physicist at Oxford University who has been following the work.
The revelation that particle interactions, the most basic events in nature, may be consequences of geometry significantly advances a decades-long effort to reformulate quantum field theory, the body of laws describing elementary particles and their interactions. Interactions that were previously calculated with mathematical formulas thousands of terms long can now be described by computing the volume of the corresponding jewel-like “amplituhedron,” which yields an equivalent one-term expression.
“The degree of efficiency is mind-boggling,” said Jacob Bourjaily, a theoretical physicist at Harvard University and one of the researchers who developed the new idea. “You can easily do, on paper, computations that were infeasible even with a computer before.”
The new geometric version of quantum field theory could also facilitate the search for a theory of quantum gravity that would seamlessly connect the large- and small-scale pictures of the universe. Attempts thus far to incorporate gravity into the laws of physics at the quantum scale have run up against nonsensical infinities and deep paradoxes. The amplituhedron, or a similar geometric object, could help by removing two deeply rooted principles of physics: locality and unitarity.
“Both are hard-wired in the usual way we think about things,” said Nima Arkani-Hamed, a professor of physics at the Institute for Advanced Study in Princeton, N.J., and the lead author of the new work, which he is presenting in talks and in a forthcoming paper. “Both are suspect.”
Locality is the notion that particles can interact only from adjoining positions in space and time. And unitarity holds that the probabilities of all possible outcomes of a quantum mechanical interaction must add up to one. The concepts are the central pillars of quantum field theory in its original form, but in certain situations involving gravity, both break down, suggesting neither is a fundamental aspect of nature.
In keeping with this idea, the new geometric approach to particle interactions removes locality and unitarity from its starting assumptions. The amplituhedron is not built out of space-time and probabilities; these properties merely arise as consequences of the jewel’s geometry. The usual picture of space and time, and particles moving around in them, is a construct.
“It’s a better formulation that makes you think about everything in a completely different way,” said David Skinner, a theoretical physicist at Cambridge University.
The amplituhedron itself does not describe gravity. But Arkani-Hamed and his collaborators think there might be a related geometric object that does. Its properties would make it clear why particles appear to exist, and why they appear to move in three dimensions of space and to change over time.
Because “we know that ultimately, we need to find a theory that doesn’t have” unitarity and locality, Bourjaily said, “it’s a starting point to ultimately describing a quantum theory of gravity.”
Clunky Machinery
The amplituhedron looks like an intricate, multifaceted jewel in higher dimensions. Encoded in its volume are the most basic features of reality that can be calculated, “scattering amplitudes,” which represent the likelihood that a certain set of particles will turn into certain other particles upon colliding. These numbers are what particle physicists calculate and test to high precision at particle accelerators like the Large Hadron Collider in Switzerland.
The 60-year-old method for calculating scattering amplitudes — a major innovation at the time — was pioneered by the Nobel Prize-winning physicist Richard Feynman. He sketched line drawings of all the ways a scattering process could occur and then summed the likelihoods of the different drawings. The simplest Feynman diagrams look like trees: The particles involved in a collision come together like roots, and the particles that result shoot out like branches. More complicated diagrams have loops, where colliding particles turn into unobservable “virtual particles” that interact with each other before branching out as real final products. There are diagrams with one loop, two loops, three loops and so on — increasingly baroque iterations of the scattering process that contribute progressively less to its total amplitude. Virtual particles are never observed in nature, but they were considered mathematically necessary for unitarity — the requirement that probabilities sum to one.
“The number of Feynman diagrams is so explosively large that even computations of really simple processes weren’t done until the age of computers,” Bourjaily said. A seemingly simple event, such as two subatomic particles called gluons colliding to produce four less energetic gluons (which happens billions of times a second during collisions at the Large Hadron Collider), involves 220 diagrams, which collectively contribute thousands of terms to the calculation of the scattering amplitude.
In 1986, it became apparent that Feynman’s apparatus was a Rube Goldberg machine.
To prepare for the construction of the Superconducting Super Collider in Texas (a project that was later canceled), theorists wanted to calculate the scattering amplitudes of known particle interactions to establish a background against which interesting or exotic signals would stand out. But even 2-gluon to 4-gluon processes were so complex, a group of physicists had written two years earlier, “that they may not be evaluated in the foreseeable future.”
Stephen Parke and Tomasz Taylor, theorists at Fermi National Accelerator Laboratory in Illinois, took that statement as a challenge. Using a few mathematical tricks, they managed to simplify the 2-gluon to 4-gluon amplitude calculation from several billion terms to a 9-page-long formula, which a 1980s supercomputer could handle. Then, based on a pattern they observed in the scattering amplitudes of other gluon interactions, Parke and Taylor guessed a simple one-term expression for the amplitude. It was, the computer verified, equivalent to the 9-page formula. In other words, the traditional machinery of quantum field theory, involving hundreds of Feynman diagrams worth thousands of mathematical terms, was obfuscating something much simpler. As Bourjaily put it: “Why are you summing up millions of things when the answer is just one function?”
“We knew at the time that we had an important result,” Parke said. “We knew it instantly. But what to do with it?”
The Amplituhedron
The message of Parke and Taylor’s single-term result took decades to interpret. “That one-term, beautiful little function was like a beacon for the next 30 years,” Bourjaily said. It “really started this revolution.”
In the mid-2000s, more patterns emerged in the scattering amplitudes of particle interactions, repeatedly hinting at an underlying, coherent mathematical structure behind quantum field theory. Most important was a set of formulas called the BCFW recursion relations, named for Ruth Britto, Freddy Cachazo, Bo Feng and Edward Witten. Instead of describing scattering processes in terms of familiar variables like position and time and depicting them in thousands of Feynman diagrams, the BCFW relations are best couched in terms of strange variables called “twistors,” and particle interactions can be captured in a handful of associated twistor diagrams. The relations gained rapid adoption as tools for computing scattering amplitudes relevant to experiments, such as collisions at the Large Hadron Collider. But their simplicity was mysterious.
“The terms in these BCFW relations were coming from a different world, and we wanted to understand what that world was,” Arkani-Hamed said. “That’s what drew me into the subject five years ago.”
With the help of leading mathematicians such as Pierre Deligne, Arkani-Hamed and his collaborators discovered that the recursion relations and associated twistor diagrams corresponded to a well-known geometric object. In fact, as detailed in a paper posted to arXiv.org in December by Arkani-Hamed, Bourjaily, Cachazo, Alexander Goncharov, Alexander Postnikov and Jaroslav Trnka, the twistor diagrams gave instructions for calculating the volume of pieces of this object, called the positive Grassmannian.
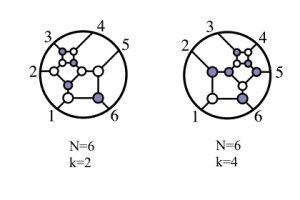
Named for Hermann Grassmann, a 19th-century German linguist and mathematician who studied its properties, “the positive Grassmannian is the slightly more grown-up cousin of the inside of a triangle,” Arkani-Hamed explained. Just as the inside of a triangle is a region in a two-dimensional space bounded by intersecting lines, the simplest case of the positive Grassmannian is a region in an N-dimensional space bounded by intersecting planes. (N is the number of particles involved in a scattering process.)
It was a geometric representation of real particle data, such as the likelihood that two colliding gluons will turn into four gluons. But something was still missing.
The physicists hoped that the amplitude of a scattering process would emerge purely and inevitably from geometry, but locality and unitarity were dictating which pieces of the positive Grassmannian to add together to get it. They wondered whether the amplitude was “the answer to some particular mathematical question,” said Trnka, a post-doctoral researcher at the California Institute of Technology. “And it is,” he said.
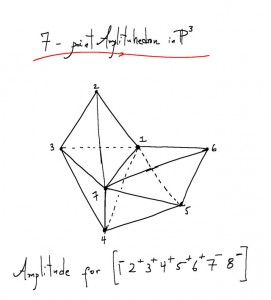Arkani-Hamed and Trnka discovered that the scattering amplitude equals the volume of a brand-new mathematical object — the amplituhedron. The details of a particular scattering process dictate the dimensionality and facets of the corresponding amplituhedron. The pieces of the positive Grassmannian that were being calculated with twistor diagrams and then added together by hand were building blocks that fit together inside this jewel, just as triangles fit together to form a polygon.
Like the twistor diagrams, the Feynman diagrams are another way of computing the volume of the amplituhedron piece by piece, but they are much less efficient. “They are local and unitary in space-time, but they are not necessarily very convenient or well-adapted to the shape of this jewel itself,” Skinner said. “Using Feynman diagrams is like taking a Ming vase and smashing it on the floor.”
Arkani-Hamed and Trnka have been able to calculate the volume of the amplituhedron directly in some cases, without using twistor diagrams to compute the volumes of its pieces. They have also found a “master amplituhedron” with an infinite number of facets, analogous to a circle in 2-D, which has an infinite number of sides. Its volume represents, in theory, the total amplitude of all physical processes. Lower-dimensional amplituhedra, which correspond to interactions between finite numbers of particles, live on the faces of this master structure.
“They are very powerful calculational techniques, but they are also incredibly suggestive,” Skinner said. “They suggest that thinking in terms of space-time was not the right way of going about this.”
Quest for Quantum Gravity
The seemingly irreconcilable conflict between gravity and quantum field theory enters crisis mode in black holes. Black holes pack a huge amount of mass into an extremely small space, making gravity a major player at the quantum scale, where it can usually be ignored. Inevitably, either locality or unitarity is the source of the conflict.
String theory, a framework that treats particles as invisibly small, vibrating strings, is one candidate for a theory of quantum gravity that seems to hold up in black hole situations, but its relationship to reality is unproven — or at least confusing. Recently, a strange duality has been found between string theory and quantum field theory, indicating that the former (which includes gravity) is mathematically equivalent to the latter (which does not) when the two theories describe the same event as if it is taking place in different numbers of dimensions. No one knows quite what to make of this discovery. But the new amplituhedron research suggests space-time, and therefore dimensions, may be illusory anyway.
“We can’t rely on the usual familiar quantum mechanical space-time pictures of describing physics,” Arkani-Hamed said. “We have to learn new ways of talking about it. This work is a baby step in that direction.”
Even without unitarity and locality, the amplituhedron formulation of quantum field theory does not yet incorporate gravity. But researchers are working on it. They say scattering processes that include gravity particles may be possible to describe with the amplituhedron, or with a similar geometric object. “It might be closely related but slightly different and harder to find,” Skinner said.
Physicists must also prove that the new geometric formulation applies to the exact particles that are known to exist in the universe, rather than to the idealized quantum field theory they used to develop it, called maximally supersymmetric Yang-Mills theory. This model, which includes a “superpartner” particle for every known particle and treats space-time as flat, “just happens to be the simplest test case for these new tools,” Bourjaily said. “The way to generalize these new tools to [other] theories is understood.”
Beyond making calculations easier or possibly leading the way to quantum gravity, the discovery of the amplituhedron could cause an even more profound shift, Arkani-Hamed said. That is, giving up space and time as fundamental constituents of nature and figuring out how the Big Bang and cosmological evolution of the universe arose out of pure geometry.
“In a sense, we would see that change arises from the structure of the object,” he said. “But it’s not from the object changing. The object is basically timeless.”
While more work is needed, many theoretical physicists are paying close attention to the new ideas.
The work is “very unexpected from several points of view,” said Witten, a theoretical physicist at the Institute for Advanced Study. “The field is still developing very fast, and it is difficult to guess what will happen or what the lessons will turn out to be.”
Note: This article was updated on December 10, 2013, to include a link to the first in a series of papers on the amplituhedron.
This article was reprinted on Wired.com.
“This is completely new and very much simpler than anything that has been done before,” said Andrew Hodges, a mathematical physicist at Oxford University who has been following the work.
The revelation that particle interactions, the most basic events in nature, may be consequences of geometry significantly advances a decades-long effort to reformulate quantum field theory, the body of laws describing elementary particles and their interactions. Interactions that were previously calculated with mathematical formulas thousands of terms long can now be described by computing the volume of the corresponding jewel-like “amplituhedron,” which yields an equivalent one-term expression.
“The degree of efficiency is mind-boggling,” said Jacob Bourjaily, a theoretical physicist at Harvard University and one of the researchers who developed the new idea. “You can easily do, on paper, computations that were infeasible even with a computer before.”
The new geometric version of quantum field theory could also facilitate the search for a theory of quantum gravity that would seamlessly connect the large- and small-scale pictures of the universe. Attempts thus far to incorporate gravity into the laws of physics at the quantum scale have run up against nonsensical infinities and deep paradoxes. The amplituhedron, or a similar geometric object, could help by removing two deeply rooted principles of physics: locality and unitarity.
“Both are hard-wired in the usual way we think about things,” said Nima Arkani-Hamed, a professor of physics at the Institute for Advanced Study in Princeton, N.J., and the lead author of the new work, which he is presenting in talks and in a forthcoming paper. “Both are suspect.”
Locality is the notion that particles can interact only from adjoining positions in space and time. And unitarity holds that the probabilities of all possible outcomes of a quantum mechanical interaction must add up to one. The concepts are the central pillars of quantum field theory in its original form, but in certain situations involving gravity, both break down, suggesting neither is a fundamental aspect of nature.
In keeping with this idea, the new geometric approach to particle interactions removes locality and unitarity from its starting assumptions. The amplituhedron is not built out of space-time and probabilities; these properties merely arise as consequences of the jewel’s geometry. The usual picture of space and time, and particles moving around in them, is a construct.
“It’s a better formulation that makes you think about everything in a completely different way,” said David Skinner, a theoretical physicist at Cambridge University.
The amplituhedron itself does not describe gravity. But Arkani-Hamed and his collaborators think there might be a related geometric object that does. Its properties would make it clear why particles appear to exist, and why they appear to move in three dimensions of space and to change over time.
Because “we know that ultimately, we need to find a theory that doesn’t have” unitarity and locality, Bourjaily said, “it’s a starting point to ultimately describing a quantum theory of gravity.”
Clunky Machinery
The amplituhedron looks like an intricate, multifaceted jewel in higher dimensions. Encoded in its volume are the most basic features of reality that can be calculated, “scattering amplitudes,” which represent the likelihood that a certain set of particles will turn into certain other particles upon colliding. These numbers are what particle physicists calculate and test to high precision at particle accelerators like the Large Hadron Collider in Switzerland.
United States Postal Service
The iconic 20th century physicist Richard Feynman invented a method for calculating probabilities of particle interactions using depictions of all the different ways an interaction could occur. Examples of “Feynman diagrams” were included on a 2005 postage stamp honoring Feynman.“The number of Feynman diagrams is so explosively large that even computations of really simple processes weren’t done until the age of computers,” Bourjaily said. A seemingly simple event, such as two subatomic particles called gluons colliding to produce four less energetic gluons (which happens billions of times a second during collisions at the Large Hadron Collider), involves 220 diagrams, which collectively contribute thousands of terms to the calculation of the scattering amplitude.
In 1986, it became apparent that Feynman’s apparatus was a Rube Goldberg machine.
To prepare for the construction of the Superconducting Super Collider in Texas (a project that was later canceled), theorists wanted to calculate the scattering amplitudes of known particle interactions to establish a background against which interesting or exotic signals would stand out. But even 2-gluon to 4-gluon processes were so complex, a group of physicists had written two years earlier, “that they may not be evaluated in the foreseeable future.”
Stephen Parke and Tomasz Taylor, theorists at Fermi National Accelerator Laboratory in Illinois, took that statement as a challenge. Using a few mathematical tricks, they managed to simplify the 2-gluon to 4-gluon amplitude calculation from several billion terms to a 9-page-long formula, which a 1980s supercomputer could handle. Then, based on a pattern they observed in the scattering amplitudes of other gluon interactions, Parke and Taylor guessed a simple one-term expression for the amplitude. It was, the computer verified, equivalent to the 9-page formula. In other words, the traditional machinery of quantum field theory, involving hundreds of Feynman diagrams worth thousands of mathematical terms, was obfuscating something much simpler. As Bourjaily put it: “Why are you summing up millions of things when the answer is just one function?”
“We knew at the time that we had an important result,” Parke said. “We knew it instantly. But what to do with it?”
The Amplituhedron
The message of Parke and Taylor’s single-term result took decades to interpret. “That one-term, beautiful little function was like a beacon for the next 30 years,” Bourjaily said. It “really started this revolution.”
Arkani-Hamed et al.
Twistor diagrams depicting an interaction between six gluons, in the cases where two (left) and four (right) of the particles have negative helicity, a property similar to spin. The diagrams can be used to derive a simple formula for the 6-gluon scattering amplitude.“The terms in these BCFW relations were coming from a different world, and we wanted to understand what that world was,” Arkani-Hamed said. “That’s what drew me into the subject five years ago.”
With the help of leading mathematicians such as Pierre Deligne, Arkani-Hamed and his collaborators discovered that the recursion relations and associated twistor diagrams corresponded to a well-known geometric object. In fact, as detailed in a paper posted to arXiv.org in December by Arkani-Hamed, Bourjaily, Cachazo, Alexander Goncharov, Alexander Postnikov and Jaroslav Trnka, the twistor diagrams gave instructions for calculating the volume of pieces of this object, called the positive Grassmannian.
Named for Hermann Grassmann, a 19th-century German linguist and mathematician who studied its properties, “the positive Grassmannian is the slightly more grown-up cousin of the inside of a triangle,” Arkani-Hamed explained. Just as the inside of a triangle is a region in a two-dimensional space bounded by intersecting lines, the simplest case of the positive Grassmannian is a region in an N-dimensional space bounded by intersecting planes. (N is the number of particles involved in a scattering process.)
It was a geometric representation of real particle data, such as the likelihood that two colliding gluons will turn into four gluons. But something was still missing.
The physicists hoped that the amplitude of a scattering process would emerge purely and inevitably from geometry, but locality and unitarity were dictating which pieces of the positive Grassmannian to add together to get it. They wondered whether the amplitude was “the answer to some particular mathematical question,” said Trnka, a post-doctoral researcher at the California Institute of Technology. “And it is,” he said.
Nima Arkani-Hamed
A sketch of the amplituhedron representing an 8-gluon particle interaction. Using Feynman diagrams, the same calculation would take roughly 500 pages of algebra.Like the twistor diagrams, the Feynman diagrams are another way of computing the volume of the amplituhedron piece by piece, but they are much less efficient. “They are local and unitary in space-time, but they are not necessarily very convenient or well-adapted to the shape of this jewel itself,” Skinner said. “Using Feynman diagrams is like taking a Ming vase and smashing it on the floor.”
Arkani-Hamed and Trnka have been able to calculate the volume of the amplituhedron directly in some cases, without using twistor diagrams to compute the volumes of its pieces. They have also found a “master amplituhedron” with an infinite number of facets, analogous to a circle in 2-D, which has an infinite number of sides. Its volume represents, in theory, the total amplitude of all physical processes. Lower-dimensional amplituhedra, which correspond to interactions between finite numbers of particles, live on the faces of this master structure.
“They are very powerful calculational techniques, but they are also incredibly suggestive,” Skinner said. “They suggest that thinking in terms of space-time was not the right way of going about this.”
Quest for Quantum Gravity
The seemingly irreconcilable conflict between gravity and quantum field theory enters crisis mode in black holes. Black holes pack a huge amount of mass into an extremely small space, making gravity a major player at the quantum scale, where it can usually be ignored. Inevitably, either locality or unitarity is the source of the conflict.
Puzzling Thoughts“We have indications that both ideas have got to go,” Arkani-Hamed said. “They can’t be fundamental features of the next description,” such as a theory of quantum gravity.
Locality and unitarity are the central pillars of quantum field theory, but as the following thought experiments show, both break down in certain situations involving gravity. This suggests physics should be formulated without either principle.
Locality says that particles interact at points in space-time. But suppose you want to inspect space-time very closely. Probing smaller and smaller distance scales requires ever higher energies, but at a certain scale, called the Planck length, the picture gets blurry: So much energy must be concentrated into such a small region that the energy collapses the region into a black hole, making it impossible to inspect. “There’s no way of measuring space and time separations once they are smaller than the Planck length,” said Arkani-Hamed. “So we imagine space-time is a continuous thing, but because it’s impossible to talk sharply about that thing, then that suggests it must not be fundamental — it must be emergent.”
Unitarity says the quantum mechanical probabilities of all possible outcomes of a particle interaction must sum to one. To prove it, one would have to observe the same interaction over and over and count the frequencies of the different outcomes. Doing this to perfect accuracy would require an infinite number of observations using an infinitely large measuring apparatus, but the latter would again cause gravitational collapse into a black hole. In finite regions of the universe, unitarity can therefore only be approximately known.
String theory, a framework that treats particles as invisibly small, vibrating strings, is one candidate for a theory of quantum gravity that seems to hold up in black hole situations, but its relationship to reality is unproven — or at least confusing. Recently, a strange duality has been found between string theory and quantum field theory, indicating that the former (which includes gravity) is mathematically equivalent to the latter (which does not) when the two theories describe the same event as if it is taking place in different numbers of dimensions. No one knows quite what to make of this discovery. But the new amplituhedron research suggests space-time, and therefore dimensions, may be illusory anyway.
“We can’t rely on the usual familiar quantum mechanical space-time pictures of describing physics,” Arkani-Hamed said. “We have to learn new ways of talking about it. This work is a baby step in that direction.”
Even without unitarity and locality, the amplituhedron formulation of quantum field theory does not yet incorporate gravity. But researchers are working on it. They say scattering processes that include gravity particles may be possible to describe with the amplituhedron, or with a similar geometric object. “It might be closely related but slightly different and harder to find,” Skinner said.
Courtesy of Jaroslav Trnka
Nima Arkani-Hamed, a professor at the Institute for Advanced Study, and his former student and co-author Jaroslav Trnka, who finished his Ph.D. at Princeton University in July and is now a post-doctoral researcher at the California Institute of Technology.Beyond making calculations easier or possibly leading the way to quantum gravity, the discovery of the amplituhedron could cause an even more profound shift, Arkani-Hamed said. That is, giving up space and time as fundamental constituents of nature and figuring out how the Big Bang and cosmological evolution of the universe arose out of pure geometry.
“In a sense, we would see that change arises from the structure of the object,” he said. “But it’s not from the object changing. The object is basically timeless.”
While more work is needed, many theoretical physicists are paying close attention to the new ideas.
The work is “very unexpected from several points of view,” said Witten, a theoretical physicist at the Institute for Advanced Study. “The field is still developing very fast, and it is difficult to guess what will happen or what the lessons will turn out to be.”
Note: This article was updated on December 10, 2013, to include a link to the first in a series of papers on the amplituhedron.
This article was reprinted on Wired.com.
Add a Comment
View Comments (164)
Both of those issues seem to be stumbling blocks in quantum gravity but I don’t see how it helps to say that “unitarity is not fundamental” without giving an alternative interpretation of the sum over histories approach to QM.
I would frankly prefer that the authors do not make such statements until they do have a consistent framework that gives up on unitarity in particular.
There was a lot of similar talk at the fuzz or fire conference in Santa Barbara and it was equally unsatisfying.
This reminds me of a proposition that reality is a holographic projection on the surface of a hypersphere. The article even mentions, “a master amplituhedron with an infinite number of facets, analogous to a circle in 2-D, which has an infinite number of sides.” Sounds like a hypersphere to me.
Also, regarding gravity, if they’re willing to throw out unitarity and locality, why not gravity? It could equally be a “property that merely arises as consequences of the jewel’s geometry.