www.hongruma.net/wp-content/uploads/2013/02/thermoStat-jidong.pdf
发掘等式1=0.999...中的物理奥义
|||
一只蚂蚁,从坐标原点处往坐标1处爬,它能发现1处的陷阱吗?
高中时期,借得伽莫夫通俗读物《从一到无穷大》一本,很多内容刻尤在骨,封面上的如下一个等式就令人震撼:

近十年来,常有机会面试一些申请或希望进入湖南大学的高三理科生,“如何理解这个等式”之类是我面试题库中的常用题。另一道常用题也出自该书,说有一无限多房间的酒店注满了客人(每房限住一人),可又来了两位客人,还能安排入住吗? 这道题的原始出处据说来自Hilbert.
仅仅学过初等数学,等式1=0.999...不妨这样理解:因为1/3=0.333...,所以1=3x(1/3)=0.999... . 当然,理解不等于证明。初等数学中的一个证明是0.999…=9 x (1/10+1/102+1/103+...)=1.
如果学过高等数学,证明这个等式最高明的方法需要利用到N-ε语言。而涉及这一语言,会遇到两个问题。
问题之一是区间和开和闭。对于半开区间:[0,1) 或者闭区间:[0,1],等式1=0.999...含义不一样。如果一只蚂蚁从0往1爬,对于半开区间,这只蚂蚁不可能到达但是能越来越接近接近1,在x=1这个地方,很可能有一个陷阱;而对于后者,则可以到达。也就是,如果定义一个函数,对于前者,函数是x=1不可能是连续点;对于后者,则有可能。
问题之二有点深奥:在这一点,函数发生了什么事件? 数学上,函数的性质是预先定义好的;在物理上,往往关注一个物理对象,而非抽象的数,例如粒子的运动,一个热力学系统等等。对于这个具体的物理对象能否到达x=1的点,不是一个函数本身就能说清楚,有些问题往往需要通过求导数甚至积分才能看清楚。
所以,弄清函数在x=1处的性质,看似数学,其实能反映出一个物理学家的理论修养。李政道、杨振宁这样的大家由此而创造历史,当然更多的物理教授闹出笑话来而不自知。
一,球与刚性壁间的弹性碰撞
考虑一个质点从x=0处往x=1处匀速地飞,在t=0时与x=1处的刚性壁发生弹性碰撞。位置x对时间t的依赖关系如下:
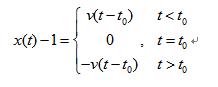
图示如下:
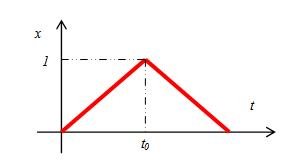
x可以到达1这一点,x本身的定义域为[0,1]. 对x求时间t的导数,得速度:
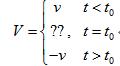
速度空间发生了“灵异”事件:当t=t0时速度无法定义! 也就是从速度空间看,说不清楚粒子有没有到达x=1的点,或者粒子到达后,粒子的速度如何? 图示如下:
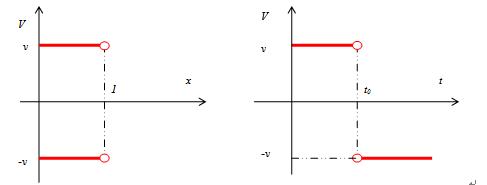
进一步揭示x=1处的奇异性,再求导之。结果出现一个“高等”函数——狄拉克d函数d(t-t0):
a= -2vd(t-t0)= -2v2d(x-1)
也就是出现了一个等效力场:
F=ma= -2vd(t-t0)= -2v2d(x-1)
所谓等效力场,一方面它贡献一个冲量,这个冲量刚好改变粒子的运动方向;另一方面它不做功,W=0!
加速度空间图示结果如下:
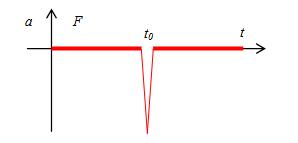
这是一个极其简单的例子,揭示的道理却是深刻的:蚂蚁能爬到1,爬到后会原路返回! 运动是连续的,但是力场确具有奇异性。力场的奇异性通过对运动的求导数就可以揭示出来。
二,杨振宁-李政道定理
给一个连续函数描述水的流体态,谁是天皇老子能告诉我这个函数何时水处在气相还是液相? 杨-李单位圆定理(西方作者往往称之李-杨定理)是李杨合作的最高成就之一,他们二人的天才在于准确理解了通过求导发现函数奇异性的道理,从而解决了上述问题。
设一个(配分)函数为:
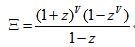
这个函数z=1为可除奇点,也就是它本身完全是一个连续函数。这个函数类似于上例中位置x和时间t的关系。
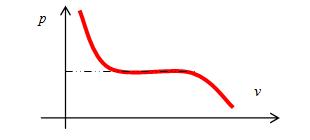
物态方程是压强p和温度T和(单位质量物质的)体积v间的关系。固定好温度T,考察p和v之间的关系,需要对z求一阶导数。步骤如下:
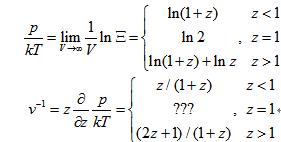
和上面速度v对时间的依赖关系何其相似,“灵异”再次出现:体积v在z=1处不连续!
将z反解出来依赖于v,立即得到一级相变结果:
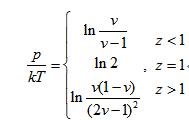
图示结果如下
不但蚂蚁能爬到1,爬到后蚂蚁居然变成了金刚。这个变化也是通过求导数才能看出来。
三,一个贻笑大方的故事
2005年,长沙理工大学物理系有位本科生写信给《物理学报》,指出该刊当年发表的计算三维各向同性谐振子能级的论文有误。《物理学报》对这类稿子通常的处理是:1,原文发表也是请专家评审过的,专家那么容易出错? 2.作者私下沟通一下算了,公开发表“comment”就免了吧。一篇彻头彻尾的错误论文就留在那里至今无人公开指出来。刊物的这种做法其实很不严肃,至少会导致内行对这份刊物权威性的怀疑。
我常有幸看到了论文作者(一位正教授)和那位本科生之间等的若干通讯。作为一名量子力学研究者,我非常佩服那位教授的胆量:对于三维各向同性谐振子能级这种过分熟悉体系的本质上的新发现,发表之前是否要扪心自问一番?
教授的新发现基于建议在r=0点的波函数Y应当满足rY有限,而不是Y本身有限,进而发现一个基态比大家熟悉的基态还要低。除了r=0点,体系的薛定谔方程中的势能的确是各向同性谐振子势能,但是,对波函数求两阶导数,立即发现r=0点出现了一个d函数势能。而三维各向同性谐振子中心带有d函数势能的情况,曾谨言先生已经给出正确处理的途径,那位教授的方法也不对。
在这个例子中,眼睁睁看到蚂蚁靠近1,然后跌到1处的沟里去了。呵呵。
http://blog.sciencenet.cn/blog-3377-537780.html 此文来自科学网刘全慧博客,转载请注明出处。
上一篇:教师对教材内容是否应该有点洁癖?
下一篇:如何利用自主招生平台发现优秀的准大学生?
46 苏力宏 吕喆 李学宽 刘艳红 武夷山 田灿荣 吴吉良 张小平 曹聪 黄秀清 谢鑫 王喜军 许浚远 梁建华 李泳 林涛 王春艳 陈威华 张文卓 王修慧 曹宇 马红孺 王涛 苏德辰 袁君云 张勇洪 刘庆丰 许先进 彭泉 王萌杰 程智 李志军 白图格吉扎布 肖赛君 鲍得海 曹广福 吴中祥 齐伟 占礼葵 李贵发 ZeroK paulings guoyanghuawu qinmingyan hshnxyj wpsuper
发表评论 评论 (27 个评论)
- [27]程中州
- 呵呵,其实蚂蚁是不知道怎么就掉进1里去的,非但蚂蚁不知道,我们也不知道,不管是计算还是极限,都只能得出最终结果:真掉进去了哎,怎么掉的,不知道~这应该是个哲学问题(芝诺悖论),非数学物理所能解决也~
- 博主回复(2014-4-9 20:35):哲学和数学物理间,的确有距离。

- [26]白图格吉扎布
- 有意思。链接到普兰塔。
- [25]sechu
- 证明0.999…=9 x (1/10+1/102+1/103+...)=1不是初等证明。最后一个等号用到了高等数学的极限。
- [24]吴胜平
- 糊涂虫 华罗庚 教出来的学生
- [23]胡大伟
- 从极限的观点来看1就=0.9999999999... ... ...,
- [22]刘新建
- 我的理解:这是理论与现实的差异!现实中是不存在准确的0.9999999……,因为你在既定的1的定义下永远无法准确用仪器测量到。1=0.9999999……是理论的,是一定意义下的相等!
- [21]梁智鹏
- 1=0.9999……,涉及到“=”这个符号的定义。它本来用于两个有限自然数之间比较,就是“一一对应”的意思;即使后来推广到有理数,也是基于有限多次的一一比较。但是在本题中,涉及到无限多次(数位的)比较,因此它能否这样用还存在疑问(就像无穷级数的收敛性一样需要证明)。
另外,本题等号两边是相等的,而写法不一样,这表明了我们进位记数法在涉及到无穷时的一个bug——不一致性。但这也无可奈何,因为“完备的就是不一致的”嘛。
- [20]薛堪豪
- 要是被刘老师面试这题,我肯定说:实数系是稠密的,两个不相等的实数之间有无穷多的其他实数。不断等分就可以了。但 1 和 0.99999... 之间塞不下其他东西,所以它们就是一回事,也就是绝对相等,就是实轴那同一个点。不知能够过关。
- 博主回复(2012-2-27 00:00):绝对相等? 似乎不是!

- [19]吴中祥
- 只提一点!
1不=而只是趋近于0.9999999999... ... ...,
此处的=只有如此而已理解才对,否则就会出现场矛盾! - 博主回复(2012-2-27 00:00):谢谢吴老!
- [18]李鹏程
- 原来曾谨言的《量子力学导论》6.1.2谈到了这个问题。。。顺便还查到他在1989年《大学物理》《薛定谔方程的解在r=0邻域的行为》中还专门提到了谐振子的情况。。。以前学的时候全没注意这些问题,惭愧。。。
- 博主回复(2012-2-19 20:25):知识在于积累,现在知道并不迟啊。

- [17]李鹏程
- 您是指如果基态波函数径向部分是exp(-r^2/2)/r的话不满足谐振子势的薛定谔方程吗?
- 博主回复(2012-2-19 17:42):这个波函数当然不满足谐振子势,而是谐振子势+c delta(r). 回想一下点电荷的电势满足的方程吧。

- [16]李鹏程
- 物理小站:http://zhan.renren.com/physpace?from=rrsearch&checked=true
谐振子那篇文章是否是 基态球谐振子的空间"塌陷"? - 博主回复(2012-2-17 19:51):谢谢提供链接。

您所指论文,您自己有何看法?
No comments:
Post a Comment