求圆弧长计算公式?_数学_作业_天涯问答
wenda.tianya.cn/question/52112013b090977c
轉為繁體網頁
2009年2月18日 - 弧长的定义:一段弧的长度叫做弧长。 弧长的计算公式:在半径是R的圆中,因为360°轉為繁體網頁
【转】弧度和角度的转换
2014-07-25 09:28 by xiashengwang, 1122 阅读, 0 评论, 收藏, 编辑
这两天在看同事写的四叉树代码,其中用到了孤度和角度之间的转换,所以转载此文章进行了学习
“ 弧度”和“度”是度量角大小的两种不同的单位。就像“米”和“市尺”是度量长度大小的两种不同的单位一样。
在flash里规定:在旋转角度(rotation)里的角,以“度”为单位;而在三角函数里的角要以“弧度”为单位。这个规定是我们首先要记住的!!!例如:rotation2--是旋转“2度”;sin(π/2)--是大小为“π/2弧度”的角的正弦。
二、弧度的定义
所谓“弧度的定义”就是说,1弧度的角大小是怎样规定的?
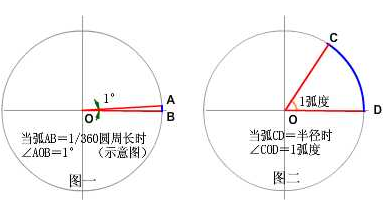
我们知道“度”的定义是,“两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆周长的360分之一时,两条射线的夹角的大小为1度。(如图1)
那么,弧度又是怎样定义的呢? 弧度的定义是:两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时,两条射线的夹角大小为1弧度。(如图2)
比较一下,度和弧度的这两个定义非常相似。它们的区别,仅在于角所对的弧长大小不同。度的是等于圆周长的360分之一,而弧度的是等于半径。
简单的说,弧度的定义是,当角所对的弧长等于半径时,角的大小为1弧度。
此主题相关图片如下:
角所对的弧长是半径的几倍,那么角的大小就是几弧度。
它们的关系可用下式表示和计算:
角(弧度)=弧长/半径
圆的周长是半径的 2π倍,所以一个周角(360度)是 2π弧度。
半圆的长度是半径的 π倍,所以一个平角(180度)是 π弧度。
三、度跟弧度之间的换算
据上所述,一个平角是 π 弧度。
即 180度=π弧度
由此可知:
1度=π/180 弧度 ( ≈0.017453弧度 )
因此,得到 把度化成弧度的公式:
弧度=度×π/180
例如:
90°=90×π/180 =π/2 弧度
60°=60×π/180 =π/3 弧度
45°=45×π/180 =π/4 弧度
30°=30×π/180 =π/6 弧度
120°=120×π/180 =2π/3 弧度
反过来,弧度化成度怎么算?
因为 π弧度=180°
所以 1弧度=180°/π (≈57.3°)
因此,可得到 把弧度化成度的公式:
度=弧度×180°/π
例如:
4π/3 弧度=4π/3 ×180°/π
= 240°
也许有些朋友会说,究竟是乘以“π/180 ”,还是“180°/π”很容易搞错。其实你只要记住:π是π弧度,180是180度。我要化成什么单位,就要把有这个单位的放在分子上。也就是说我要化成弧度,就要把π弧度放在分子上--乘以π/180 。另外,1度比1弧度要小得多,大约只有0.017453弧度(π/180≈0.017453)。所以把度化成弧度后,数字肯定要变小,那么化弧度时一定是乘以π/180 了。能够这样想一想,就不会搞错了。
在AS代码里把“π”写成“PI”。又因为“π”、“sin”都是“数学函数”,按规定要在前面加上“Math.”(Math是英语中“数学”Mathematics的缩写),加上后写成“Math.PI”、“Math.sin”。
所以 sin30°就得写成 Math.sin(30*Math.PI/180)。其中小括弧内的部分是把30°化为弧度,即30×π/180 。
弧度与角度的关系
一、角的两种单位“ 弧度”和“度”是度量角大小的两种不同的单位。就像“米”和“市尺”是度量长度大小的两种不同的单位一样。
在flash里规定:在旋转角度(rotation)里的角,以“度”为单位;而在三角函数里的角要以“弧度”为单位。这个规定是我们首先要记住的!!!例如:rotation2--是旋转“2度”;sin(π/2)--是大小为“π/2弧度”的角的正弦。
二、弧度的定义
所谓“弧度的定义”就是说,1弧度的角大小是怎样规定的?
我们知道“度”的定义是,“两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆周长的360分之一时,两条射线的夹角的大小为1度。(如图1)
那么,弧度又是怎样定义的呢? 弧度的定义是:两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时,两条射线的夹角大小为1弧度。(如图2)
比较一下,度和弧度的这两个定义非常相似。它们的区别,仅在于角所对的弧长大小不同。度的是等于圆周长的360分之一,而弧度的是等于半径。
简单的说,弧度的定义是,当角所对的弧长等于半径时,角的大小为1弧度。
此主题相关图片如下:

角所对的弧长是半径的几倍,那么角的大小就是几弧度。
它们的关系可用下式表示和计算:
角(弧度)=弧长/半径
圆的周长是半径的 2π倍,所以一个周角(360度)是 2π弧度。
半圆的长度是半径的 π倍,所以一个平角(180度)是 π弧度。
三、度跟弧度之间的换算
据上所述,一个平角是 π 弧度。
即 180度=π弧度
由此可知:
1度=π/180 弧度 ( ≈0.017453弧度 )
因此,得到 把度化成弧度的公式:
弧度=度×π/180
例如:
90°=90×π/180 =π/2 弧度
60°=60×π/180 =π/3 弧度
45°=45×π/180 =π/4 弧度
30°=30×π/180 =π/6 弧度
120°=120×π/180 =2π/3 弧度
反过来,弧度化成度怎么算?
因为 π弧度=180°
所以 1弧度=180°/π (≈57.3°)
因此,可得到 把弧度化成度的公式:
度=弧度×180°/π
例如:
4π/3 弧度=4π/3 ×180°/π
= 240°
也许有些朋友会说,究竟是乘以“π/180 ”,还是“180°/π”很容易搞错。其实你只要记住:π是π弧度,180是180度。我要化成什么单位,就要把有这个单位的放在分子上。也就是说我要化成弧度,就要把π弧度放在分子上--乘以π/180 。另外,1度比1弧度要小得多,大约只有0.017453弧度(π/180≈0.017453)。所以把度化成弧度后,数字肯定要变小,那么化弧度时一定是乘以π/180 了。能够这样想一想,就不会搞错了。
在AS代码里把“π”写成“PI”。又因为“π”、“sin”都是“数学函数”,按规定要在前面加上“Math.”(Math是英语中“数学”Mathematics的缩写),加上后写成“Math.PI”、“Math.sin”。
所以 sin30°就得写成 Math.sin(30*Math.PI/180)。其中小括弧内的部分是把30°化为弧度,即30×π/180 。
关于圆的周长和面积的由来,为什么说圆周率乘以直径就是周长,为什么说圆周率乘以半径的平方就是面积?想知道理论的推导和证明。
非数学专业,只是非常想知道,希望答案通俗易懂,谢啦
3个答案
圆周率的最初定义就是周长除以直径。
关于面积为什么是"圆周率乘以半径的平方",有一种比较直观又不失严谨的解释方法:

如图,把圆周切割成N等份,当N很大,每一份近似一个三角形,分别计算面积,就是【弧长×半径/2】,将这N等份的面积求和,就是【周长×半径/2】,也就是【圆周率乘以半径的平方】。
【题外科普】
以上是最基础的中学几何内容,其实圆周率是非常神奇、非常体现数学艺术感的东西,不只是和圆有关,它经常出现在和几何无关的场合,参见:《Pi究竟牛B在哪里?》
关于面积为什么是"圆周率乘以半径的平方",有一种比较直观又不失严谨的解释方法:

如图,把圆周切割成N等份,当N很大,每一份近似一个三角形,分别计算面积,就是【弧长×半径/2】,将这N等份的面积求和,就是【周长×半径/2】,也就是【圆周率乘以半径的平方】。
【题外科普】
以上是最基础的中学几何内容,其实圆周率是非常神奇、非常体现数学艺术感的东西,不只是和圆有关,它经常出现在和几何无关的场合,参见:《Pi究竟牛B在哪里?》
第一个问题:
可以认为圆周率就是这么定义的:圆周率=圆周长/直径.
第二个问题:
小学课本上给的解释,应该是五年级左右(五年制小学),手头没有课本只搜到以下链接,
http://wenku.baidu.com/view/de10ab1214791711cc791703.html
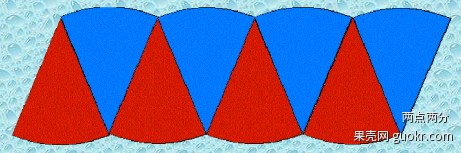
把圆切开了组成以上图形,切的越多越接近长方形.这个长是周长的一半也就是 pi*r/2,宽是r,面积长*宽也就是
pi*r/2 * r
可以认为圆周率就是这么定义的:圆周率=圆周长/直径.
第二个问题:
小学课本上给的解释,应该是五年级左右(五年制小学),手头没有课本只搜到以下链接,
http://wenku.baidu.com/view/de10ab1214791711cc791703.html

把圆切开了组成以上图形,切的越多越接近长方形.这个长是周长的一半也就是 pi*r/2,宽是r,面积长*宽也就是
pi*r/2 * r
这个问题其实问得很好
提问者的问题其实应该转变一下,是否圆的周长除以圆的直径是一个定值?
这个就涉及到古希腊数学史上的最著名的证明,即阿基米德的证明
阿基米德的证明实际上还是用多边形去不断的逼近一个圆----祖冲之也是这么做的,实际上圆就可以理解为一个无穷多边形。
阿基米德证明以N边形逼近圆,不管N等于多少,其周长与N边形的“半径”的长度的比值都是确定的,因而当逼近到无穷多边形的时候,其比值也就是一定的。
算面积也是一样,用N边形的面积去逼近圆的面积。
你可以去百度搜索一下阿基米德和圆周率
阿基米德被认为是与牛顿欧拉高斯们地位相等的伟大的数学家,显然只有浮力定律,杠杆原理等等静力学方面的贡献是不能称作为数学家的
刚才在网上稍微搜索了一下,中文网络对阿基米德关于圆周率的贡献仅仅提到了计算圆周率的贡献,实际上他更大的贡献在于用严谨的证明方法证明了这是一个定值。
反过来说,祖冲之他们并没有证明周长半径比是一个定值,其思维的严谨性是远不如阿基米德等古希腊人的
提问者的问题其实应该转变一下,是否圆的周长除以圆的直径是一个定值?
这个就涉及到古希腊数学史上的最著名的证明,即阿基米德的证明
阿基米德的证明实际上还是用多边形去不断的逼近一个圆----祖冲之也是这么做的,实际上圆就可以理解为一个无穷多边形。
阿基米德证明以N边形逼近圆,不管N等于多少,其周长与N边形的“半径”的长度的比值都是确定的,因而当逼近到无穷多边形的时候,其比值也就是一定的。
算面积也是一样,用N边形的面积去逼近圆的面积。
你可以去百度搜索一下阿基米德和圆周率
阿基米德被认为是与牛顿欧拉高斯们地位相等的伟大的数学家,显然只有浮力定律,杠杆原理等等静力学方面的贡献是不能称作为数学家的
刚才在网上稍微搜索了一下,中文网络对阿基米德关于圆周率的贡献仅仅提到了计算圆周率的贡献,实际上他更大的贡献在于用严谨的证明方法证明了这是一个定值。
反过来说,祖冲之他们并没有证明周长半径比是一个定值,其思维的严谨性是远不如阿基米德等古希腊人的
No comments:
Post a Comment