http://www.eaglefantasy.com/archives/386

庞加莱的几何学

最近在看庞加莱（Poincaré）（又被翻译成彭加勒）的《科学与假设》，这是一本闪耀着思想光辉的圣书。介绍科学知识的书很多很多，但是像《科学与假设》这种写科学哲学的书恐怕很难找得到。虽然这本书的语言非常艰涩难懂，但这本书我至少读过3遍，每一遍都能读出一些新的感悟。
在这本书里，庞加莱对几何学提出了几条思想很深刻的见解：
1.几何学公理既非综合判断，也非实验经验，他们是约定。约定是心智的产物，约定的选择是自由的，但又不是随意的。
2.假使自然界没有固体，便不会有几何学。欧几里德几何学的性质与天然固体非常符合。
3.欧几里德几何学不比非欧几何学更真，他只是更为方便而已。经验在任何时候都不会与欧几里德共设相矛盾，同样任何经验永远也不会和罗巴切夫斯基共设相矛盾。
4.可以建立一本词典，把非欧几何的术语和欧几里德几何的术语之间建立一一对应的关系，这样非欧几何将永远不会和欧几里德几何相矛盾。
5.实验告诉我们的是物体之间的相互关系；至于物体与空间的关系，或者空间个部分的互相关系，没有一个实验影响或者能够影响。实验与空间无关，而与物体有关。
为了对非欧几何加以诠释，庞加莱在这本书里提到了著名的庞加莱圆盘模型，这个模型是非常有意思的：

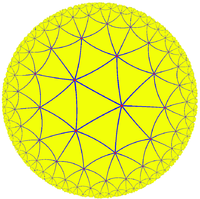
假定有一个用大球包围起来的世界，他服从下述定律：（1）温度不是均匀的，在中心温度最高，随着距中心距离的增大，温度成比例的减小，当接近包围这个世界的球面时，温度降至绝对零度。更精确的表述为：设R为包围这个世界的球的半径，r是所考虑的点到中心的距离，则绝对温度将与R^2-r^2成正比。（2）这个世界上一切物体具有同一膨胀系数，从而任何量尺的长度都与他的绝对温度成比例。（3）假定一物体从一点移动到另一点时，他能立即与新环境处于热平衡。（4）这个世界充满了光的折射媒介质，折射率与R^2-r^2成反比。以上这些假设，没有什么是矛盾的或不可想象的。直观的图形可以参见左图。这就是非欧几何的一种。
从我们通常的几何学观点来看，这个世界是有限的，但对于这个世界的居民来说，它却是无限的。因为当居民试图接近有限球面时，他们逐渐变冷因而变得越来越小，他们迈出的步子越来越小从而永远达不到有限球面。
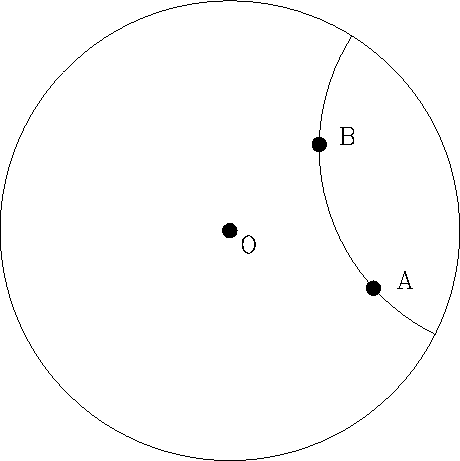
由假定（1）可以推算出来在这个世界中最短路径不是直线，而是圆弧，这圆弧将垂直于边界。假定（4）则保证了光的物理性质：光总走光程最短的路线，从而保证这个世界的居民对光的研究和对固体的研究是一致的。
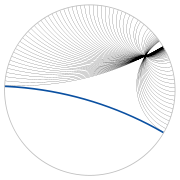
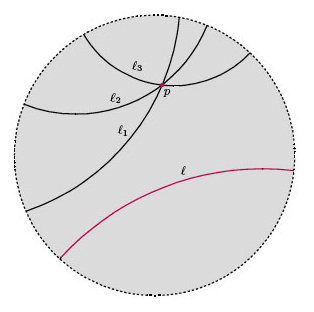
说这个世界是非欧几何，最主要的证据是它违反了欧几里德的第五共设。注意，在庞加莱模型中过“直线”外一点可以做出无数条与该直线平行的“直线”。为了搞清楚这句话的确切意思，我们需要明确一下“直线”的定义，“直线”指的是过两点的最短路径，所以在此模型中“直线”就是连接两点并且垂直于边界的圆弧。
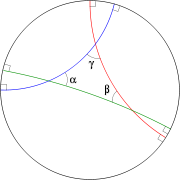
还应该注意，在这个模型中三角形的内角和小于180度。