球面波方程的形式不随空间坐标系统的转动而变化，所以可以将它写成仅与距源点距离r 相关的函数。方程的三维形式,我们生活的空间是三维的，所以我们可以清晰地通过声波和电磁波（都属于球面波）来互相交流

标量形式的三维波动方程
三维波动方程初值问题的解可以通过求解球面波波动方程得到。求解结果可用于推导二维情况的解。

[编辑] 球面波

球面波方程的形式不随空间坐标系统的转动而变化，所以可以将它写成仅与距源点距离r 相关的函数。方程的三维形式为：

将方程变形为：

此时，因变量ru 满足一维波动方程，于是可以利用达朗贝尔行波法将解写成：

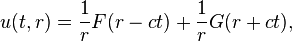
其中F 和G 为任意函数，可以理解为以速度c 从中心向外传播的波和从外面向中心传播的波。这类从点源传出的波强度随距点源距离r 衰减，并且属于无后效波，可以清晰地搭载信号。这种波仅在奇数维空间中存在（原因将在下一小节中详细解释）。幸运的是，我们生活的空间是三维的，所以我们可以清晰地通过声波和电磁波（都属于球面波）来互相交流。