恩...最后ls说的应该是幺正算符，既符合幺正变换的算符
谣言粉碎机
死理性派
谋杀 现场 法医
性 情
心事鉴定组
健康朝九晚五
自然控
创意科技
DIY
美丽也是技术活
微科幻
环球科技观光团
科技视点
文艺科学
爱宠
科技与商业波函数里面的虚数部分作何解释？
2012-01-15 00:27:56
RT.为什么波函数非要是一个复值函数呢，它里面的虚数部分有什么物理含义呢？为什么每次计算概率的时候其实是取波函数的模？如果一开始就把它定为实值的，不就不用这么麻烦了？？？。。。。。
45条回应
- 2012-01-15 02:03:08Derr
1楼不能单单看虚数部分啊，复数可以表示成R Exp的嘛引用
R的平方就是概率，theta代表波函数的相位啊 - 2012-01-15 02:13:55Uroboros2楼引用引用@Derr的回应：不能单单看虚数部分啊，复数可以表示成R Exp的嘛
R的平方就是概率，theta代表波函数的相位啊
所以这里就是奇怪的地方啊。。。为什么不直接取概率呢？？技术上来说，完全可以构造一个实值的符合实验数据的波函数啊。。。。ψ(x,t)难道不能直接表示为概率P(x,t)吗，为什么非要用ψ(x,t)ψ*(x,t)来表示P(x,t)呢？？？？ - 2012-01-15 02:30:39Derr3楼这是希尔伯特空间里面内积定义的吧，本身薛定谔方程求解就是在复数域，所以求出来的方程自然而然会含有复数哇引用
其实实际应用里面人们一般都会忽视掉相位直接求概率的 - 2012-01-15 05:16:43Maigo 语言爱好者 ψ
4楼引用引用@Uroboros的回应：
所以这里就是奇怪的地方啊。。。为什么不直接取概率呢？？技术上来说，完全可以构造一个实值的符合实验数据的波函数啊。。。。ψ(x,t)难道不能直接表示为概率P(x,t)吗，为什么非要用ψ(x,t)ψ*(x,t)来表示P(x,t)呢？？？？
单就某个时刻来看，确实只需要模就能确定概率。
但是这个模函数随时间变化的规律不容易表达，而用复数形式的波函数就容易表达了。 - 2012-01-15 14:12:26Uroboros5楼引用引用@Maigo的回应：
单就某个时刻来看，确实只需要模就能确定概率。
但是这个模函数随时间变化的规律不容易表达，而用复数形式的波函数就容易表达了。
也就是说完全是为了从数学上操作薛定谔方程更容易而使用的一个数学技巧。。。本身并没有什么物理含义？。。。。。 - 2012-01-15 14:25:31Maigo 语言爱好者 ψ6楼引用引用@Uroboros的回应：
也就是说完全是为了从数学上操作薛定谔方程更容易而使用的一个数学技巧。。。本身并没有什么物理含义？。。。。。
你要这么说也行…… - 2012-01-15 14:37:30Uroboros7楼引用引用@Maigo的回应：
你要这么说也行……
难道还有其他的解释？？。。。 - 2012-01-15 23:34:07Maigo 语言爱好者 ψ8楼引用引用@Uroboros的回应：
难道还有其他的解释？？。。。
只是觉得这么说有点太露骨了…… - 2012-02-02 23:36:24逻辑谬误
9楼引用引用@Uroboros的回应：
所以这里就是奇怪的地方啊。。。为什么不直接取概率呢？？技术上来说，完全可以构造一个实值的符合实验数据的波函数啊。。。。ψ(x,t)难道不能直接表示为概率P(x,t)吗，为什么非要用ψ(x,t)ψ*(x,t)来表示P(x,t)呢？？？？
就是不行啊。这样的ψ(x,t)的概率流会不守恒。你可以试用实值函数来概括实验，你会发现是做不到的。例如双缝实验就是平方的时候干涉形就是来自两个波函数的交叉项。
最重要的是波函数是薛定諤方程式的解。所以必须是复值的。因为定態随时间的演化就是乘上一个复数相位。也就是说如果t=0的时候波函数是实值、在下一个就不再是了。复值函数是不可避免的。除非你先否定薛定諤方程式。 - 2012-02-02 23:44:26Uroboros10楼引用引用@逻辑谬误 的回应：
就是不行啊。这样的ψ(x,t)的概率流会不守恒。你可以试用实值函数来概括实验，你会发现是做不到的。例如双缝实验就是平方的时候干涉形就是来自两个波函数的交叉项。
最重要的是波函数是薛定諤方程式的解。所以必须是复值的。因为定態随时间的演化就是乘上一个复数相位。也就是说如果t=0的时候波函数是实值、在下一个就不再是了。复值函数是不可避免的。除非你先否定薛定諤方程式。
因该是先有波函数的数学模型，后才有薛定谔方程的吧？整个方程本来就是建立在波函数的公设之上的。。。。假如一开始就把波函数弄成实值的，那么可能会导出另外一种类似薛定谔方程的方程（或者根本就导不出。。。）。。。话说，实值的时候也是可以干涉的，经典的波不就是这么干涉的吗？？。。。。。 - 2012-02-03 03:05:00逻辑谬误11楼引用引用@Uroboros的回应：
因该是先有波函数的数学模型，后才有薛定谔方程的吧？整个方程本来就是建立在波函数的公设之上的。。。。假如一开始就把波函数弄成实值的，那么可能会导出另外一种类似薛定谔方程的方程（或者根本就导不出。。。）。。。话说，实值的时候也是可以干涉的，经典的波不就是这么干涉的吗？？。。。。。
薛定谔方程式和复数波函数都是公设之一，不能说那条更根本。
波函数的模和相都有分别物理意义。后者影响阿哈罗诺夫－玻姆效应。所以你不能用只有一个值的实函数代替两个值。
另外一点是，量子力学波函数对时间的演化是用么正算符。如果U(1)是把波函数演化一秒的算符，那么把波函数演化半秒的算符必须符合U(1)=U(1/2)U(1/2)。为了保证这样的算符存在（就像保证-1的平方根存在），量子力学的线性空间背后的域必须代数关闭。所以量子力学不能建立在实数上。
http://www.scottaaronson.com/democritus/lec9.html - 2012-02-03 04:17:39Derr12楼引用引用@Uroboros的回应：
因该是先有波函数的数学模型，后才有薛定谔方程的吧？整个方程本来就是建立在波函数的公设之上的。。。。假如一开始就把波函数弄成实值的，那么可能会导出另外一种类似薛定谔方程的方程（或者根本就导不出。。。）。。。话说，实值的时候也是可以干涉的，经典的波不就是这么干涉的吗？？。。。。。
经典的机械波或者光波其实也是具有相位的，仅仅是便于计算所以才单单提出实部进行演示。否则的话波的能量和振幅相关。如果仅用实数表示波函数，那么这个波就存在能量为零的时候，与现实观测不符。
恩...最后ls说的应该是幺正算符，既符合幺正变换的算符 - 2012-02-03 08:59:54Uroboros13楼引用引用@逻辑谬误 的回应：
http://www.scottaaronson.com/democritus/lec9.html
这种理解真独特啊。。。是个不错的课程！。。。我才开始学，所以有很多不太理解的地方，多谢你的指点与帮助！ - 2012-02-03 09:02:02Uroboros14楼引用引用@Derr的回应：
经典的机械波或者光波其实也是具有相位的，仅仅是便于计算所以才单单提出实部进行演示。否则的话波的能量和振幅相关。如果仅用实数表示波函数，那么这个波就存在能量为零的时候，与现实观测不符。
恩...最后ls说的应该是幺正算符，既符合幺正变换的算符
原来如此。。。看来我还要再去补补经典的波动理论。。。。 - 2012-02-03 10:59:13逻辑谬误15楼引用引用@Derr的回应：
经典的机械波或者光波其实也是具有相位的，仅仅是便于计算所以才单单提出实部进行演示。
我意见相反。古典波可以用单用三角函数去做。把实波复化是为了便于计算，但薛定谔方程式波是复波却无可避免的。
套进经典波方程式
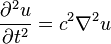，你会得到两条分别求f和g的独立方程式。
但薛定谔方程式对时间只做一级偏微分：，如果套入
，会得到实虚部相互依赖的方程式：
对古典波，因为实虚部独立，它等同于两条独立的实方程式。把波复化是为了便于计算。
但是对薛定谔方程式这样是不行的。所以它的解必须用复值函数。否则的话波的能量和振幅相关。
能量和振幅相关不是古典波的特征吗？如果仅用实数表示波函数，那么这个波就存在能量为零的时候，与现实观测不符。
只有在经典波才能有一瞬間波幅到处是0的解。薛定谔方程式因为它对时间只微分一次保证不会出现这样的非平凡解。 - 2012-02-03 11:59:42Uroboros16楼引用引用@逻辑谬误 的回应：
我意见相反。古典波可以用单用三角函数去做。把实波复化是为了便于计算，但薛定谔方程式波是复波却无可避免的。
套进经典波方程式，你会得到两条分别求f和g的独立方程式。
但薛定谔方程式对时间只做一级偏微分：，如果套入，会得到实虚部相互依赖的方程式：
对古典波，因为实虚部独立，它等同于两条独立的实方程式。把波复化是为了便于计算。
但是对薛定谔方程式这样是不行的。所以它的解必须用复值函数。
能量和振幅相关不是古典波的特征吗？
只有在经典波才能有一瞬間波幅到处是0的解。薛定谔方程式因为它对时间只微分一次保证不会出现这样的非平凡解。
大师啊！！！以后有不懂得就全指望你了！！！ - 2012-02-04 07:10:40Derr17楼引用引用@逻辑谬误 的回应：
我意见相反。古典波可以用单用三角函数去做。把实波复化是为了便于计算，但薛定谔方程式波是复波却无可避免的。
套进经典波方程式，你会得到两条分别求f和g的独立方程式。
但薛定谔方程式对时间只做一级偏微分：，如果套入，会得到实虚部相互依赖的方程式：
对古典波，因为实虚部独立，它等同于两条独立的实方程式。把波复化是为了便于计算。
但是对薛定谔方程式这样是不行的。所以它的解必须用复值函数。
能量和振幅相关不是古典波的特征吗？
只有在经典波才能有一瞬間波幅到处是0的解。薛定谔方程式因为它对时间只微分一次保证不会出现这样的非平凡解。
我说的就是经典波函数啊，而且为何我和你的观点就相反了？如果经典波函数能得到某时刻振幅为零，那么岂不是这时刻的能量为零了？所以说经典波函数的振幅其实并没有变化，变的是相位 - 2012-02-04 08:00:39Derr18楼引用引用@逻辑谬误 的回应：
我意见相反。古典波可以用单用三角函数去做。把实波复化是为了便于计算，但薛定谔方程式波是复波却无可避免的。
套进经典波方程式，你会得到两条分别求f和g的独立方程式。
但薛定谔方程式对时间只做一级偏微分：，如果套入，会得到实虚部相互依赖的方程式：
对古典波，因为实虚部独立，它等同于两条独立的实方程式。把波复化是为了便于计算。
但是对薛定谔方程式这样是不行的。所以它的解必须用复值函数。
关于你对经典波函数可以为实数薛定谔方程的解一定为复数我实在不能认同。
且不说对于波函数定态解，也就是函数时间偏导为零的解，里面就有符合薛定谔方程的实数解，
就算是对于随时间演化的波函数，按照你的等式，你是默认哈密顿算子只包含实数么？你让角动量算符情何以堪
另外就是对于经典波函数里面的实部和虚部，虽然单单代入方程里面看起来没有关联，但是复变函数本身的连续性就是要求他们满足拉普拉斯方程不是么？
所以我认为不管是量子力学还是经典波函数，在复数域上的解才能完全表示出波的物理学本质，而不是仅仅为了便于计算或者满足方程而附加的东西。 - 2012-02-04 09:13:42逻辑谬误19楼引用引用@Derr的回应：
关于你对经典波函数可以为实数薛定谔方程的解一定为复数我实在不能认同。
且不说对于波函数定态解，也就是函数时间偏导为零的解，里面就有符合薛定谔方程的实数解，
就算是对于随时间演化的波函数，按照你的等式，你是默认哈密顿算子只包含实数么？你让角动量算符情何以堪
对。因为哈密顿量是可观察物理量。所以某意义上它必须是实数。角动量算符也一样。也是可观察的物理量，两者只能有实特征值。情何以堪是什么意思？另外就是对于经典波函数里面的实部和虚部，虽然单单代入方程里面看起来没有关联，但是复变函数本身的连续性就是要求他们满足拉普拉斯方程不是么？
所以我认为不管是量子力学还是经典波函数，在复数域上的解才能完全表示出波的物理学本质，而不是仅仅为了便于计算或者满足方程而附加的东西。
复值函数和复变函数是两个不同的概念！复变函数的实虚部必须满足柯西－黎曼方程所以不是独立。但这又和波方程的解有什么关系？u(x,y,z,t)根本就不是C到C的映射。
另外，经典波完全可以在某时刻整个波幅完全为零。最典型的例子是驻波：琴弦波动有一瞬间整条弦是平的：看下图：
能量到哪里去？弦的振幅为0但振幅变化率却是最大！也就是所有能量都到动能去了。 - 2012-02-04 09:58:50逻辑谬误20楼引用引用@Derr的回应：
但是复变函数本身的连续性就是要求他们满足拉普拉斯方程不是么？
再对这点补充一下。你想讲的不是连续性，应该是全纯性（holomorphic）。全纯复变函数的实部和虚部不独立且分别满足拉普拉斯方程。这是必要条件，但不是充分條件。简单例子u(x,y)=x-iy 实虚部明显满足拉普拉斯方程但它不是全纯函数。 - 2012-02-04 20:05:33Derr21楼引用引用@逻辑谬误 的回应：
对。因为哈密顿量是可观察物理量。所以某意义上它必须是实数。角动量算符也一样。也是可观察的物理量，两者只能有实特征值。情何以堪是什么意思？
复值函数和复变函数是两个不同的概念！复变函数的实虚部必须满足柯西－黎曼方程所以不是独立。但这又和波方程的解有什么关系？u(x,y,z,t)根本就不是C到C的映射。
另外，经典波完全可以在某时刻整个波幅完全为零。最典型的例子是驻波：琴弦波动有一瞬间整条弦是平的：看下图：
能量到哪里去？弦的振幅为0但振幅变化率却是最大！也就是所有能量都到动能去了。
恩，复值复变什么的确实记不太清楚了，只是觉得波函数应该是在复数域上解析的。但是依旧不认同你的看法。
驻波不是存在某一时刻振幅为零的波，而是存在某一点振幅为零的波，驻波各个点的振幅的模并不会随时间改变，改变的只是相位而已。驻波可以分解为两个运动方向相反，振幅大小相同的波的叠加，用实数难以体现波势能动能变化，但是用复振幅就可以，所以说本质上通过复数表示波的相位更能体现其物理学本质。
最后，我说的是算子里面含有复数，不是说特征值为复数，你将方程拆成实部虚部两部分总应该考虑算子里面本身自带的实部虚部吧？ - 2012-02-04 23:19:06浔荆
22楼其实我本来是想说点什么的、、、看到上面的说的那么复杂，忽然没有信心了、、、引用
我记得之前看过一个波函数的推导过程，复数似乎是在三角函数向指数函数转化的那一步出现的 - 2012-02-05 06:48:42逻辑谬误23楼引用引用@Derr的回应：
恩，复值复变什么的确实记不太清楚了，只是觉得波函数应该是在复数域上解析的。但是依旧不认同你的看法。
波函数的变数是(t,x,y,z)是时间与位移。本身就不是活在复面上的函数。所以也就没有对复数域上解析的问题。当然你可以把t,x,y,z看作是复数的变数。那是另外一件可以讨论的事。驻波不是存在某一时刻振幅为零的波，而是存在某一点振幅为零的波，驻波各个点的振幅的模并不会随时间改变，改变的只是相位而已。驻波可以分解为两个运动方向相反，振幅大小相同的波的叠加，
驻波只是针对之前说”如果仅用实数表示波函数，那么这个波就存在能量为零的时候，与现实观测不符。”举反例，还可以举更广泛的例。不含阻尼项的古典波方程式的解，无论是实值或复值波都符合能量守恒。所以如果存在任何总能量为零的时候，那在所有时候总能量都必须为零。但很明显古典波方程式是有实值而能量不等于零的解。
（小补充：总能量值没有任何物理意义，所以零能量并不违反什么物理定律。我想你原本的“零能量”的意思是和没有任何波动的状态能量相等）
（再补充：用驻波只是想说明经典波方程允许在某时间到处都是0的解。有这性质的经典波解多得是。但有这性质的薛定谔方程式量子波解只有一个：所有时候、位置都等于0的平凡解）用实数难以体现波势能动能变化，但是用复振幅就可以，所以说本质上通过复数表示波的相位更能体现其物理学本质。
高中还没学复数之前不就用实值波：来解释波吗？只不过学了
发现可以用复数加法来处理原本很麻烦的三角函数加法而已。
古典波值在任何时候、位置都可以观察，所以就算不用虚数我们都必须可找到解（否则你怎么跟观察比较？）。数学用复数会不会比较简单看你三角函数好不好。相比一下，薛定谔方程的解是不能被直接观察的，所以不用一定是实数。
至于古典波的动能与势能。如果u(x,t)是个古典波（例如说均匀密度绳子的振幅好了），能量是：
第一项是动能，第二项是势能。无论u是实还是复值都很好分辨。最后，我说的是算子里面含有复数，不是说特征值为复数，你将方程拆成实部虚部两部分总应该考虑算子里面本身自带的实部虚部吧？
先说哈密顿量没有i出现，所以我原本的演示就没有问题。你说动量
有i怎么办？注意
是反自共轭算子，在用一意义上就像个虚数。乘i后p就是“实”了。你说这不对啊，对
，
，p好像就是个虚数了。但是
不是物理波函数，因为它不平方可积。
H和p这两个例子不是偶然。[b]所有相对物理观察的算子[/b]都是共轭算子、都具备这性质。 - 2012-02-05 06:50:55Derr24楼引用引用@逻辑谬误 的回应：
驻波只是针对之前说”如果仅用实数表示波函数，那么这个波就存在能量为零的时候，与现实观测不符。“举反例，我可以举更广泛的例。不含阻尼项的古典波方程式的解，实值或复值，都符合能量守恒。所以如果存在总能量为零的时候，那它在所有时候总能量都必须为零。但很明显古典波方程式是有实值而能量不等于零的解。
不是太明白你是如何反驳的，你的反例不能证明“仅用实数表示波函数就不存在能量为零”，你只是说“波确实不存在能量为零的时刻”。不是太明白你是如何通过实数波函数求出波的势能的。
高中还没学复数之前不就用实值波：来解释波吗？只不过学了发现可以用复数加法来处理原本很麻烦的三角函数加法而已。
古典波值在任何时候、位置都可以观察，所以就算不用虚数我们都可以找到解（否则你怎么跟观察比较？）。数学用复数会不会比较简单看你三角函数好不好。相比一下，薛定谔方程的解是不能被直接观察的，所以不用一定是实数。
至于古典波的动能与势能。如果u(x,t)是个古典波（例如说均匀密度绳子的振幅好了），请写下它的总能量公式。你会发现动能与势能项很明显的分开。这点用不用复数來处理u都一样。
在没学习复数之前我还能用实数表示势阱里面电子波函数呢，这并不能说明经典波函数不需要引入复数。我没有看出引入复数之后计算哪里有简化，本质上用到的依旧是三角函数那些知识。
确实你可以将波的能量拆分成动能和势能两部分，就像你可以把哈密顿量拆成动能和势能两部分一样，但是你觉得势能部分可以从波动方程里面求出来么？
先说哈密顿量没有i出现，所以我原本的演示就没有问题。你说动量有i怎么办？注意是反自共轭算子，在用一意义上就算嘅纯虚数。乘i后p就是“实”了。你说这不对啊，是p的特征函数，特征值-ik是虚的。但它不能是物理波函数因为它不是平方可积。
举这两个例子不是偶然，是所有和物理观察相应的算子都是共轭算子、都具备这性质。
其实我不想谈这方面的，毕竟已经达成一致，争吵显得很没有意义。但是还是需要注意你证明的时候把波函数拆成实部和虚部两个部分了，虽然这么做在数学上可行，但是并没有太大物理意义，而且证明过程是存在问题的。
最后，你的哈密顿量形式貌似不对，我估计你是用了自然单位制并且假定了这个是在势场中的电子波函数的哈密顿量，所以约化了质量和普朗克常量。但是你的哈密顿量里面依旧多了一个普朗克常数出来 - 2012-02-05 07:09:55逻辑谬误25楼引用引用@Derr的回应：
不是太明白你是如何反驳的，你的反例不能证明“仅用实数表示波函数就不存在能量为零”，你只是说“波确实不存在能量为零的时刻”。不是太明白你是如何通过实数波函数求出波的势能的。
我说的是实值的经典波。楼上那里积分第二项就是一根波动绳子拉力造成的势能、第一项是动能。
我反证有两段。
第一”如果仅用实数表示波函数，那么这个波就存在能量为零的时候“。找一个实波（例如u(x,t)=sin(x-ct)），它在任何时候能量相等（能量守恒）。所以只要你不透过取适地取势能的0点，而把t=0的能量设成0，这个波的能量就[b]任何时间[/b]都不为0。
第二”能量为零与现实观测不符“。能量=0本身并不违反任何物理原理。看你势能的0点设在哪里。
（注意：当我导论经典波，我从来不用”波函数“这字眼，把它留给量子波。）在没学习复数之前我还能用实数表示势阱里面电子波函数呢，这并不能说明经典波函数不需要引入复数。我没有看出引入复数之后计算哪里有简化，本质上用到的依旧是三角函数那些知识。
确实你可以将波的能量拆分成动能和势能两部分，就像你可以把哈密顿量拆成动能和势能两部分一样，但是你觉得势能部分可以从波动方程里面求出来么？
你解的是定态。也就是与时无关薛定谔方程的解。那个可以是实数，我不反对。如你所说，势阱电子波函数可以都是实的。
但我们讨论的是与时向关薛定谔方程的解。只要你加入时间部，复数就无可避免。也就是说，薛定谔方程的解在某一时刻可以完全是实的，但不能在所有时间都是实的。其实我不想谈这方面的，毕竟已经达成一致，争吵显得很没有意义。但是还是需要注意你证明的时候把波函数拆成实部和虚部两个部分了，虽然这么做在数学上可行，但是并没有太大物理意义，而且证明过程是存在问题的。
最后，你的哈密顿量形式貌似不对，我估计你是用了自然单位制并且假定了这个是在势场中的电子波函数的哈密顿量，所以约化了质量和普朗克常量。但是你的哈密顿量里面依旧多了一个普朗克常数出来
单位方面我是偷懒。 - 2012-02-05 07:17:35逻辑谬误26楼引用其实我不想谈这方面的，毕竟已经达成一致，争吵显得很没有意义。
我喜欢参与这种讨论因为同样的问题通常都是我教量子力学时学生会提出的问题。有时侯自己觉得很明显的命题却理解不了学生疑惑的出发点。但看过各种网上出现的误解后，就开始累积应该从哪方向教导的经验。 - 2012-02-05 10:19:10Derr27楼老师么...压力很大，想起那个让我欲仙欲死的量子力学老师...引用
不过我还是认为我的观点是对的引用@逻辑谬误 的回应：
第一”如果仅用实数表示波函数，那么这个波就存在能量为零的时候“。找一个实波（例如u(x,t)=sin(x-ct)），它在任何时候能量相等（能量守恒）。所以只要你不透过取适地取势能的0点，而把t=0的能量设成0，这个波的能量就[b]任何时间[/b]都不为0。
第二”能量为零与现实观测不符“。能量=0本身并不违反任何物理原理。看你势能的0点设在哪里。
（注意：当我导论经典波，我从来不用”波函数“这字眼，把它留给量子波。）
我也觉得不用波函数比较好，有时候感觉很别扭
其实我想说的是我认为“存在一列波，其计算出来某一时刻能量为零”，也就是说单单是举反例是不能反驳我的观点的。
比如说有一列波f(t)=Asin(ax-wt)，那么就存在某一时刻f(t0)=0，这时候如果是振幅的平方，那么计算出来他的能量为零，或者说他的能量（事实上只是动能）是变化的。但是如果我们用一个传感器来测量，这列波的能量应该是一个恒定值。所以说经典波里面复数表示也是必要的
事实上就算是通过求解波动方程，你一样可以得到带有相位的通解，实数解只是其中一个特解罢了 - 2012-02-05 12:22:15逻辑谬误28楼引用引用@Derr的回应：
其实我想说的是我认为“存在一列波，其计算出来某一时刻能量为零”，也就是说单单是举反例是不能反驳我的观点的。
比如说有一列波f(t)=Asin(ax-wt)，那么就存在某一时刻f(t0)=0，这时候如果是振幅的平方，那么计算出来他的能量为零，或者说他的能量（事实上只是动能）是变化的。
先重申以下讨论的是经典波。例如讨论一根绳子的波动好了。
给任意波解f(x,t)：（单位设定波速=1)，那很容易发现g(x,t)=f(x,t)-f(x,-t)也是一个波解，而且g(x,0)=0。所以这就满足在某时间波幅为0这條件了。从你的例子出发得到g(x,t)=A sin(kx-wt)-Asin(kx+wt)。你可以自己测g(x,0)=0。
但它能量不为0，动能更不为0。因为它在那瞬间对时间偏微分不为0：对绳子这例子。波幅对时间的微分（的一半）正是它的动能密度。
动能密度：
势能密度：
所以在波幅为0那一刻，动能不是0而是势能！也就是所有能量都是动能，在那一刻像一个到达最低点的摆：动能达到最大值！
总能量当然在任何时间都一样。能量守恒是诺特定理的简单结果。但是如果我们用一个传感器来测量，这列波的能量应该是一个恒定值。所以说经典波里面复数表示也是必要的
事实上就算是通过求解波动方程，你一样可以得到带有相位的通解，实数解只是其中一个特解罢了
为什么能量守恒就一定要复数波？任何仪器都不能测量复数值的东西。任何可以测量的数值都必须是实数。 - 2012-02-05 13:47:15Uroboros29楼引用引用@Derr的回应：老师么...压力很大，想起那个让我欲仙欲死的量子力学老师...
不过我还是认为我的观点是对的
我也觉得不用波函数比较好，有时候感觉很别扭
其实我想说的是我认为“存在一列波，其计算出来某一时刻能量为零”，也就是说单单是举反例是不能反驳我的观点的。
比如说有一列波f(t)=Asin(ax-wt)，那么就存在某一时刻f(t0)=0，这时候如果是振幅的平方，那么计算出来他的能量为零，或者说他的能量（事实上只是动能）是变化的。但是如果我们用一个传感器来测量，这列波的能量应该是一个恒定值。所以说经典波里面复数表示也是必要的
事实上就算是通过求解波动方程，你一样可以得到带有相位的通解，实数解只是其中一个特解罢了
@逻辑谬误@Derr
看了你们这么多的讨论，关于经典波的能量的观点我认为@逻辑谬误 是对的。@Derr你对振幅的理解好像有误。。。在无阻尼振动时，振幅是一个常数项，并不是说f(t0)=0了振幅就是0.也许你理解的振幅就是单纯意义上“波在某一时刻振动的幅度”？？。。。但是这么理解显然是不对的。。。
@逻辑谬误 你给的资料我好好看了一下，大概明白为什么波函数要取复值的含义了，我说一下，你看我理解的对不对：波函数其实是用来描述某个存在之存在的概率的函数，但是量子力学最基本的公设，包括双缝实验的结果，认为存在本身是可以相互干涉的。。。也就是说，这个时候发生干涉的不是物质和物质之间的干涉，而是某个存在自身的存在性与存在性之间的干涉！由于这种干涉的存在，如果波函数仍然直接仅仅使用经典意义下的概率（0<=P<=1）来描述一个存在的存在性，那么它将无法实现对自身存在性的干涉，即无法解释双缝实验的结果。。。。因此，取复数是由于量子概率波本身的特性决定的，为了处理这种情况，相当于要重新定义（或者推广）数学中的概率，由原来1-范数的定义方式推广到了2-范数的定义方式，从而允许在获得一个存在的存在概率之前首先完成其自身存在性之间的叠加，这样做的结果才符合实验观测。。。 - 2012-02-05 15:13:42逻辑谬误30楼引用引用@Uroboros的回应：
@逻辑谬误 你给的资料我好好看了一下，大概明白为什么波函数要取复值的含义了，我说一下，你看我理解的对不对：波函数其实是用来描述某个存在之存在的概率的函数，但是量子力学最基本的公设，包括双缝实验的结果，认为存在本身是可以相互干涉的。。。也就是说，这个时候发生干涉的不是物质和物质之间的干涉，而是某个存在自身的存在性与存在性之间的干涉！由于这种干涉的存在，如果波函数仍然直接仅仅使用经典意义下的概率（0<=P<=1）来描述一个存在的存在性，那么它将无法实现对自身存在性的干涉，即无法解释双缝实验的结果。。。。因此，取复数是由于量子概率波本身的特性决定的，为了处理这种情况，相当于要重新定义（或者推广）数学中的概率，由原来1-范数的定义方式推广到了2-范数的定义方式，从而允许在获得一个存在的存在概率之前首先完成其自身存在性之间的叠加，这样做的结果才符合实验观测。。。
这里面好多句“存在”我看不太懂了。从来不把量子力学想到那么禅。
我不知道你能不能单单从量子波函数是复数这点看出波函数值和概率有关这物理理解。你最多只能说，因为波函数值不局限于实数，所以波函数值本身不可能是可以被观察到的量（古典波的波值在任何时间、位置都是可观察的物理量）。它的幕平方是实数，把其理解成概率分布在我看来只是有充分实验证据支持的量子力学公设而沒什么“非这样不可”的哲学理由。
至於干涉、双缝实验，电子的总波函数是它分别单穿过一个洞的波函数的叠加。这基本上是叠加原理的一种表现。把它理解成是自己和自己干涉可以帮助你理解的话也可以。实验上我们也可以保证每次只有一粒电子越过双缝，所以它也只有自己能干涉。不过，我的建议学习期间不要太过执着于把量子现象“合理化”而卡住。生活在经典环境的我们缺乏完美描述量子现象的字眼和直觉。哥本哈根解释虽然是大部分物理学家所接受的解释，但不少研究人员还不满于它的概率和波函数倒塌等细节而做前端研究。 - 2012-02-05 17:43:45Uroboros31楼引用引用@逻辑谬误 的回应：
不过，我的建议学习期间不要太过执着于把量子现象“合理化”而卡住。生活在经典环境的我们缺乏完美描述量子现象的字眼和直觉。哥本哈根解释虽然是大部分物理学家所接受的解释，但不少研究人员还不满于它的概率和波函数倒塌等细节而做前端研究。
这点我也明白，但是不搞清楚时心中总有一个结，每当想到这里的时候就特别纠结。。。其实理解到公设那个层面就已经够了，进一步去思考或试图解释这些公设怎么来的就会不可避免的遇到各种无法理解的地方。。。。虽然知道这些不是自己应该思考的，但是就如同强迫症一般想要弄明白。。。结果就像你说的“太过执着于把量子现象“合理化”而卡住”。。。 - 2012-02-05 19:23:46Derr32楼引用引用@逻辑谬误 的回应：
先重申以下讨论的是经典波。例如讨论一根绳子的波动好了。
给任意波解f(x,t)：（单位设定波速=1)，那很容易发现g(x,t)=f(x,t)-f(x,-t)也是一个波解，而且g(x,0)=0。所以这就满足在某时间波幅为0这條件了。从你的例子出发得到g(x,t)=A sin(kx-wt)-Asin(kx+wt)。你可以自己测g(x,0)=0。
但它能量不为0，动能更不为0。因为它在那瞬间对时间偏微分不为0：对绳子这例子。波幅对时间的微分（的一半）正是它的动能密度。
动能密度：
势能密度：
所以在波幅为0那一刻，动能不是0而是势能！也就是所有能量都是动能，在那一刻像一个到达最低点的摆：动能达到最大值！
总能量当然在任何时间都一样。能量守恒是诺特定理的简单结果。
为什么能量守恒就一定要复数波？任何仪器都不能测量复数值的东西。任何可以测量的数值都必须是实数。
好吧，我确实没什么理由反驳了，只是觉得既然波动方程解出来是一个复值那么这个虚部必然有他存在的意义。
另外确实仪器测不出来虚数，但是复数的模平方是可以测出来的，对应波函数里面的概率密度...好吧我不知道概率密度可不可测 - 2012-02-05 19:31:42Derr33楼引用引用@Uroboros的回应：
这点我也明白，但是不搞清楚时心中总有一个结，每当想到这里的时候就特别纠结。。。其实理解到公设那个层面就已经够了，进一步去思考或试图解释这些公设怎么来的就会不可避免的遇到各种无法理解的地方。。。。虽然知道这些不是自己应该思考的，但是就如同强迫症一般想要弄明白。。。结果就像你说的“太过执着于把量子现象“合理化”而卡住”。。。
双引号里面要用单引号引用。
其实把某个现象“合理化”的想法应该是很正常的吧，总要找个理由说服自己相信这个公设，特别是这个公设并不是这么显而易见的时候。本质上现存的物理学定理都是一些猜想，我相信在这些猜想背后肯定有更深刻的规律在里面。
对这种情况最好的办法就是多去应用这个公设，用多了自然就会相信，就像高中时候不停用能量守恒做题，所以人人都相信这个世界是能量守恒的了。 - 2012-02-06 00:44:12Uroboros34楼引用引用@Derr的回应：
双引号里面要用单引号引用。
其实把某个现象“合理化”的想法应该是很正常的吧，总要找个理由说服自己相信这个公设，特别是这个公设并不是这么显而易见的时候。本质上现存的物理学定理都是一些猜想，我相信在这些猜想背后肯定有更深刻的规律在里面。
对这种情况最好的办法就是多去应用这个公设，用多了自然就会相信，就像高中时候不停用能量守恒做题，所以人人都相信这个世界是能量守恒的了。
感觉有点像“龙寓”了：
“仓库的墙为什么是黑的？“
”嘘，那是因为有一条龙在里面。。。“
“我能看见那条龙吗？”
”当然不能，不论你用什么方法你都看不到它的！”
“那墙为什么一定是龙弄黑的呢？”
“这是‘公设’！这符合实际实验观察和理论推导。。。”
“我觉得这个‘公设’很别扭。。。它不符合我们日常的生活经验，有点。。。不合理。。。”
“没关系，对这种情况最好的办法就是多去应用这个公设，用多了自然就会相信，就像高中时候不停用能量守恒做题，所以人人都相信这个世界是能量守恒的了。”
“。。。。。。。。。。。。。。。。。。。。。。。。。” - 2012-02-06 01:13:48Derr35楼引用引用@Uroboros的回应：
。。。。。。。。。。。。。。。。。。。。。。。。。”
其实从一开始人们选择的理论就不一定是对的，任何两套符合观测的理论你都无法区分他们的对错。
比如说地心说和日心说，其实你是不能“推翻”地心说的，他完全可以附加更多的“定律”来使得地心说符合天文观测，比如当时为了解释太阳系各大行星诡异的运行轨道，人们提出“本轮”“均轮”的理论，将行星轨道细分成为很多小的圆形轨道，圆形轨道上再套更小的圆形轨道
就像现在人们认为波函数是很多特征波函数的线性叠加一样...
但是为什么人们要抛弃地心说而选择日心说？因为他是“最简单的”理论，能直观方便地解释各种现象并推导出更多有用的规律（比如万有引力）。就像你能用无限复杂的理论认为龙的存在，也可以用简单的“公设”认为龙不存在
这其实有点像声明演化一样，适者生存，人们相信一个“错”的观点随着各种新现象的发现，其为了保证自己的正确性而需要提出的理论复杂度将会无限增大，最终被人抛弃。
这其实也是为什么大部分物理学家更愿意相信“美”的理论而不一定是“符合事实观测”的理论的原因。 - 2012-02-07 18:17:59talentedpope
36楼我有个老师曾经和我说，“不知道为什么，用复数来描述这自然界的大部分事物会很自然（然后他举了若干我听不懂的例子），所以有很多数学家觉得复数才是最自然的数而非数学家造出来的数学玩具。”。。引用 - 2012-02-07 18:29:43Uroboros37楼引用引用@talented pope 的回应：我有个老师曾经和我说，“不知道为什么，用复数来描述这自然界的大部分事物会很自然（然后他举了若干我听不懂的例子），所以有很多数学家觉得复数才是最自然的数而非数学家造出来的数学玩具。”。。
这里用复数，主要是为了得到“负概率”。。。举个例子（可能不恰当。。。）：某天晚上，如果你在家吃饭的概率是正的，那么你出去吃饭的概率就是负的。。。为了依然保证归一化（即所有概率相加取绝对值等于1），出去吃饭的概率的绝对值越大，在家吃饭概率的绝对值就越小（假设只有这两种情况）。。。。无论如何都要保证相加以后的绝对值为1。。。。这就是我对“负概率”的理解。。。。量子力学中至因为要用这种“负概率”，就是为了使得概率波函数得以产生叠加。。。（你可以想想，如果和日常生活中一样，概率都取0到1的实数，波函数如何叠加？？。。。。） - 2012-02-07 20:18:30逻辑谬误38楼引用引用@talented pope 的回应：我有个老师曾经和我说，“不知道为什么，用复数来描述这自然界的大部分事物会很自然（然后他举了若干我听不懂的例子），所以有很多数学家觉得复数才是最自然的数而非数学家造出来的数学玩具。”。。
因为复数代数上关闭系统。复数是实数的闭合代数扩张。
http://zh.wikipedia.org/wiki/%E4%BB%A3%E6%95%B8%E6%93%B4%E5%BC%B5
基本上是这样：实数的多项式不一定有实数解（x^2+1=0），但复数多项式保证有复数解。
别忘了还有四元数和八元数这些更广泛化的“数”。麦克斯韦本人是用四元数写下他的方程组的！但当时（今天也是）物理学家沒什么人会四元数，所以一直下来我们都用向量微分。 - 2012-02-07 20:23:04逻辑谬误39楼引用引用@Uroboros的回应：
这里用复数，主要是为了得到“负概率”。。。举个例子（可能不恰当。。。）：某天晚上，如果你在家吃饭的概率是正的，那么你出去吃饭的概率就是负的。。。为了依然保证归一化（即所有概率相加取绝对值等于1），出去吃饭的概率的绝对值越大，在家吃饭概率的绝对值就越小（假设只有这两种情况）。。。。无论如何都要保证相加以后的绝对值为1。。。。这就是我对“负概率”的理解。。。。量子力学中至因为要用这种“负概率”，就是为了使得概率波函数得以产生叠加。。。（你可以想想，如果和日常生活中一样，概率都取0到1的实数，波函数如何叠加？？。。。。）
字眼要小心。古典还是量子概率只能是[0,1]。波函数的值我们叫做概率幅（Probability Amplitude）。概率幅是一个复数。
与其说它可以是负数，我喜欢想象概率幅为一个箭头。然后干涉就是把箭头头接尾地连起来，最后取和原点的距离（平方）就得概率。 - 2012-02-07 20:57:16Uroboros40楼引用引用@逻辑谬误 的回应：
字眼要小心。古典还是量子概率只能是[0,1]。波函数的值我们叫做概率幅（Probability Amplitude）。概率幅是一个复数。
额。。。最近有点混乱。。。因为我想虚数平方以后可能会是负数。。。但如果是取模的话，那一定就是正的了。。。 - 2012-02-08 01:53:26逻辑谬误41楼引用引用@Uroboros的回应：
额。。。最近有点混乱。。。因为我想虚数平方以后可能会是负数。。。但如果是取模的话，那一定就是正的了。。。
不是平方。是幕平方。概率只能介乎0和1之间。 - 2012-02-08 04:17:32Derr42楼引用引用@Uroboros的回应：
额。。。最近有点混乱。。。因为我想虚数平方以后可能会是负数。。。但如果是取模的话，那一定就是正的了。。。
不是平方，而是模平方，也就是乘上他的复共轭
而且波函数振幅模平方之后也不是概率，而是概率密度（Probability density）对一个空间求积分之后才是“粒子在这个空间内被观测到的概率” - 2012-02-08 12:45:40Uroboros43楼@逻辑谬误 ：引用
有个问题想请教你。。。为了引入一维量子谐振子问题，书上说把一维势场函数V(x)泰勒展开到平方项，然后取V(0)=0,由于x=0时处于平衡位置，因此此时V'(0)=0。这样就只剩下二次项，即V(x)≈(1/2)V'(0)x^2。。。。到这里都好理解。。。但是，突然书上就直接给出了这个表达式：V(x)=(1/2)mωx^2...这里就看不明白了，势场函数V(x)的表达式前面都没有给出，为什么这里可以得到这个具体的表达式？还有，这个突然出现的ω是什么？？。。。。。
P.S.话说我是不是应该换一本书呢。。。。。。 - 2012-02-08 15:51:18逻辑谬误44楼引用引用@Uroboros的回应：@逻辑谬误 ：
有个问题想请教你。。。为了引入一维量子谐振子问题，书上说把一维势场函数V(x)泰勒展开到平方项，然后取V(0)=0,由于x=0时处于平衡位置，因此此时V'(0)=0。这样就只剩下二次项，即V(x)≈(1/2)V'(0)x^2。。。。到这里都好理解。。。但是，突然书上就直接给出了这个表达式：V(x)=(1/2)mωx^2...这里就看不明白了，势场函数V(x)的表达式前面都没有给出，为什么这里可以得到这个具体的表达式？还有，这个突然出现的ω是什么？？。。。。。
P.S.话说我是不是应该换一本书呢。。。。。。
你要不要开个新贴来讨论啊。
先温习一下古典力學的谐振子。原理是一样的。
如果弹簧常数是k，它的势能就是1/2kx^2。所以V''(0)也就是有效弹簧常数。而弹簧的自然频率是：k/m = w^2。公式完全一样。 - 2012-02-08 17:19:39Uroboros45楼引用引用@逻辑谬误 的回应：
你要不要开个新贴来讨论啊。
先温习一下古典力學的谐振子。原理是一样的。
如果弹簧常数是k，它的势能就是1/2kx^2。所以V''(0)也就是有效弹簧常数。而弹簧的自然频率是：k/m = w^2。公式完全一样。
谢谢，不用新开了。。。我只是感觉这个V"(0)来的蹊跷。。。。连V(x)都不知道，怎么就突然得到V"(0)的值了？。。。。
本帖来自
死理性派小组
95716人加入他们推荐了本文
同小组最新帖子
（全部）逛了这么久的果壳，最后定为在这个小组发展吧！提问你是神马主义者
0发表：沿途有弦为什么有的人财富积累那么快，请死理性派来分析一下
7发表：粉乎乎别说这些符号你都知道怎么读
8发表：环行使者有时候真觉得中国民智永远开启不了
52发表：金馆长之笑很有趣的数学悖论，求一针见血
230发表：の1im2《这个男人来自地球》的一点小破绽
3发表：呆乐平
No comments:
Post a Comment