主要的维度 A 本身含有的“能量”(即该维度的方差),受到这些个相关维度的干扰，它的能量被削弱了,通过PCA处理后，使维度A与其他维度的相关性 尽可能减弱，进而恢复维度A应有的能量，让我们“听的更清楚”！

偏最小二乘回归

1. 问题

这节我们请出最后的有关成分分析和回归的神器PLSR。PLSR感觉已经把成分分析和回归发挥到极致了，下面主要介绍其思想而非完整的教程。让我们回顾一 下最早的Linear Regression的缺点：如果样例数m相比特征数n少（m<n）或者特征间线性相关时，由于（n*n矩阵）的秩小于特征个数（即不可逆）。因此最小二乘法就会失效。
为了解决这个问题，我们会使用PCA对样本X（m*n矩阵）进行降维，不妨称降维后的X为X’（m*r矩阵，一般加了’就表示转置，这里临时改变下），那么X’的秩为r（列不相关）。

2. PCA Revisited

所谓磨刀不误砍柴工，这里先回顾下PCA。
令X表示样本，含有m个样例，每个样例特征维度为n，。假设我们已经做了每个特征均值为0处理。
如果X的秩小于n，那么X的协方差矩阵的秩小于n，因此直接使用线性回归的话不能使用最小二乘法来求解出唯一的，我们想使用PCA来使得可逆，这样就可以用最小二乘法来进行回归了，这样的回归称为主元回归（PCR）。
PCA的一种表示形式：


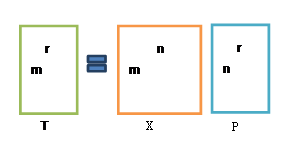
其中X是样本矩阵，P是X的协方差矩阵的特征向量（当然是按照特征值排序后选取的前r个特征向量），T是X在由P形成的新的正交子空间上的投影（也是样本X降维后的新矩阵）。
在线性代数里面我们知道，实对称阵A一定存在正交阵P，使得为对角阵。因此可以让的特征向量矩阵P是正交的。
其实T的列向量也是正交的，不太严谨的证明如下：

其中利用了，这是求P的过程，是对角阵，对角线上元素就是特征值。这里对P做了单位化，即。这就说明了T也是正交的， P是的特征向量矩阵，更进一步，T是的特征向量矩阵（。
这样经过PCA以后，我们新的样本矩阵T（m*r）是满秩的，而且列向量正交，因此直接代入最小二乘法公式，就能得到回归系数。

PCA的另一种表示：
（假设X秩为n）
这个公式其实和上面的表示方式没什么区别。
（当然我们认为P是n*n的，因此）
如果P是n*r的，也就是舍弃了特征值较小的特征向量，那么上面的加法式子就变成了

这里的E是残差矩阵。其实这个式子有着很强的几何意义，是第大特征值对应的归一化后的特征向量，就是X在上的投影。就是X先投影到上，还以原始坐标系得到的X’。下面这个图可以帮助理解：

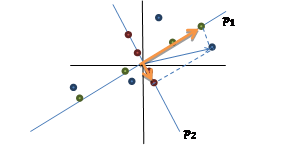
黑色线条表示原始坐标系，蓝色的点是原始的4个2维的样本点，做完PCA后，得到两个正交的特征向量坐标和。绿色点是样本点在上的投影（具有最大方差），红色点是在上的投影。的每个分量是绿色点在上的截距，是红色点在上的截距。中的每个分量都可以看做是方向为，截距为相应分量大小的向量，如那个上的橘色箭头。就得到了X在的所有投影向量，由于和正交，因此就相当于每个点的橘色箭头的加和，可想而知，得到了原始样本点。
如果舍弃了一些特征向量如，那么通过只能还原出原始点的部分信息（得到的绿色点，丢失了蓝色点在另一维度上的信息）。另外，P有个名字叫做loading矩阵，T叫做score矩阵。

3. PLSR思想及步骤

我们还需要回味一下CCA来引出PLSR。在CCA中，我们将X和Y分别投影到直线得到u和v，然后计算u和v的Pearson系数（也就是Corr(u,v)），认为相关度越大越好。形式化表示：

Maximize Subject to:

其中a和b就是要求的投影方向。
想想CCA的缺点：对特征的处理方式比较粗糙，用的是线性回归来表示u和x的关系，u也是x在某条线上的投影，因此会存在线性回归的一些缺点。我们想把 PCA的成分提取技术引入CCA，使得u和v尽可能携带样本的最主要信息。还有一个更重要的问题，CCA是寻找X和Y投影后u和v的关系，显然不能通过该 关系来还原出X和Y，也就是找不到X到Y的直接映射。这也是使用CCA预测时大多配上KNN的原因。
而PLSR更加聪明，同时兼顾PCA和CCA，并且解决了X和Y的映射问题。看PCA Revisited的那张图，假设对于CCA，X的投影直线是，那么CCA只考虑了X的绿色点与Y在某条直线上投影结果的相关性，丢弃了X和Y在其他维度上的信息，因此不存在X和Y的映射。而PLSR会在CCA的基础上再做一步，由于原始蓝色点可以认为是绿色点和红色点的叠加，因此先使用X的绿色点对Y做回归（，样子有点怪，两边都乘以就明白了，这里的Y类似于线性回归里的，类似），然后用X的红色点对Y的剩余部分F做回归（得到，）。这样Y就是两部分回归的叠加。当新来一个x时，投影一下得到其绿色点和红色点，然后通过r就可以还原出Y，实现了X到Y的映射。当然这只是几何上的思想描述，跟下面的细节有些出入。
下面正式介绍PLSR：
1） 设X和Y都已经过标准化（包括减均值、除标准差等）。
2） 设X的第一个主成分为，Y的第一个主成分为，两者都经过了单位化。（这里的主成分并不是通过PCA得出的主成分）
3） ，，这一步看起来和CCA是一样的，但是这里的p和q都有主成分的性质，因此有下面4）和5）的期望条件。
4） ，即在主成分上的投影，我们期望是方差最大化。
5） ，这个跟CCA的思路一致。
6） 综合4）和5），得到优化目标。
形式化一点：

Maximize Subject to:

看起来比CCA还要简单一些，其实不然，CCA做完一次优化问题就完了。但这里的和对PLSR来说只是一个主成分，还有其他成分呢，那些信息也要计算的。
先看该优化问题的求解吧：
引入拉格朗日乘子

分别对求偏导，得


从上面可以看出（两边都乘以p或q，再利用=1的约束）
下式代入上式得到

上式代入下式得到

目标函数，要求最大。
因此就是对称阵的最大特征值对应的单位特征向量，就是最大特征值对应的单位特征向量。
可见和是投影方差最大和两者相关性最大上的权衡，而CCA只是相关性上最大化。
求得了和，即可得到


这里得到的和类似于上图中的绿色点，只是在绿色点上找到了X和Y的关系。如果就此结束，会出现与CCA一样的不能由X到Y映射的问题。
利用我们在PCA Revisited里面的第二种表达形式，我们可以继续做下去，建立回归方程：


这里的c和d不同于p和q，但是它们之间有一定联系，待会证明。E和G是残差矩阵。
我们进行PLSR的下面几个步骤：
1） ，使用对Y进行回归，原因已经解释过，先利用X的主成分对Y进行回归。
2） 使用最小二乘法，计算c，d，r分别为：



实际上这一步计算出了各个投影向量。
和的关系如下：

再谈谈和的关系，虽然这里将替换成可以满足等式要求和几何要求，而且就是X投影出的方向向量。但这里我们想做的是回归（让E尽可能小），因此根据最小二乘法得到的一般与不同。
3） 将剩余的E当做新的X，剩余的F当做新的Y，然后按照前面的步骤求出和，得到：


目标函数，这个与前面一样，和分别是新的和的最大特征值对应的单位特征向量。
4） 计算得到第二组回归系数：


这里的和之前的是正交的，证明如下：

其实和不同的都是相互正交的。
同样和不同的也是正交的。


但和不同的一般不是正交的。
5） 从上一步得到回归方程：


如果还有残差矩阵的话，可以继续计算下去。
6） 如此计算下去，最终得到：


与PCA中表达式不一样的是这里的和不同的之间一般不是正交的。
其实这里不必一直计算到n，可以采用类似于PCA的截尾技术，计算到合适的r即可。关于r数目的选取可以使用交叉验证方法，这与PCA里面的问题类似。
另外，和的关系是
上面的公式如果写成矩阵形式如下：


这就是的回归方程，其中。
在计算过程中，收集一下P和R的值即可。
7） 使用PLSR来预测。
从6）中可以发现Y其实是多个回归的叠加（其实已经回归出Y的最主要信息）。我们在计算模型的过程中，得到了p和r。那么新来一个x，首先计算u（这里的u变成了实数，而不是向量了），得到
, , …
然后代入Y的式子即可求出预测的y向量，或者直接代入
8） 至此，PLSR的主要步骤结束。

4. PLSR相关问题

1） 其实不需要计算v和q，因为我们使用u去做Y的回归时认为了，其中c是常数。之所以这样是因为前面提到过的Y可以首先在X的主要成分上做回归，然后将Y的残差矩阵在X的残差矩阵的主要成分上做回归。最后X的各个成分回归之和就是Y。
2） 一般使用的PLSR求解方法是迭代化的求解方法，称之为NIPALS，还有简化方法SIMPLS，这些方法在一般论文或参考文献中提供的网址里都有，这里就不再贴了。
3） PLSR里面还有很多高级话题，比如非线性的Kernel PLSR，异常值检测，带有缺失值的处理方法，参数选择，数据转换，扩展的层次化模型等等。可以参考更多的论文有针对性的研究。还有PLSR的几个例子在参考文件里面有，不过都不详细。

5. 一些感悟

本文试图将PCA、CCA、PLSR综合起来对比、概述和讨论，不免对符号的使用稍微都点混乱，思路也有穿插混淆。还是以推导出的公式为主进行理解吧，另外文中个人理解的内容难免有错，望不吝赐教。
之前也陆陆续续地关注了一些概率图模型和时间序列分析，以后可能会转向介绍这两方面的内容，也会穿插一些其他的内容。说实话，自学挺吃力的，尤其对我这样 一个不是专业搞ML的人来说，也需要花大量时间。感叹国外的资料多，lecture多，视频多，可惜因为我这的网速和GFW原因，看不了教学视频，真是遗 憾。

6. 参考文献：

1. PARTIAL LEAST-SQUARES REGRESSION: A TUTORIAL. Paul Geladi and Bruce R. Kowalski
2. 王惠文－偏最小二乘回归方法及应用
3. Partial Least Squares (PLS) Regression.
4. A Beginner’s Guide to Partial Least Squares Analysis
5. Nonlinear Partial Least Squares: An Overview
6. http://www.statsoft.com/textbook/partial-least-squares/
7. Canonical Correlation a Tutorial
8. Pattern Recognition And Machine Learning
此文转载jerrylead

十二月 21st, 2011

No comments yet

admin

我理解的特征值与特征向量

1．如何理解矩阵，特征值和特征向量？
答：线性空间中，当你选定一组基之后，不仅可以用一个向量来描述空间中的任何一个对象，而且可以用矩阵来描述该空间中的任何一个运动（变换），从而得出矩阵是线性空间里的变换的描述。而使某个对象发生对应运动（变换）的方法，就是用代表那个运动（变换）的矩阵，乘以代表那个对象的向量。转换为数学语言： 是矩阵， 是向量， 相当于将 作线性变换从而得到 ，从而使得矩阵 （由n个向量组成）在对象或者说向量 上的变换就由简单的实数 来刻画，由此称 为矩阵A的特征值，而 称为 对应的特征向量。
总结来说，特征值和特征向量的出现实际上将复杂的矩阵由实数和低维的向量来形象的描述（代表），实现了降维的目的。在几何空间上还可以这样理解：矩阵A是向量的集合，而 则是向量的方向， 可以理解为矩阵A在 方向上作投影，而矩阵又是线性空间变换的描述，所以变换后方向保持不变，仅是各个方向投影后有个缩放比例 。
2．特征值的一些另外的属性？如何理解？
答： 在相似变换下不变: 矩阵A和P^-1AP有相同的特征值，这对任何矩阵A和任何可逆矩阵 P都成立。
在转置之下也不变：矩阵A和A^T有相同的特征值。
假设A是一个m×n矩阵，其中m ≤ n，而B是一个n×m矩阵。则BA有和AB相同的特征值。
原因：矩阵是线性空间中的线性变换的一个描述。在一个线性空间中，只要我们选定一组基，那么对于任何一个线性变换，都能够用一个确定的矩阵来加以描述。对于一个线性变换，只要你选定一组基，那么就可以找到一个矩阵来描述这个线性变换。换一组基，就得到一个不同的矩阵。所有这些矩阵都是这同一个线性变换的描述，但又都不是线性变换本身。
定理1 属于不同特征值的特征向量线性无关。
定理2 对于正矩阵 A (A的所有元素为正)，
1）A 的最大特征值是正单根；
2）最大特征值对应所有分量为正的特征向量。

定理3 n阶矩阵A与对角矩阵相似的充分必要条件是A有n个线性无关的特征向量（证明利用特征值和特征向量的表达式定义，对角阵就是以特征值为对角线上元素的矩阵）

十一月 29th, 2011

No comments yet

admin

再谈协方差矩阵之主成分分析

上次那篇文章在理论层次介绍了下协方差矩阵，没准很多人觉得这东西用处不大，其实协方差矩 阵在好多学科里都有很重要的作用，比如多维的正态分布，再比如今天我们今天的主角——主成分分析(Principal Component Analysis，简称PCA)。结合PCA相信能对协方差矩阵有个更深入的认识~
PCA的缘起
PCA大概是198x年提出来的吧，简单的说，它是一种通用的降维工具。在我们处理高维数据的时候，为了能降低后续计算的复杂度，在“预处理”阶段 通常要先对原始数据进行降维，而PCA就是干这个事的。本质上讲，PCA就是将高维的数据通过线性变换投影到低维空间上去，但这个投影可不是随便投投，要 遵循一个指导思想，那就是：找出最能够代表原始数据的投影方法。这里怎么理解这个思想呢？“最能代表原始数据”希望降维后的数据不能失真，也就是说，被PCA降掉的那些维度只能是那些噪声或是冗余的数据。这里的噪声和冗余我认为可以这样认识：

• 噪声：我们常说“噪音污染”，意思就是“噪声”干扰我们想听到的真正声音。同样，假设样本中某个主要的维度 A，它能代表原始数据，是“我们真正想听到的东西”，它本身含有的“能量”(即该维度的方差，为啥？别急，后文该解释的时候就有啦~)本来应该是很大的， 但由于它与其他维度有那么一些千丝万缕的相关性，受到这些个相关维度的干扰，它的能量被削弱了，我们就希望通过PCA处理后，使维度A与其他维度的相关性 尽可能减弱，进而恢复维度A应有的能量，让我们“听的更清楚”！
• 冗余：冗余也就是多余的意思，就是有它没它都一样，放着就是占地方。同样，假如样本中有些个维度，在所有的样 本上变化不明显(极端情况：在所有的样本中该维度都等于同一个数)，也就是说该维度上的方差接近于零，那么显然它对区分不同的样本丝毫起不到任何作用，这 个维度即是冗余的，有它没它一个样，所以PCA应该去掉这些维度。

这么一分析，那么PCA的最终目的就是“降噪”和消灭这些“冗余”的维度，以使降低维度的同时保存数据原有的特征不失真。后面我们将结合例子继续讨论。
协方差矩阵——PCA实现的关键
前面我们说了，PCA的目的就是“降噪”和“去冗余”。“降噪”的目的就是使保留下来的维度间的相关性尽可能小，而“去冗余”的目的就是使保留下来 的维度含有的“能量”即方差尽可能大。那首先的首先，我们得需要知道各维度间的相关性以及个维度上的方差啊！那有什么数据结构能同时表现不同维度间的相关 性以及各个维度上的方差呢？自然是非协方差矩阵莫属。回忆下《浅谈协方差矩阵》的 内容，协方差矩阵度量的是维度与维度之间的关系，而非样本与样本之间。协方差矩阵的主对角线上的元素是各个维度上的方差(即能量)，其他元素是两两维度间 的协方差(即相关性)。我们要的东西协方差矩阵都有了，先来看“降噪”，让保留下的不同维度间的相关性尽可能小，也就是说让协方差矩阵中非对角线元素都基 本为零。达到这个目的的方式自然不用说，线代中讲的很明确——矩阵对角化。而对角化后得到的矩阵，其对角线上是协方差矩阵的特征值，它还有两个身份：首 先，它还是各个维度上的新方差；其次，它是各个维度本身应该拥有的能量(能量的概念伴随特征值而来)。这也就是我们为何在前面称“方差”为“能量”的原 因。也许第二点可能存在疑问，但我们应该注意到这个事实，通过对角化后，剩余维度间的相关性已经减到最弱，已经不会再受“噪声”的影响了，故此时拥有的能 量应该比先前大了。看完了“降噪”，我们的“去冗余”还没完呢。对角化后的协方差矩阵，对角线上较小的新方差对应的就是那些该去掉的维度。所以我们只取那 些含有较大能量(特征值)的维度，其余的就舍掉即可。PCA的本质其实就是对角化协方差矩阵。
下面就让我们跟着上面的感觉来推推公式吧。假设我们有一个样本集X，里面有N个样本，每个样本的维度为d。即：

将这些样本组织成样本矩阵的形式，即每行为一个样本，每一列为一个维度，得到样本矩阵S：。 我们先将样本进行中心化，即保证每个维度的均值为零，只需让矩阵的每一列除以对应的均值即可。很多算法都会先将样本中心化，以保证所有维度上的偏移都是以 零为基点的。然后，对样本矩阵计算其协方差矩阵，按照《浅谈协方差矩阵》里末尾的update，我们知道，协方差矩阵可以简单的按下式计算得到：

下面，根据我们上文的推理，将协方差矩阵C对角化。注意到，这里的矩阵C是是对称矩阵，对称矩阵对角化就是找到一个正交矩阵P，满足：。具体操作是：先对C进行特征值分解，得到特征值矩阵(对角阵)即为，得到特征向量矩阵并正交化即为。显然，。假如我们取最大的前p(p<d)个特征值对应的维度，那么这个p个特征值组成了新的对角阵，对应的p个特征向量组成了新的特征向量矩阵。
实际上，这个新的特征向量矩阵就是投影矩阵，为什么这么说呢？假设PCA降维后的样本矩阵为，显然，根据PCA的目的，中的各个维度间的协方差基本为零，也就是说，的协方差矩阵应该为。即满足：

而我们又有公式：

代入可得：


由于样本矩阵的每一行是一个样本，特征向量矩阵的每一列是一个特征向量。右乘相当于每个样本以的特征向量为基进行线性变换，得到的新样本矩阵中每个样本的维数变为了p，完成了降维操作。实际上，中的特征向量就是低维空间新的坐标系，称之为“主成分”。这就是“主成分分析”的名称由来。同时，的协方差矩阵为近对角阵，说明不同维度间已经基本独立，噪声和冗余的数据已经不见了。至此，整个PCA的过程已经结束，小小总结一下：

1. 形成样本矩阵，样本中心化
2. 计算样本矩阵的协方差矩阵
3. 对协方差矩阵进行特征值分解，选取最大的p个特征值对应的特征向量组成投影矩阵
4. 对原始样本矩阵进行投影，得到降维后的新样本矩阵

Matlab中PCA实战
首先，随机产生一个10*3维的整数矩阵作为样本集，10为样本的个数，3为样本的维数。

1	S = fix(rand(10,3)*50);

计算协方差矩阵：

1 2 3 4

S = S - repmat(mean(S),10,1); C = (S'*S)./(size(S,1)-1); or C = cov(S);

对协方差矩阵进行特征值分解：

1	[P,Lambda] = eig(C);

这里由于三个方差没有明显特别小的，所以我们都保留下来，虽然维度没有降，但观察Lambda(即PCA后的样本协方差矩阵)和C(即原始的协方差矩阵)，可以发现，3个维度上的方差都有增大，也就是能量都比原来增大了，3个维度上的方差有所变化，但对角线之和没有变，能量重新得到了分配，这就是“降噪”的功劳。最后我们得到降维后的样本矩阵：

1

S1 = S*P;

为了验证，我们调用matlab自带的主成分分析函数princomp：

1	[COEFF,SCORE] = princomp(S) % COEFF表示投影矩阵，SCORE表示投影后新样本矩阵

对比，可以发现，SCORE和S1在不考虑维度顺序和正负的情况下是完全吻合的，之所以我们计算的S1的维度顺序不同，是因为通常都是将投影矩阵P 按能量(特征值)的降序排列的，而刚才我们用eig函数得到的结果是升序。另外，在通常的应用中，我们一般是不使用matlab的princomp函数 的，因为它不能真正的降维(不提供相关参数，还是我没发现？)。一般情况下，我们都是按照协方差矩阵分解后特征值所包含的能量来算的，比如取90%的能 量，那就从最大的特征值开始加，一直到部分和占特征值总和的90%为止，此时部分和含有的特征值个数即为p。
经过了一番推公式加敲代码的过程，相信大家对主成分分析应该不陌生了吧，同时对协方差矩阵也有了更深层次的认识了吧，它可不只是花花枪啊。我个人觉得PCA在数学上的理论还是很完备的，想必这也是它能在多种应用中博得鳌头的原因吧。

十一月 22nd, 2011

No comments yet

admin

浅谈协方差矩阵

统计学的基本概念
学过概率统计的孩子都知道，统计里最基本的概念就是样本的均值，方差，或者再加个标准差。首先我们给你一个含有n个样本的集合，依次给出这些概念的公式描述，这些高中学过数学的孩子都应该知道吧，一带而过。
均值：
标准差：
方差：
很显然，均值描述的是样本集合的中间点，它告诉我们的信息是很有限的，而标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均。以这两个 集合为例，[0，8，12，20]和[8，9，11，12]，两个集合的均值都是10，但显然两个集合差别是很大的，计算两者的标准差，前者是8.3，后 者是1.8，显然后者较为集中，故其标准差小一些，标准差描述的就是这种“散布度”。之所以除以n-1而不是除以n，是因为这样能使我们以较小的样本集更 好的逼近总体的标准差，即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。
为什么需要协方差？
上面几个统计量看似已经描述的差不多了，但我们应该注意到，标准差和方差一般是用来描述一维数据的，但现实生活我们常常遇到含有多维数据的数据集， 最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集，我们当然可以按照每一维独立的计算其方差，但是通常我们还想了解更多，比如，一个 男孩子的猥琐程度跟他受女孩子欢迎程度是否存在一些联系啊，嘿嘿~协方差就是这样一种用来度量两个随机变量关系的统计量，我们可以仿照方差的定义：

来度量各个维度偏离其均值的程度，标准差可以这么来定义：

协方差的结果有什么意义呢？如果结果为正值，则说明两者是正相关的(从协方差可以引出“相关系数”的定义)，也就是说一个人越猥琐就越受女孩子欢迎，嘿嘿，那必须的~结果为负值就说明负相关的，越猥琐女孩子越讨厌，可能吗？如果为0，也是就是统计上说的“相互独立”。
从协方差的定义上我们也可以看出一些显而易见的性质，如：


协方差多了就是协方差矩阵
上一节提到的猥琐和受欢迎的问题是典型二维问题，而协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算个协方差，那自然而然的我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

这个定义还是很容易理解的，我们可以举一个简单的三维的例子，假设数据集有三个维度，则协方差矩阵为

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差。
Matlab协方差实战
上面涉及的内容都比较容易，协方差矩阵似乎也很简单，但实战起来就很容易让人迷茫了。必须要明确一点，协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。这个我将结合下面的例子说明，以下的演示将使用Matlab，为了说明计算原理，不直接调用Matlab的cov函数(蓝色部分为Matlab代码)。
首先，随机产生一个10*3维的整数矩阵作为样本集，10为样本的个数，3为样本的维数。

1	MySample = fix(rand(10,3)*50)

根据公式，计算协方差需要计算均值，那是按行计算均值还是按列呢，我一开始就老是困扰这个问题。前面我们也特别强调了，协方差矩阵是计算不同维度间的协方差，要时刻牢记这一点。样本矩阵的每行是一个样本，每列为一个维度，所以我们要按列计算均值。为了描述方便，我们先将三个维度的数据分别赋值：

1	dim1 = MySample(:,1);

2	dim2 = MySample(:,2);

3	dim3 = MySample(:,3);

计算dim1与dim2，dim1与dim3，dim2与dim3的协方差：

1	sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( size(MySample,1)-1 ) % 得到 74.5333

2	sum( (dim1-mean(dim1)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到 -10.0889

3	sum( (dim2-mean(dim2)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到 -106.4000

搞清楚了这个后面就容易多了，协方差矩阵的对角线就是各个维度上的方差，下面我们依次计算：

1	std(dim1)^2 % 得到 108.3222

2	std(dim2)^2 % 得到 260.6222

3	std(dim3)^2 % 得到 94.1778

这样，我们就得到了计算协方差矩阵所需要的所有数据，调用Matlab自带的cov函数进行验证：

1	cov(MySample)

把我们计算的数据对号入座，是不是一摸一样？
Update：今天突然发现，原来协方差矩阵还可以这样计算，先让样本矩阵中心化，即每一维度减去该维度的均值，使每一维度上的均值为0，然后直接用新的到的样本矩阵乘上它的转置，然后除以(N-1)即可。其实这种方法也是由前面的公式通道而来，只不过理解起来不是很直观，但在抽象的公式推导时还是很常用的！同样给出Matlab代码实现：

1	X = MySample - repmat(mean(MySample),10,1); % 中心化样本矩阵，使各维度均值为0

2	C = (X'*X)./(size(X,1)-1);

总结
理解协方差矩阵的关键就在于牢记它计算的是不同维度之间的协方差，而不是不同样本之间，拿到一个样本矩阵，我们最先要明确的就是一行是一个样本还是一个维度，心中明确这个整个计算过程就会顺流而下，这么一来就不会迷茫了~
声明：本文章转自某网站