经典力学中,微观状态对应相空间中的点,包括系统中每个微粒的位置和动量,相空间是包含所有可能微观状态的集合。量子力学中,微观状态(量子态)对应希尔伯特空间中的矢量,希尔伯特空间是包含所有可能微观状态的集合。
又一个巨大的数学反例
【物理科普】热力学第二定律的起源和热力学时间箭头
本文的读者是有一些统计物理学基础但仍然对热力学第二定律的来源感到疑惑的同学。
目前我们所知道的微观世界的物理规律都是可逆【注1】的,但与此同时,热力学第二定告诉我们物理系统在宏观上不可逆,任何处于非平衡态的宏观孤立系统似乎都会不断义无反顾地向熵极大的平衡态演化,没人见过相反的过程。这看上去是一个严重的矛盾:微观上我们已知的所有物理规律都是可逆的,那么宏观上的不可逆性到底是从什么地方冒出来的呢?难道是因为我们所掌握的微观物理规律有错需要修正?如果宏观上如此明显的不可逆性起源于微观物理规律的不可逆性,为什么我们在微观上却从来观查不到?难道说微观物理规律本来只有极其微小的不可逆性以至于我们从未观察到,却由于某种原因在宏观尺度上被剧烈地放大了么?
本文要向同学们说明这样一件事:宏观物理规律的不可逆性完全不必起源于微观物理规律的不可逆性,在微观物理规律完全可逆的前提下,我们照样能看到宏观物理规律的不可逆性,而且这件事情非常自然。
先解释一下两个概念:“宏观状态”、“微观状态”。
经典力学中,微观状态对应相空间中的点,包括系统中每个微粒的位置和动量,相空间是包含所有可能微观状态的集合。量子力学中,微观状态(量子态)对应希尔伯特空间中的矢量,希尔伯特空间是包含所有可能微观状态的集合。如果微观物理规律是可逆的,那么给定物理系统某个时刻的微观状态,物理规律就可以唯一地确定系统未来或过去的状态。
而物理系统的宏观状态则是一组给定的宏观测量仪器(例如温度计、压力表、测距仪、照相机、眼耳鼻舌口皮肤等等)的可分辨状态。如果若干不同的微观状态对于这组仪器完全无法分辨的,就说这这些微观状态都对应同一宏观状态。
因此,宏观热力学状态对具有指定能量的微观状态集(等能量面)构成了一个粗粒划分,等能量面上对应同一宏观状态的所有微观状态构成了一个“状态粗粒”,我们称这种划分为“粗粒化”。粗粒化一般是不均匀的,不同状态粗粒包含的微观状态数量(或体积)多少不一相差极大。最大的宏观状态粗粒就是那个所谓的热平衡状态对应的状态粗粒。
当我们说某个物理系统处于某个宏观状态,其实是说系统所处的微观状态属于对应该宏观状态的那个状态粗粒,但我们并不能确定具体是哪个微观状态。熵就是衡量这种不确定性的大小的量。有统计物理学基础的同学看到这里立即能想到波尔兹曼的熵的微观定义 ,其中
,其中 是熵,
是熵, 是波尔兹曼常数,
是波尔兹曼常数, 是该宏观状态对应的微观状态数【注2】。
是该宏观状态对应的微观状态数【注2】。
不均匀粗粒化的一个直接后果就是:即便微观物理规律完全是可逆的,但由于大的粗粒包含更多的微观状态,因此从小状态粗粒出发进入大状态粗粒的概率就大于相反过程的概率。由于宏观上大状态粗粒对应高熵宏观状态,小状态粗粒对应低熵宏观状态,因此系统从低熵状态出发进入高熵状态的概率就大于相反过程的概率。所以,如果系统最初位于某个熵极低的宏观状态,那么系统就会以极大的概率向高熵宏观状态演化。
也就是说,热力学第二定律来源于粗粒化的非均匀性,而不可逆性则源于宇宙当前所处的低熵状态。
事实上,庞加莱的无限回归定理【注3】表明,只要一个孤立物理系统曾经熵增,经过足够长的时间就一定会熵减。但在绝大部分时间,孤立系统都在熵极大的热平衡态附近来回晃悠(涨落),经过很久很久才会极其罕见但迅速地“不小心”涨落到低熵状态,但接下来就会迅速地回到高熵状态。跟漫长的热平衡阶段相比,低熵状态的阶段只是一些极为短暂的瞬间。对于宇宙来说,这个低熵瞬间的长度都比大爆炸以来的宇宙年龄长得多,而热平衡阶段则不可思议地漫长。
在孤立系统从高熵状态涨落到低熵状态的过程中,熵随着微观物理时间参数(不妨称为“物理时间”)的增加而减少,也就是说此时热力学第二定律所确定的热力学时间箭头跟微观状态演化的物理时间的规定方向相反。既然如此,我们可能看到整个宇宙发生大范围熵减的过程么?很不幸,完全不能。我们的心理时间箭头是由热力学时间箭头决定的,对我们而言宇宙的“过去”总是对应低熵状态,宇宙的“未来”总是对应高熵状态,我们能记住低熵的过去,却记不住高熵的未来。即便宇宙的熵随着物理时间的增加而减少,我们也会把物理时间增加的方向当成过去,把物理时间减少的方向当成未来,以至于只能看到熵增。事实上,微观物理时间的方向规定本来就是随意的,我们完全可以认为今天宇宙的熵正在随着物理时间的增加而减少,但由于我们的心理时间方向跟热力学时间方向相同,以至于我们仍然以为宇宙的熵在增加。
这里有一个很好的类比:无论你在南极还是在北极,你都会发现重力方向是“向下”的,但南极上看来向下的方向在北极上看显然是向上的,既然如此我们站在北极的时候为什么不会认为重力是向上的呢?那是因为我们规定物体下落的方向就是下方,而物体下落的方向恰恰重力方向决定的,所以无论你站在地球上什么地方,你都会认为重力是向下的。同样,无论宇宙的熵随着微观物理时间的流逝增加还是减少,你都会发现时间方向是“向未来”的,因为心理上所谓的“未来”方向恰恰是宇宙的熵增方向决定的。
有人可能会问,既然低熵状态这么罕见,为什么我们今天的宇宙还处于低熵状态?无论低熵状态多么罕见,只要经过足够长(真的非常非常长)的时间,宇宙总是会很“不小心”地涨落回低熵状态,而只有在这些阶段才能存在生命。
微观物理规律的时间可逆性和宏观热力学时间方向性之间,没有任何难以调和的矛盾。
【注1】有些同学可能不清楚『可逆』和『时间反演对称』之间的区别。『时间反演对称』是说系统的物理规律在时间参数取负(t变成-t)时保持形式完全不变,通俗地说如果你给这样的系统拍一段录像,那么倒放这段录像时你看不到任何物理规律被破坏。而『可逆』是说从系统的当前状态不但可以唯一确定后续状态,还可以唯一倒推出先前状态,通俗地说,两个不同微观状态经过一段时间不会变成同一微观状态(信息丢失),一个微观状态经过一段时间也不会不确定地进入两个不同微观状态之一(信息增加)。可逆的系统未必时间反演对称,时间反演对称的系统也未必可逆。在量子力学中,可逆性对应的是“幺正性”。
【注2】在信息论中,概率为 的事件的信息量是
的事件的信息量是 ,而系统的熵定义为所有事件的信息对其发生的概率加权求和:
,而系统的熵定义为所有事件的信息对其发生的概率加权求和: ,如果系统等概率地处于
,如果系统等概率地处于 个状态之一(此时
个状态之一(此时 ),那么系统的熵就是
),那么系统的熵就是  。所以信息论中的熵和统计物理中的熵,除了差一个玻尔兹曼常数
。所以信息论中的熵和统计物理中的熵,除了差一个玻尔兹曼常数 之外,意思是完全相同的。
之外,意思是完全相同的。
【注3】庞加莱无限回归定理:如果等能量面容积有限,那么只要经过足够长的时间,一个孤立物理系统的微观状态将任意次回到任意靠近初始状态的地方。于是物理系统的微观状态实际上可以无数次任意靠近任何一个曾经路过的微观状态。注意,千万不要把无限回归定理和各态历经假设混为一谈,各态历经要求只要经过足够长的时间,一个孤立的物理系统的微观状态将任意次任意靠近等能量面上的任意微观状态。二者的区别是,无线回归可能仅仅对等能量面上的一个连通的子集能够做到各态历经,并不一定对整个等能量面各态历经。
——————————————————————————————————
附:
我用程序模拟运行了一个由若干硬币构成的孤立的玩具动力系统。
其中每个硬币有正面反面两个状态, 个硬币构成的系统有
个硬币构成的系统有 个不同的微观状态,可以由一个
个不同的微观状态,可以由一个 位的二进制串来标记,例如
位的二进制串来标记,例如 。而系统的宏观物理量则是正面硬币的数量(假设我们的宏观仪器只能观测到正面的总数,无法看清每一个硬币的正反面),于是系统对于这套宏观仪器来说有
。而系统的宏观物理量则是正面硬币的数量(假设我们的宏观仪器只能观测到正面的总数,无法看清每一个硬币的正反面),于是系统对于这套宏观仪器来说有 个不同的宏观状态,可以用
个不同的宏观状态,可以用 来标记。显然,有
来标记。显然,有 个正面的宏观状态
个正面的宏观状态 和有
和有 个正面的宏观状态
个正面的宏观状态 对应的微观状态最少,分别只有一个,而正面数量在
对应的微观状态最少,分别只有一个,而正面数量在 或
或 宏观状态对应的微观状态数最多,是
宏观状态对应的微观状态数最多,是 。
。
系统的动力学规律这样设定:对应每一个具体的微观状态,有一个唯一的前驱状态和一个唯一的后续状态,要求前驱和后继状态只有一个硬币的正反与当前状态不同,在这个限制下完全随机设定。对所有的微观状态做了这样的设定之后,状态空间中的2^n个状态通过前驱后续的关系就构成了若干个闭合回路,任意选取其中一个状态迁移的回路,就可以观察系统熵的变化。
下图是一个由 个硬币构成的玩具动力系统的熵变过程,横坐标是物理时间,纵坐标是系统当时的熵。该系统的微观状态数是
个硬币构成的玩具动力系统的熵变过程,横坐标是物理时间,纵坐标是系统当时的熵。该系统的微观状态数是 ,而我们随机构造的状态迁移回路长度为
,而我们随机构造的状态迁移回路长度为 。可以看到,在这个状态回路中,系统大部分时间都游荡在最大熵状态附近,少数情况下系统会游荡到低熵状态,对应图中那个尖尖的深谷。
。可以看到,在这个状态回路中,系统大部分时间都游荡在最大熵状态附近,少数情况下系统会游荡到低熵状态,对应图中那个尖尖的深谷。

如果把硬币数量增加到 ,那么典型的状态回路长度就会变得不可思议地巨大(数量级上与
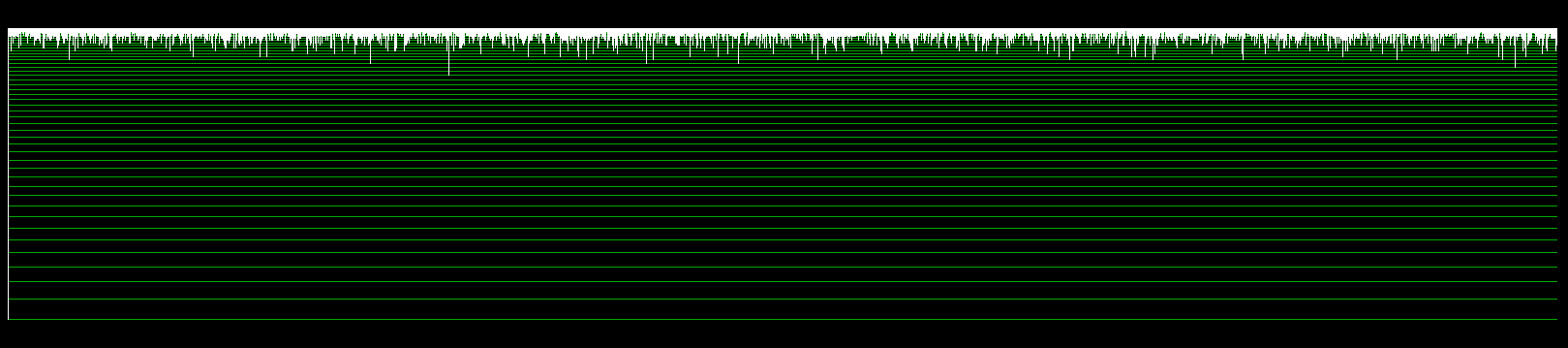
,那么典型的状态回路长度就会变得不可思议地巨大(数量级上与 相差不远),随机生成的动力学状态回路长度会过于巨大以至于我们几乎没可能在有生之年看到一个随机状态回路的完整周期。但我们可以看看这个状态回路中极为短暂的一个低熵瞬间。下图显示了100个硬币构成的动力系统游荡到低熵状态前后约
相差不远),随机生成的动力学状态回路长度会过于巨大以至于我们几乎没可能在有生之年看到一个随机状态回路的完整周期。但我们可以看看这个状态回路中极为短暂的一个低熵瞬间。下图显示了100个硬币构成的动力系统游荡到低熵状态前后约 个时间单位的瞬间。
个时间单位的瞬间。

下图显示了该系统从 熵宏观状态开始的
熵宏观状态开始的 个步骤的熵变,可以看到除了从0熵出发的瞬间,系统始终在最大熵状态附近游荡,我们基本上没可能在有生之年看到该系统再次回到0熵状态。
个步骤的熵变,可以看到除了从0熵出发的瞬间,系统始终在最大熵状态附近游荡,我们基本上没可能在有生之年看到该系统再次回到0熵状态。
目前我们所知道的微观世界的物理规律都是可逆【注1】的,但与此同时,热力学第二定告诉我们物理系统在宏观上不可逆,任何处于非平衡态的宏观孤立系统似乎都会不断义无反顾地向熵极大的平衡态演化,没人见过相反的过程。这看上去是一个严重的矛盾:微观上我们已知的所有物理规律都是可逆的,那么宏观上的不可逆性到底是从什么地方冒出来的呢?难道是因为我们所掌握的微观物理规律有错需要修正?如果宏观上如此明显的不可逆性起源于微观物理规律的不可逆性,为什么我们在微观上却从来观查不到?难道说微观物理规律本来只有极其微小的不可逆性以至于我们从未观察到,却由于某种原因在宏观尺度上被剧烈地放大了么?
本文要向同学们说明这样一件事:宏观物理规律的不可逆性完全不必起源于微观物理规律的不可逆性,在微观物理规律完全可逆的前提下,我们照样能看到宏观物理规律的不可逆性,而且这件事情非常自然。
先解释一下两个概念:“宏观状态”、“微观状态”。
经典力学中,微观状态对应相空间中的点,包括系统中每个微粒的位置和动量,相空间是包含所有可能微观状态的集合。量子力学中,微观状态(量子态)对应希尔伯特空间中的矢量,希尔伯特空间是包含所有可能微观状态的集合。如果微观物理规律是可逆的,那么给定物理系统某个时刻的微观状态,物理规律就可以唯一地确定系统未来或过去的状态。
而物理系统的宏观状态则是一组给定的宏观测量仪器(例如温度计、压力表、测距仪、照相机、眼耳鼻舌口皮肤等等)的可分辨状态。如果若干不同的微观状态对于这组仪器完全无法分辨的,就说这这些微观状态都对应同一宏观状态。
因此,宏观热力学状态对具有指定能量的微观状态集(等能量面)构成了一个粗粒划分,等能量面上对应同一宏观状态的所有微观状态构成了一个“状态粗粒”,我们称这种划分为“粗粒化”。粗粒化一般是不均匀的,不同状态粗粒包含的微观状态数量(或体积)多少不一相差极大。最大的宏观状态粗粒就是那个所谓的热平衡状态对应的状态粗粒。
当我们说某个物理系统处于某个宏观状态,其实是说系统所处的微观状态属于对应该宏观状态的那个状态粗粒,但我们并不能确定具体是哪个微观状态。熵就是衡量这种不确定性的大小的量。有统计物理学基础的同学看到这里立即能想到波尔兹曼的熵的微观定义
不均匀粗粒化的一个直接后果就是:即便微观物理规律完全是可逆的,但由于大的粗粒包含更多的微观状态,因此从小状态粗粒出发进入大状态粗粒的概率就大于相反过程的概率。由于宏观上大状态粗粒对应高熵宏观状态,小状态粗粒对应低熵宏观状态,因此系统从低熵状态出发进入高熵状态的概率就大于相反过程的概率。所以,如果系统最初位于某个熵极低的宏观状态,那么系统就会以极大的概率向高熵宏观状态演化。
也就是说,热力学第二定律来源于粗粒化的非均匀性,而不可逆性则源于宇宙当前所处的低熵状态。
事实上,庞加莱的无限回归定理【注3】表明,只要一个孤立物理系统曾经熵增,经过足够长的时间就一定会熵减。但在绝大部分时间,孤立系统都在熵极大的热平衡态附近来回晃悠(涨落),经过很久很久才会极其罕见但迅速地“不小心”涨落到低熵状态,但接下来就会迅速地回到高熵状态。跟漫长的热平衡阶段相比,低熵状态的阶段只是一些极为短暂的瞬间。对于宇宙来说,这个低熵瞬间的长度都比大爆炸以来的宇宙年龄长得多,而热平衡阶段则不可思议地漫长。
在孤立系统从高熵状态涨落到低熵状态的过程中,熵随着微观物理时间参数(不妨称为“物理时间”)的增加而减少,也就是说此时热力学第二定律所确定的热力学时间箭头跟微观状态演化的物理时间的规定方向相反。既然如此,我们可能看到整个宇宙发生大范围熵减的过程么?很不幸,完全不能。我们的心理时间箭头是由热力学时间箭头决定的,对我们而言宇宙的“过去”总是对应低熵状态,宇宙的“未来”总是对应高熵状态,我们能记住低熵的过去,却记不住高熵的未来。即便宇宙的熵随着物理时间的增加而减少,我们也会把物理时间增加的方向当成过去,把物理时间减少的方向当成未来,以至于只能看到熵增。事实上,微观物理时间的方向规定本来就是随意的,我们完全可以认为今天宇宙的熵正在随着物理时间的增加而减少,但由于我们的心理时间方向跟热力学时间方向相同,以至于我们仍然以为宇宙的熵在增加。
这里有一个很好的类比:无论你在南极还是在北极,你都会发现重力方向是“向下”的,但南极上看来向下的方向在北极上看显然是向上的,既然如此我们站在北极的时候为什么不会认为重力是向上的呢?那是因为我们规定物体下落的方向就是下方,而物体下落的方向恰恰重力方向决定的,所以无论你站在地球上什么地方,你都会认为重力是向下的。同样,无论宇宙的熵随着微观物理时间的流逝增加还是减少,你都会发现时间方向是“向未来”的,因为心理上所谓的“未来”方向恰恰是宇宙的熵增方向决定的。
有人可能会问,既然低熵状态这么罕见,为什么我们今天的宇宙还处于低熵状态?无论低熵状态多么罕见,只要经过足够长(真的非常非常长)的时间,宇宙总是会很“不小心”地涨落回低熵状态,而只有在这些阶段才能存在生命。
微观物理规律的时间可逆性和宏观热力学时间方向性之间,没有任何难以调和的矛盾。
【注1】有些同学可能不清楚『可逆』和『时间反演对称』之间的区别。『时间反演对称』是说系统的物理规律在时间参数取负(t变成-t)时保持形式完全不变,通俗地说如果你给这样的系统拍一段录像,那么倒放这段录像时你看不到任何物理规律被破坏。而『可逆』是说从系统的当前状态不但可以唯一确定后续状态,还可以唯一倒推出先前状态,通俗地说,两个不同微观状态经过一段时间不会变成同一微观状态(信息丢失),一个微观状态经过一段时间也不会不确定地进入两个不同微观状态之一(信息增加)。可逆的系统未必时间反演对称,时间反演对称的系统也未必可逆。在量子力学中,可逆性对应的是“幺正性”。
【注2】在信息论中,概率为
【注3】庞加莱无限回归定理:如果等能量面容积有限,那么只要经过足够长的时间,一个孤立物理系统的微观状态将任意次回到任意靠近初始状态的地方。于是物理系统的微观状态实际上可以无数次任意靠近任何一个曾经路过的微观状态。注意,千万不要把无限回归定理和各态历经假设混为一谈,各态历经要求只要经过足够长的时间,一个孤立的物理系统的微观状态将任意次任意靠近等能量面上的任意微观状态。二者的区别是,无线回归可能仅仅对等能量面上的一个连通的子集能够做到各态历经,并不一定对整个等能量面各态历经。
——————————————————————————————————
附:
我用程序模拟运行了一个由若干硬币构成的孤立的玩具动力系统。
其中每个硬币有正面反面两个状态,
系统的动力学规律这样设定:对应每一个具体的微观状态,有一个唯一的前驱状态和一个唯一的后续状态,要求前驱和后继状态只有一个硬币的正反与当前状态不同,在这个限制下完全随机设定。对所有的微观状态做了这样的设定之后,状态空间中的2^n个状态通过前驱后续的关系就构成了若干个闭合回路,任意选取其中一个状态迁移的回路,就可以观察系统熵的变化。
下图是一个由

如果把硬币数量增加到

下图显示了该系统从

2 Comments