维基百科,自由的百科全书
量子力學中,以自旋物理與核磁共振專家菲力·布洛赫(Felix Bloch)姓氏為名的布洛赫球面乃一種對於雙態系統之純態空間的幾何表示法。在討論量子位元的場合上常常運用到。
 (採狄拉克標記的右括向量表示)可以由兩個互相正交的基底以複數線性疊加所構成,這兩個基底可以選用
(採狄拉克標記的右括向量表示)可以由兩個互相正交的基底以複數線性疊加所構成,這兩個基底可以選用 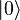 和
和 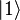 為代表。在物理實作上,
為代表。在物理實作上,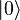 和
和 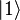 代表了做投影式量子測量所會得到的唯二結果。
代表了做投影式量子測量所會得到的唯二結果。
從任意純態出發: ,其中
,其中 。
。
故可設:
 稱作共同相位(global phase),因為對
稱作共同相位(global phase),因為對 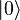 、對
、對 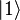 都一樣影響,而在實驗上測量不出來,故可以將之捨棄不看。
都一樣影響,而在實驗上測量不出來,故可以將之捨棄不看。
至於相對相位(relative phase) 就不同了,它的影響可以在球面上表現出來。故得:
就不同了,它的影響可以在球面上表現出來。故得:
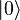 的係數
的係數  是實數,並且
是實數,並且  在原先
在原先  所代表的是複數
所代表的是複數  的長度(模、幅值,amplitude),故
的長度(模、幅值,amplitude),故  結果要是非負實數;
結果要是非負實數; 亦是如此道理。故可定出
亦是如此道理。故可定出  與
與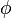 的範圍如下:
的範圍如下:
 和
和 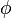 的所有分佈在三維空間
的所有分佈在三維空間  中畫出來,就可以得到一個球面,此即布洛赫球面,如同圖1。
中畫出來,就可以得到一個球面,此即布洛赫球面,如同圖1。
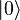 和
和 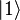 在此幾何表示法下成為一軸的兩端,變成180度關係,此乃因
在此幾何表示法下成為一軸的兩端,變成180度關係,此乃因  的緣故。通常設定它們處在
的緣故。通常設定它們處在  軸,即:
軸,即:
 之定義為:
之定義為:
此種表示法的用意在使布洛赫球面上 表示方式和一般
表示方式和一般  中的球面以極坐標
中的球面以極坐標  表示方式呈現一致。
表示方式呈現一致。
目录[隐藏] |
[编辑] 布洛赫球面諸點與純態的對應
對量子位元這樣的二階量子系統而言,其存在的可能狀態 (採狄拉克標記的右括向量表示)可以由兩個互相正交的基底以複數線性疊加所構成,這兩個基底可以選用
(採狄拉克標記的右括向量表示)可以由兩個互相正交的基底以複數線性疊加所構成,這兩個基底可以選用 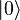 和
和 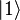 為代表。在物理實作上,
為代表。在物理實作上,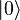 和
和 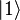 代表了做投影式量子測量所會得到的唯二結果。
代表了做投影式量子測量所會得到的唯二結果。從任意純態出發:
 ,其中
,其中 。
。故可設:
其中

 稱作共同相位(global phase),因為對
稱作共同相位(global phase),因為對 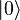 、對
、對 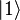 都一樣影響,而在實驗上測量不出來,故可以將之捨棄不看。
都一樣影響,而在實驗上測量不出來,故可以將之捨棄不看。至於相對相位(relative phase)
 就不同了,它的影響可以在球面上表現出來。故得:
就不同了,它的影響可以在球面上表現出來。故得:可以看到
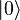 的係數
的係數  是實數,並且
是實數,並且  在原先
在原先  所代表的是複數
所代表的是複數  的長度(模、幅值,amplitude),故
的長度(模、幅值,amplitude),故  結果要是非負實數;
結果要是非負實數; 亦是如此道理。故可定出
亦是如此道理。故可定出  與
與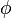 的範圍如下:
的範圍如下:將

 和
和 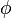 的所有分佈在三維空間
的所有分佈在三維空間  中畫出來,就可以得到一個球面,此即布洛赫球面,如同圖1。
中畫出來,就可以得到一個球面,此即布洛赫球面,如同圖1。可以注意到正交(意義上有「垂直,呈90度關係」之意涵)的兩個基底
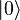 和
和 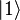 在此幾何表示法下成為一軸的兩端,變成180度關係,此乃因
在此幾何表示法下成為一軸的兩端,變成180度關係,此乃因  的緣故。通常設定它們處在
的緣故。通常設定它們處在  軸,即:
軸,即: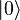 是
是 、
、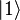 是
是 ,
,
[编辑] 習慣差異
有些學者及書刊對於球面所採用的表示為:角度範圍:
是故,其狀態
 之定義為:
之定義為:此種表示法的用意在使布洛赫球面上
 表示方式和一般
表示方式和一般  中的球面以極坐標
中的球面以極坐標  表示方式呈現一致。
表示方式呈現一致。[编辑] 布洛赫球與混態
布洛赫球(Bloch ball)是布洛赫球面的擴充,混態(mixed state)會出現在球內而不是球面上,亦即離球心距離<1的點。並可從此推論出球心該點所代表的量子狀態是混合最全態(maximally mixed state),用密度矩陣形式及狄拉克標記表示即(另見「量子位元」):



 。
。


No comments:
Post a Comment