| 全文檢索 | 科學人小字典 |
粒子物理與幾何的對話
鞏訥的非可換幾何提供了有別於弦論的另一種架構，由於鞏訥的理論可以直接用實驗來檢驗，所以或許比弦論還棒。
撰文／赫勒曼斯（Alexander Hellemans）
翻譯／高涌泉
鞏訥：重新定義空間
■他是非可換幾何的主要發明者，這種新幾何是一種數學空間，在此空間中，事件的順序比物體的位置更重要。
■他說明可換幾何的起源：最棒的事在於，人們透過實驗與理論研究所獲得的結果，居然有意想不到的數學之美。
在瑞士日內瓦附近的高能粒子加速器：大型強子對撞機（Large Hadron Collider, LHC）明年就要啟動了，如果有數學家也和物理學家一樣，急切地等著LHC的結果，那一定就是巴黎法蘭西學院的鞏訥（Alain Connes）了。他和許多物理學家一樣，希望LHC的偵測器會找到希格斯粒子（Higgs particle）。在所謂標準模型，也就是描述基本粒子與其交互作用的理論架構中，希格斯粒子是最後一個還沒找到的關鍵元素；按道理，希格斯粒子能賦予其他粒子質量。對鞏訥來說，找到希格斯粒子是很重要的，因為希格斯粒子──甚至其質量──會出現在一種新型數學的奇特方程式中；這種新型數學稱為「非可換幾何」（noncommutative geometry），而鞏訥就是主要的發明者。
鞏訥的想法是將幾何空間與其卡式座標（即一般常用的直角座標）的可換代數，推廣到一種奠基於非可換代數的幾何。在可換代數中，兩數的乘積和相乘時的順序沒有關係，例如3×5＝5×3。但是有些運作是不可以交換其順序的。以一架可以又翻（繞著縱軸旋轉）又滾（繞著與機翼平行的軸旋轉）的特技飛機為例，如果飛行員接到無線電指示先翻90度，接著再朝飛機底部滾90度，那麼只要飛行員依據指示的順序操作，一切就都沒問題。但是如果順序顛倒了，則飛機就會筆直往下掉。卡氏座標中的運作是可換的，而三維空間中的旋轉是不可換的。
物理學家為了更清楚地理解自然現象，他們有時會使用所謂的「相空間」。這種空間和卡氏座標不一樣，例如它會顯示電子的速度和動量，而非只是電子的x座標與y座標而已。由於海森堡的測不準原理，我們無法同時測量速度與動量，所以位置乘上動量並不會等於動量乘上位置，因此量子相空間是非可換空間。此外，我們如果把這種非可換性質引入一般空間中，例如讓x座標與y座標變成非可換座標，那麼就造出了一個帶有非可換幾何的空間。
鞏訥透過這樣的分析，發現了這種新型幾何的奇特性質，這些性質對應到量子理論的原理。他花了30年的時間來改進他的想法。即使他已將此學問的基本觀念寫成書，發表於1994年，研究人員還是蜂擁而至來聽他演講。3月的某個風雨日，大約60名頂尖法國數學家擠滿了法蘭西學院第五號教室，59歲的鞏訥在兩座投影機間快速地走來走去，像頭籠中的獅子。他講得很快，不停地將寫滿方程式的投影片換上換下。在外頭，警車的號笛在抗議學生群中響起，這些學生想佔領隔壁的索本大學，以抗議法國政府所提議的新就業法。
鞏訥似乎毫不在意這些騷動，即使在演講過後，當他走過藍色的警方箱型車與鎮暴警察、跨過聖賈克路時，他仍不停談論他的研究如何導致物理新概念。他舉粒子物理的發展方式為例：愛因斯坦的時空觀源自電動力學，但是電動力學只是標準模型的一小部份而已，如果人們發現有必要放進新粒子，則新粒子就會被加到標準模型中，一旦這些預測的粒子在加速器中出現，標準模型就獲得證實。
但是同樣奠基於電動力學的廣義相對論，時空觀卻沒有被物理學家修改。鞏訥提出了相當不一樣的想法：「與其引入新粒子，不如使用一種更微妙的幾何，而這些新粒子會自動出現在新幾何的結構中。」事實上，鞏訥已經成功創造了一種非可換空間，它包含了所有用來描述標準模型中基本粒子的抽象代數（也稱為對稱群）。
所以從標準模型所衍生出來的圖像便是：物理時空乃是一種非可換空間，此空間由兩層連續體所組成，就像一張紙的兩面。介於這張紙兩面之間的空間是一個額外的、離散的（不連續的）非可換空間。整個空間中離散的這一部份產生了希格斯粒子，而連續體那一部份則產生了規範玻色子，例如傳遞弱力的W粒子與Z粒子。
SO(3)上的卡■他是非可換幾何的主要發明者，這種新幾何是一種數學空間，在此空間中，事件的順序比物體的位置更重要。
■他說明可換幾何的起源：最棒的事在於，人們透過實驗與理論研究所獲得的結果，居然有意想不到的數學之美。
在瑞士日內瓦附近的高能粒子加速器：大型強子對撞機（Large Hadron Collider, LHC）明年就要啟動了，如果有數學家也和物理學家一樣，急切地等著LHC的結果，那一定就是巴黎法蘭西學院的鞏訥（Alain Connes）了。他和許多物理學家一樣，希望LHC的偵測器會找到希格斯粒子（Higgs particle）。在所謂標準模型，也就是描述基本粒子與其交互作用的理論架構中，希格斯粒子是最後一個還沒找到的關鍵元素；按道理，希格斯粒子能賦予其他粒子質量。對鞏訥來說，找到希格斯粒子是很重要的，因為希格斯粒子──甚至其質量──會出現在一種新型數學的奇特方程式中；這種新型數學稱為「非可換幾何」（noncommutative geometry），而鞏訥就是主要的發明者。
鞏訥的想法是將幾何空間與其卡式座標（即一般常用的直角座標）的可換代數，推廣到一種奠基於非可換代數的幾何。在可換代數中，兩數的乘積和相乘時的順序沒有關係，例如3×5＝5×3。但是有些運作是不可以交換其順序的。以一架可以又翻（繞著縱軸旋轉）又滾（繞著與機翼平行的軸旋轉）的特技飛機為例，如果飛行員接到無線電指示先翻90度，接著再朝飛機底部滾90度，那麼只要飛行員依據指示的順序操作，一切就都沒問題。但是如果順序顛倒了，則飛機就會筆直往下掉。卡氏座標中的運作是可換的，而三維空間中的旋轉是不可換的。
物理學家為了更清楚地理解自然現象，他們有時會使用所謂的「相空間」。這種空間和卡氏座標不一樣，例如它會顯示電子的速度和動量，而非只是電子的x座標與y座標而已。由於海森堡的測不準原理，我們無法同時測量速度與動量，所以位置乘上動量並不會等於動量乘上位置，因此量子相空間是非可換空間。此外，我們如果把這種非可換性質引入一般空間中，例如讓x座標與y座標變成非可換座標，那麼就造出了一個帶有非可換幾何的空間。
鞏訥透過這樣的分析，發現了這種新型幾何的奇特性質，這些性質對應到量子理論的原理。他花了30年的時間來改進他的想法。即使他已將此學問的基本觀念寫成書，發表於1994年，研究人員還是蜂擁而至來聽他演講。3月的某個風雨日，大約60名頂尖法國數學家擠滿了法蘭西學院第五號教室，59歲的鞏訥在兩座投影機間快速地走來走去，像頭籠中的獅子。他講得很快，不停地將寫滿方程式的投影片換上換下。在外頭，警車的號笛在抗議學生群中響起，這些學生想佔領隔壁的索本大學，以抗議法國政府所提議的新就業法。
鞏訥似乎毫不在意這些騷動，即使在演講過後，當他走過藍色的警方箱型車與鎮暴警察、跨過聖賈克路時，他仍不停談論他的研究如何導致物理新概念。他舉粒子物理的發展方式為例：愛因斯坦的時空觀源自電動力學，但是電動力學只是標準模型的一小部份而已，如果人們發現有必要放進新粒子，則新粒子就會被加到標準模型中，一旦這些預測的粒子在加速器中出現，標準模型就獲得證實。
但是同樣奠基於電動力學的廣義相對論，時空觀卻沒有被物理學家修改。鞏訥提出了相當不一樣的想法：「與其引入新粒子，不如使用一種更微妙的幾何，而這些新粒子會自動出現在新幾何的結構中。」事實上，鞏訥已經成功創造了一種非可換空間，它包含了所有用來描述標準模型中基本粒子的抽象代數（也稱為對稱群）。
所以從標準模型所衍生出來的圖像便是：物理時空乃是一種非可換空間，此空間由兩層連續體所組成，就像一張紙的兩面。介於這張紙兩面之間的空間是一個額外的、離散的（不連續的）非可換空間。整個空間中離散的這一部份產生了希格斯粒子，而連續體那一部份則產生了規範玻色子，例如傳遞弱力的W粒子與Z粒子。
维基百科，自由的百科全书
在数学中，三维空间内的特殊正交群，也被称为旋转群的SO(3)，是一个典型的流形。在不同的SO(3)上的卡中，建立的坐标系互不相同:从这个角度讲，不能说哪种参数很适合描述旋转。由于存在三个自由度，因此SO(3)的维数是3。在不同的应用中需要使用不同的坐标系，因此如何从一个坐标系转换到另一个坐标系是一个潜在的问题。
两个旋转的符合是一个新的旋转；每个旋转都有唯一的逆旋转；且存在幺元（单位矩阵）。基于上面这些性质，所有旋转矩阵组成的集合是拥有复合操作的群。而且，旋转群因其操作是光滑的而具有天然的流形结构；因此，它也是一个李群。旋转群经常用SO(3)表示，其原因将在下面解释。
旋转空间与旋转操作以及“行列式为1的正交矩阵”之间是拓扑同构的。它还与内积操作下的四元数表示，以旋转向量和由其对应矩阵构建的复合操作构成的空间同构。
旋转的向量表示法最开始来源于欧拉旋转定理中描述的任何三维空间中的旋转都可以用一系列旋转轴和旋转角来表示。这样，我们可以用球面坐标的两个角度表示旋转轴，再用向量的长度表示旋转角。这些向量就构成了在三维空间内的具有特殊拓扑结构的球。
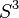，也就是四维欧几里得空间内的圆盘的边界。我们首先要用四维嵌入曲面上的点表示一个旋转。
用半径来表示旋转角度的方法并不是显而易见的。这和在球体上定义北极点后形成的纬度线有关，在下面会详细解释。
我们用三维空间球体的北极点作为单位旋转的对应点。对于单位旋转来说，无法定义旋转轴，旋转角度（0）也是无关紧要的。对应于一个非常小转角的旋转可以用平行于xy平面，并且非常接近于北极点的一个小横截面表示。由这个横截面产生的圆非常的小，对应于小的旋转角。当旋转角度变大时，横截面向南移动，圆的半径一直变大直到到达球体的赤道，对应于180度的旋转角。继续往南移动，圆的半径会变小，对应于旋转角度的绝对值变小。最终，到达南极点之后，圆环又归于一点。虽然这里只考虑xy平面内的旋转，通过这种可视化，三维旋转的很多特性和表示方法都可以显示出来。
旋转矩阵式连续的，每个旋转都有一个与其几乎相同的近邻，当取的近邻足够小时变成平的。
两个连续的绕xy平面内转轴的旋转的复合不一定形成一个转轴在xy平面内的旋转，因此这个旋转就不能在三维球面上表示了。这和三维空间内的旋转不同，其旋转在复合下是封闭的。
这种可视化可以扩展到三维空间的旋转。单位旋转式一个点，一个小角度的旋转可以表示为一个小半径的球面。当旋转的角度增大时，球面也变大，知道旋转角度到达180度，从这里开始球面开始随角度变大而收缩，到360度时重新回到一个点（也可以理解为负向的0度）。这一系列扩张和收缩的球面组成了四维空间内的超球面（一个三维球面）。
就像绕xy平面轴旋转的简单例子一样，每个超球面上点都和其对极点想对应。超球面的“纬度”代表着旋转角度的一半，随着领域每个点的领域都变得越来越“平”（可以利用三维欧几里得空间的点表示）。
这种现象与用单位四元数表示旋转的方式相吻合：一个四元数代表四维空间内的一个点，将其长度约束为1后就可以得到四维空间的球面，也就是一个三维空间。单位四元数具有单位长度，对应于超球面的单位半径。
单位四元数的向量部分表示旋转轴所对应的二维球面，其强度对应于旋转角度一半的正弦值。每个旋转都可以用两个符号相反的单位四元数表示，而且对于三维旋转空间来说，两个单位四元数的四元积产生一个新的单位四元数。另外，当领域无穷小时，单位四元数空间也变得越来越“平”。
目录[隐藏] |
[编辑] 旋转空间
在几何中，旋转群是所有关于三维欧几里得空间R3原点的，具有复合函数的旋转矩阵组成的群。[1] 根据定义，关于原点的旋转是保持向量的长度和空间方向（即左旋或右旋）不变的线性变换。保持长度不变而逆转方向的变换叫做非合理旋转。三维欧几里得空间内在正常旋转后面接着做关于经过原点平面的反射。两个旋转的符合是一个新的旋转；每个旋转都有唯一的逆旋转；且存在幺元（单位矩阵）。基于上面这些性质，所有旋转矩阵组成的集合是拥有复合操作的群。而且，旋转群因其操作是光滑的而具有天然的流形结构；因此，它也是一个李群。旋转群经常用SO(3)表示，其原因将在下面解释。
旋转空间与旋转操作以及“行列式为1的正交矩阵”之间是拓扑同构的。它还与内积操作下的四元数表示，以旋转向量和由其对应矩阵构建的复合操作构成的空间同构。
旋转的向量表示法最开始来源于欧拉旋转定理中描述的任何三维空间中的旋转都可以用一系列旋转轴和旋转角来表示。这样，我们可以用球面坐标的两个角度表示旋转轴，再用向量的长度表示旋转角。这些向量就构成了在三维空间内的具有特殊拓扑结构的球。
[编辑] 旋转超球面
[编辑] 可视化超球体
我们可以把所有绕xy平面内轴旋转构成的空间当成三维空间内的球体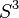，也就是四维欧几里得空间内的圆盘的边界。我们首先要用四维嵌入曲面上的点表示一个旋转。用半径来表示旋转角度的方法并不是显而易见的。这和在球体上定义北极点后形成的纬度线有关，在下面会详细解释。
我们用三维空间球体的北极点作为单位旋转的对应点。对于单位旋转来说，无法定义旋转轴，旋转角度（0）也是无关紧要的。对应于一个非常小转角的旋转可以用平行于xy平面，并且非常接近于北极点的一个小横截面表示。由这个横截面产生的圆非常的小，对应于小的旋转角。当旋转角度变大时，横截面向南移动，圆的半径一直变大直到到达球体的赤道，对应于180度的旋转角。继续往南移动，圆的半径会变小，对应于旋转角度的绝对值变小。最终，到达南极点之后，圆环又归于一点。虽然这里只考虑xy平面内的旋转，通过这种可视化，三维旋转的很多特性和表示方法都可以显示出来。
旋转矩阵式连续的，每个旋转都有一个与其几乎相同的近邻，当取的近邻足够小时变成平的。
[编辑] 别名
另外，每个旋转都可以用球面上的两个对极点表示，就是通过球心的连线的另一端。这表明每个旋转都可以用关于某个轴旋转某个角度，或者关于相反的轴旋转相反的角度（就是所谓的复叠）。圆环所处的“纬度”是旋转角度的一般，因为从北极到南极，纬度值一共改变了180度，而旋转的角度可以从0度到360度。“经度”则用来表示xy平面内的转轴。但是这样形成的旋转集合并不是封闭的。两个连续的绕xy平面内转轴的旋转的复合不一定形成一个转轴在xy平面内的旋转，因此这个旋转就不能在三维球面上表示了。这和三维空间内的旋转不同，其旋转在复合下是封闭的。
这种可视化可以扩展到三维空间的旋转。单位旋转式一个点，一个小角度的旋转可以表示为一个小半径的球面。当旋转的角度增大时，球面也变大，知道旋转角度到达180度，从这里开始球面开始随角度变大而收缩，到360度时重新回到一个点（也可以理解为负向的0度）。这一系列扩张和收缩的球面组成了四维空间内的超球面（一个三维球面）。
就像绕xy平面轴旋转的简单例子一样，每个超球面上点都和其对极点想对应。超球面的“纬度”代表着旋转角度的一半，随着领域每个点的领域都变得越来越“平”（可以利用三维欧几里得空间的点表示）。
这种现象与用单位四元数表示旋转的方式相吻合：一个四元数代表四维空间内的一个点，将其长度约束为1后就可以得到四维空间的球面，也就是一个三维空间。单位四元数具有单位长度，对应于超球面的单位半径。
单位四元数的向量部分表示旋转轴所对应的二维球面，其强度对应于旋转角度一半的正弦值。每个旋转都可以用两个符号相反的单位四元数表示，而且对于三维旋转空间来说，两个单位四元数的四元积产生一个新的单位四元数。另外，当领域无穷小时，单位四元数空间也变得越来越“平”。
更多相關資訊
- 1.找到了希格斯粒子之後
- 2.真相揭曉的時刻到了
- 3.費曼大師的小失誤
- 4.電動力學與相對性原理
- 5.改變歷史的人
- 6.科學教育必須注重閱讀與敘事能力
- 7.地球自轉：多姿多采的旋舞
- 8.為什麼不是圓？
- 9.1609
- 10.站在生物學邊上的物理學家
- 11.伸卡球魔力何來？—變化球密技大解析
- 12.重力為什麼會影響時間？在黑洞裡時間會停止嗎？
No comments:
Post a Comment