量子的誕生
近代物理的兩個常數
凱爾文所說的兩朵烏雲
牛頓力學在十七世紀建立古典力學,科學進入新階段,牛頓三大定律及萬有引力公式解釋了所有天文觀察到的現象。之後的兩百年,科學家依牛頓力學的模式建立了聲學、熱學等物理學門。兩朵小烏雲竟帶來大風暴的物理革命
凱爾文因此說:"在己建立的科學大廈中,後世的科學只能作一些零碎修補的工作"。然而,他也指出 "在物理學睛朗的天空遠處,還有兩朵令人不安的小小烏雲" 。他指的一個是找尋以太卻總是失敗,另一個則是熱幅射的實驗之無法解釋。
光速-變成常數 -> 相對論
普朗克常數 -> 量子論
普朗克常數
凝體的熱幅射
以下為鐵塊一端加熱後之模擬畫面
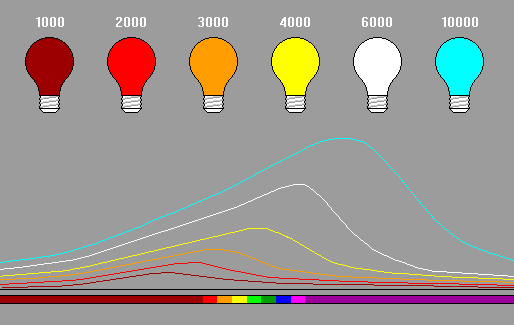
溫度與顏色的簡化示意圖
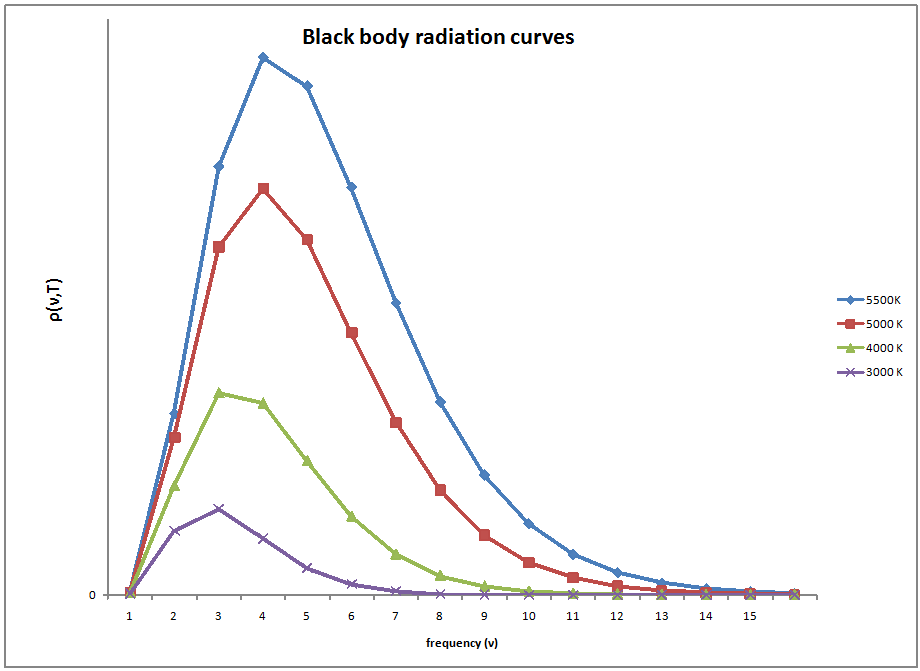
(高檔螢幕可調"色溫")頻率作橫軸
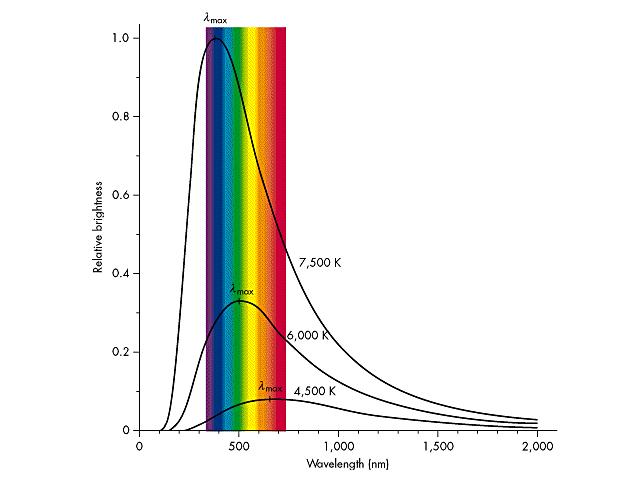
以波長作橫軸
為什麼要研究這個?當時世界大戰前的局勢,鍊鋼為重要技術,希望有由顏色(光譜)精確測得測量溫度的方法。(量額溫所用的原理相同)
理想化的模型-黑體
一般而言,熱幅射光譜裏的微細結構與熱體的組成物質種類有關,但從實驗知道有一類的熱體則呈現共同的熱幅射光譜形狀,它們被稱作是黑體,其表面因對各種波長的光皆吸收而呈現黑色。實作的情況,可以在物體的外表覆蓋一層黑炭灰,即成為黑體。古典熱力學可說明凡是黑體都有相同的幅射能量與頻率關係分佈形式(即光譜),但卻無從說明實驗上量到的形狀為何是那樣(與預測差蠻多的,見後)。黑體幅射與空腔幅射
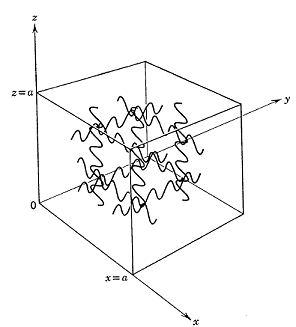
另有一個黑體的例子,對於理論探討特別有幫助,即一個理想的空腔。
古典理論
如何看上面的實驗結果?不同頻率(或波長)波段的能量互相交換,所累積多寡不一樣,形式一個分佈,而此分佈的形狀隨溫度改變。
能量均分原理
在平衡的情況下,每個自由度會分到一樣的能量 1/2 kT。簡諧振子的系統,位能部分會和動能部分會分到一樣多的能量,因此兩個 1/2 kT 合起來就是一個 kT 了。
每個駐波 mode 會是一個自由度嗎?每個 normal mode 就之一個自由度(N 個粒子,即 3N 自由度的系統會產生 3N 個 normal mode) 。各自獨立的鈍氣原子氣體是如此、雙原子分子構成的氣體是如此(詳見雙原子分子氣體的比熱問題)、全部原子都互相吸引而內聚的液體,或原子間以鍵結固定起來而只剩振動的固體,也都遵守這個能量均分原理。
在此提供一個圖像,試想,用彈簧一個接一個串起來的質量塊,將一塊拉離其平衡位置後立即釋放,問振動會留在那顆被拉以及附近的質量塊?還是會遍及所有的質量塊?答案是,能量會散佈分配到所有可能的模式中。
電腦模擬(自行習作):以彈簧-質量串列來模擬能量均分現象
延伸議題:Fermi–Pasta–Ulam
分析並算計駐波模式
將上述觀念用在空腔幅射內的駐波(駐波是空腔內電磁波唯一可持續存在的振動模式),一種可能的駐波就是一個 normal mode,一個獨立的自由度,因此根據能量均分原理,它只能分到一份 1/2 kT 的能量。現在我們有一個可以評估各頻率(波長)釋放多少能量的基礎了,我們只需要分析每種特定頻率能在空腔中建立多少不同的駐波模式,若多,則該頻率分到的能量就多,若少,分到的能量就少。
這樣所分析出來的 (不正確的) 能量密度分佈為
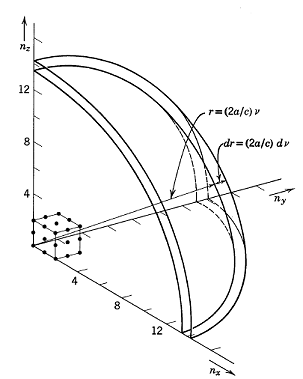
(1) 純幾何
(2) ν 與 EM 能量ε關係 ? 無關 !
如此, 得 mode number 為
請注意上式所句有的頻率平方屬性
根據統計力學,波玆曼分佈描述了力學系統之能量ε與溫度 T 如何決定該狀態出現的機率 P :
其中的振子能量 ε ,對某頻率電磁波而言(它是一個 SHO,動能得 1/2 、位能得 1/2,故為 kT。另外,它是一個橫波,故有兩個自由度),其在溫度 T 時的平均能量是
(即事件發生之機率,與該事件總能量及當時整個系統溫度有關)
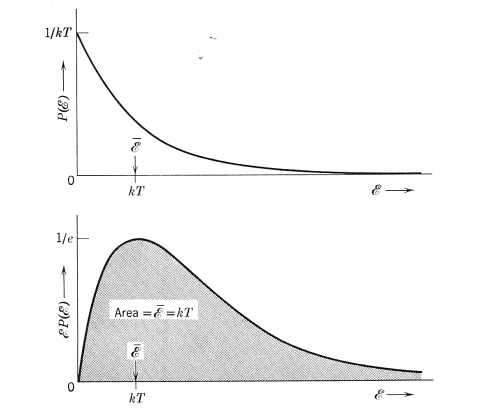
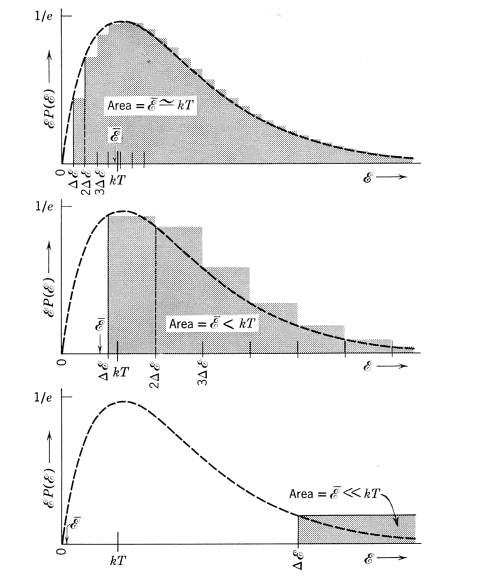
如下二圖 (上 : 能量分佈的機率密度函數, 下 : 能量乘上能量分佈的機率密度函數, 總和起來是平均能量)
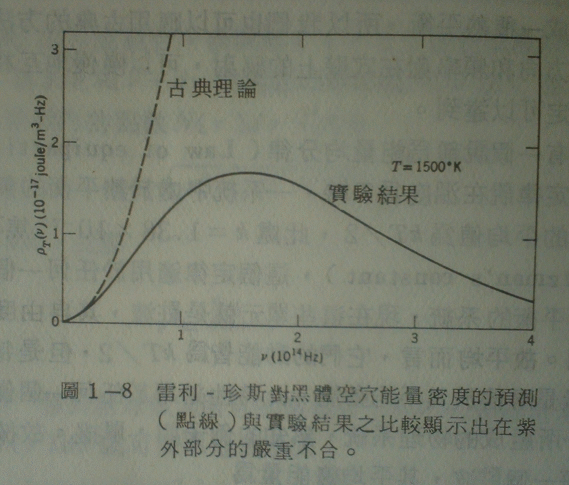
古典理論的問題
Mode number 與普朗克的改造
Rayleigh-Jeans 公式
Stefan–Boltzmann law上圖錯得這樣離譜, 但使用的物理又如此基本, 想必有重要關鍵被忽略
普朗克鑽研黑體幅射的問題多年,想從理論上找一個理論來完全解釋其頻譜與溫度的關係
Eisbrg & Resnic 量子物理教科書的第二版提到,在 1900 年普朗克提出一個分佈來同時符合 "插值,interpolate" 高頻時的 Wein 公式及低頻時的 Rayleigh-Jeans 公式。(但同一教科書的第三版又選擇不去介紹這些細節。)
亦參見 維基百科 Planck's law
以下是他著名的 (正確的) 光譜能量密度公式
其想法如下:
他含蓄而保留地引入 "熱(電磁)幅射的能量" 是量子化的觀念,如此導致:
(0) 如果振子能量連續,依古典理論之結果,平均能量恰為 kT
(1) 如果振子能量不連續,但 Δε << kT,平均能量仍接近 kT
(2) 如果振子能量不連續,但 Δε ~ kT,平均能量小於 kT
(3) 如果振子能量不連續,但 Δε >> kT,平均能量 << kT
上述結果的圖像見下列圖示:
注意到上面 (1) 與 (3) 的情況,為因應低頻與高頻的能譜結果,普朗克兩種都需要(即他想要低頻振子不連續級距小,高頻振子不連續級距大),他因此假設
故令
考量能量不連續且每個能量單位(量子)是正比於幅射駐波頻率的情況下,按波玆曼分佈重新去平均能量的結果(過程見 p0、p1)得
請注意,普朗克並未改變古典物之所建立的波玆曼分佈,它只是要求單一電磁駐波模式的能量大小不是連續而是離散的。具體地說,古典物理的框架下與振子能量有關的因素之一是振幅,振幅越大,則能量越高。至於振幅變化的形式與範圍,則是連續的大小。因此,在溫度為 T 時的幅射能量密度是
他透過與實驗光譜比對得得到 h 值
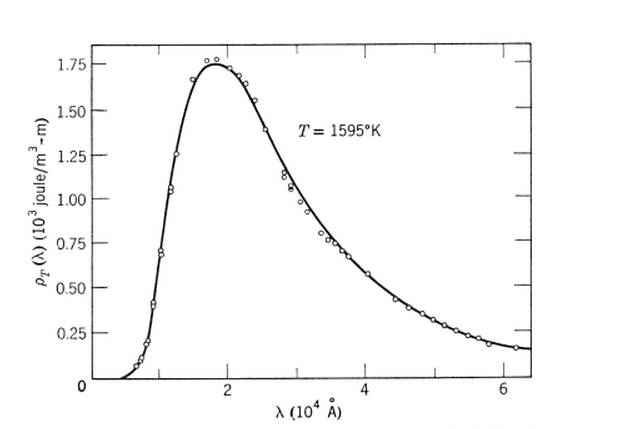
如此與實驗結果比較,不管是低頻、中頻或高頻,都符合得近乎完美。
光電效應
光電效應的實驗
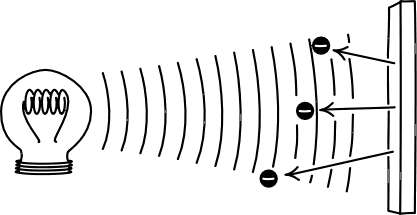
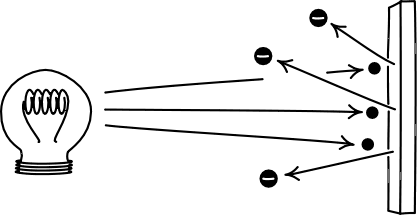
光照金屬板,在適當的情況會有電子跳出表面,叫作光電子。古典理論的不足
有無光電子的逼出,是取決於光照的顏色(即波長、頻率),而不是它的亮度。
波的能量在振幅而非頻率
愛因斯坦的解釋
愛因斯坦提出光的粒子說 "光子"
而光子的能量是 E = hv
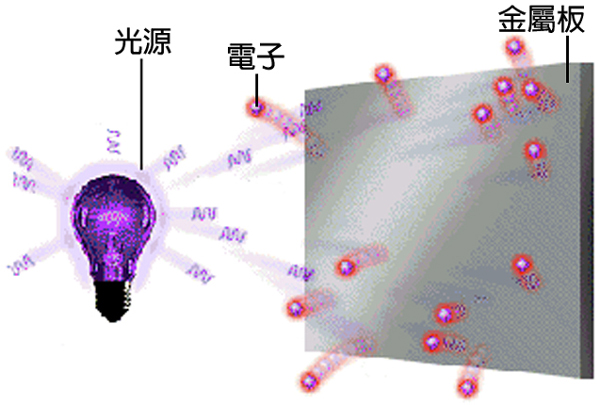
以下是淡江大學自編教材裏的一張圖
回來看普朗克提出電磁波能量不連續的問題
電磁波是光子,它本來就是一顆一顆的,也難怪在考慮 "振子" 的振幅時,怎麼會有不連續的振幅這種事情。然而,光也有波勳現象,馬克斯威爾方程式明白寫著光是波,這麼樣的物理公式或數學表法才能同時把這兩個特性描述出來?
另外,一個由此引發的問題就是,是只有電磁波(光子)才是振幅能量量子化的,還是說其他的波也是沒有連續振幅而是離散振幅?簡單地問,電磁波是粒子,其他所有波都是粒子嗎?(這個答案的
事實上,除了熱蝠射這朵烏雲之外,另有一個物理問題也面臨困境,等著量子概念的解救,那就是原子結構的問題。
原子光譜
不同元素其燃燒的火焰不同(節慶煙火),如何解釋
利用光波干涉效應的光柵分光儀,可針對光譜作精密的分析
原子的模型
拉塞福-核桃而非西瓜
為何原子是穩定的?
波爾模型與原子光譜


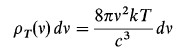
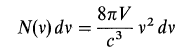
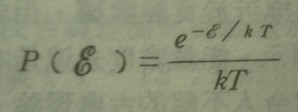
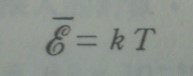
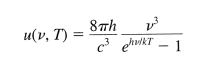
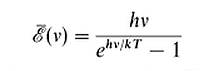
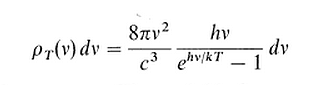

No comments:
Post a Comment