| 近代物理 標題:有關於波函數的單位因次問題 |
 1:李璿榮譽點數28點(大學理工科系)張貼:2011-04-28 17:56:03:來自 國立中山大學 1:李璿榮譽點數28點(大學理工科系)張貼:2011-04-28 17:56:03:來自 國立中山大學 |
在量子物理裡,我們表示一個波函數的歸一化如下式所表示
 從這個式子裡我們可以知道波函數的因次是長度因次的負二分之一次方。因為一維波函數的絕對值平方對 dx 整個一維空間作積分會等於 1 。 1 代表在整個空間裡發現粒子的機率,積率是沒有因次單位的,而 dx 的因次單位為長度的單位,故得知波函數的因次單位就是長度的 -1/2 次方。 從這個式子裡我們可以知道波函數的因次是長度因次的負二分之一次方。因為一維波函數的絕對值平方對 dx 整個一維空間作積分會等於 1 。 1 代表在整個空間裡發現粒子的機率,積率是沒有因次單位的,而 dx 的因次單位為長度的單位,故得知波函數的因次單位就是長度的 -1/2 次方。
而根據展開理論我們得知波函數可以以一個選定的 eigenstates 做線性展開,例如我以 Hamiltonian 的 eigenstates 做線性展開可得
 然後再以這些 Un(x) 作為 configuration space 的廣義坐標軸,我們就可以用矩陣來表示波函數,波函數就會變成一個在這個 configuration space 裡的向量 然後再以這些 Un(x) 作為 configuration space 的廣義坐標軸,我們就可以用矩陣來表示波函數,波函數就會變成一個在這個 configuration space 裡的向量
如:


而波函數的歸一化可以這樣表示

但是當我檢查單位因次時發現,兩個波函數向量內積等於1可以得知它們是沒有單位因次的,而波函數的單位因次是長度的-1/2次方。當一個函數以向量來表示時它的單位因次會發生改變嗎?沒有這種事吧,可是我又一直想不出這個矛盾的盲點到底在什麼地方,可以請教教授您我的問題出在哪裡嗎?在此先謝謝教授。
(PS.不知怎麼回事我不能使用數學方程式編輯器編輯式子,我最後只能使用貼圖的笨方法來處理,這樣占用網路空間實在很抱歉。)
[ 這篇文章被編輯過: 李璿 在 2011-04-28 18:06:58 ] |
 2:Hydrogen Dioxide (研究所)張貼:2011-04-28 18:43:41:地點*台灣高雄 [回應上一篇] 2:Hydrogen Dioxide (研究所)張貼:2011-04-28 18:43:41:地點*台灣高雄 [回應上一篇] |
波函數理面藏了一個歸一化常數, 此常數平方後的單位可以和你之前說的「長度的-1/2次方」消掉最後變成無因次.
你忘記考慮歸一常數了!!!
等等...
說錯了, 由量子力學的基本假設: 在全空間找到特定粒子的總機率是1.
因此 量子力學假設 <phi x| phi x> =1 而由Dirac符號的定義, 所以對位置 由負無限大到正無限大積分後的結果是1
由此假設與積分結果是一 我們可以將一特定物理系統(如 簡諧振子或無限位能井)由其「邊界條件」解出波函數 (如無限井 phi (x ) = A sqrt (2/L) ) 由歸一化假設 反解出A 然後再餵回去phi(x)
這個A就是前面說的規一化常數. 把phi(x)代回假設則能讓 <phi (x) | phi(x)>=1 (如果不是1則是錯誤的)
|
 3:黃福坤(研究所)張貼:2011-04-28 20:49:06:地點 台灣台北 [回應第1篇] 3:黃福坤(研究所)張貼:2011-04-28 20:49:06:地點 台灣台北 [回應第1篇] |

想一想 以上等式都 成立嗎? 區分 意義相同 與等號的差異
|
 4:李璿榮譽點數28點(大學理工科系)張貼:2011-04-28 23:03:03:來自 國立中山大學 [回應上一篇] 4:李璿榮譽點數28點(大學理工科系)張貼:2011-04-28 23:03:03:來自 國立中山大學 [回應上一篇] |
To : Hydrogen
你所說的 ψ(x) = A sqrt (2/L) 應該指得是在無線位能井裡粒子它的 Hamiltonian 的 eigenstate un(x) 吧。它的確是有一個歸一化係數包含在 un(x) ,使得這個 eigenstate 也能夠歸一化。然後 ψ(x) 會等於這些 un(x) 的線性組合。而個別的 un(x) 前面都會乘上一個 Cn ,而這個 Cn 也是歸一化係數。我們可以藉由正交的特性求出它們。
To:黃教授
就我目前的瞭解以及能確定的是
1.
 這個式子是成立的,因為這是Dirac notation的定義,而兩個波函數做這樣的運算所要表達的就是它的歸一化。 這個式子是成立的,因為這是Dirac notation的定義,而兩個波函數做這樣的運算所要表達的就是它的歸一化。
2.
 我想這個也是成立的,因為兩個向量矩陣內積後的代數運算結果會跟第一個式子的運算結果是一樣的。 我想這個也是成立的,因為兩個向量矩陣內積後的代數運算結果會跟第一個式子的運算結果是一樣的。
因此問題可能出在於這兩個式子不能用等號把他們連結在一起吧!因為一個是函數的積分運算,一個是矩陣的代數運算,但是這兩個式子的運算結果會是一樣的(不考慮單位因次)。但是當我嘗試著去驗算單位因次時,我就實在不知道該怎麼去做解釋。
另外我想在問教授一個問題。若我想要用矩陣來表是一個向量,則這個矩陣所表示的向量它的單位因次會是?舉個例子,力是向量,則它會有三個分量,分別是x方向的、y方向的和z方向的。若我想以矩陣表示力這個向量會變成一個3x1矩陣。那這個向量矩陣的單位會是力的單位嗎?還是這個矩正可以是無單位因次的,力的單位因次就把它放到三個空間的單位向量裡,而單位向量不出現在矩陣裡,所以這個矩陣就變成了無單位因次?可以這樣做嗎?
[ 這篇文章被編輯過: 李璿 在 2011-04-28 23:23:37 ] |
 5:Hydrogen Dioxide (研究所)張貼:2011-04-29 02:06:22:地點*台灣高雄 [回應上一篇] 5:Hydrogen Dioxide (研究所)張貼:2011-04-29 02:06:22:地點*台灣高雄 [回應上一篇] |
李同學, 我覺得你第二那個部分的波函數取向量符號, 有點奇怪. 在量子力學中, 運算元可以放上向量符號, 如  --> -->  是合法的. 但是你上面寫的phi*phi有點奇怪. 是合法的. 但是你上面寫的phi*phi有點奇怪.
Quote:
|

|
|
Quote:
|
在 2011-04-28 23:03:03, 李璿 寫了:
To : Hydrogen
你所說的 ψ(x) = A sqrt (2/L) 應該指得是在無線位能井裡粒子它的 Hamiltonian 的 eigenstate un(x) 吧。它的確是有一個歸一化係數包含在 un(x) ,使得這個 eigenstate 也能夠歸一化。然後 ψ(x) 會等於這些 un(x) 的線性組合。而個別的 un(x) 前面都會乘上一個 Cn ,而這個 Cn 也是歸一化係數。我們可以藉由正交的特性求出它們。
|
|
我說的ψ(x) = A sqrt (2/L)的確是infinite potential well的特徵函數(我第二格回應已經有說). 你們大學生或者正在學量子力學的人,要十分的小心, 也就是念書的每一步要知道自己在做甚麼. 偽何要解出這個特徵函數, 是因為薛丁格方程式 H | phi > = E|phi> 由其數學特性,|phi>的解有無限多個, 我們必須要利用邊界條件來讓解的形式固定下來. 也就是說我們要獲得一個特定的解.
我剛看了一下,你這段話有點問題..
「你所說的 ψ(x) = A sqrt (2/L) 應該指得是在無線位能井裡粒子它的 Hamiltonian 的 eigenstate un(x) 吧。它的確是有一個歸一化係數包含在 un(x) ,使得這個 eigenstate 也能夠歸一化。然後 ψ(x) 會等於這些 un(x) 的線性組合。」
由於時間的關係 (限在是深夜, 時間太晚了 已經熬夜了)
明後天再看看,若 有空我再來跟你討論.
|
 6:Hydrogen Dioxide (研究所)張貼:2011-04-29 18:04:17:地點*台灣高雄 [回應第3篇] 6:Hydrogen Dioxide (研究所)張貼:2011-04-29 18:04:17:地點*台灣高雄 [回應第3篇] |
Quote:
|
在 2011-04-28 20:49:06, 黃福坤 寫了: 
想一想 以上等式都 成立嗎? 區分 意義相同 與等號的差異
因為cn那個是無窮多維的空間 , 是寫成級數的. 也就是一個一個向量彼此的分量內積,然後全部加起來 等於1
|
|
等式左邊為找到粒子的總機率為1的一般性表示法,是對全空間(嚴格來說是對x,y,z)做積分, 而另外一邊的表示法若跟此等式畫成等號,會有問題. |
 7:李璿榮譽點數28點(大學理工科系)張貼:2011-05-01 14:10:51:來自 國立中山大學 [回應上一篇] 7:李璿榮譽點數28點(大學理工科系)張貼:2011-05-01 14:10:51:來自 國立中山大學 [回應上一篇] |
|
最近我在查了Stephen Gasiorowicz所寫的量子物理第三版第6-1節的地方,我發現我搞錯了一件事。
|ψ〉所要表達的是波函數以向量來表示時的代表符號,因此我之前這樣寫|ψ(x)〉是不對的表示方式。ψ(x)是函數,而|ψ〉是向量,而〈ψ|ψ〉會等於
純粹只是數值上它們會相等而以(波函數是要對三度空間積分沒錯,只是在這裡我想為方便討論先看一維就好),而〈ψ|ψ〉它實際上是要等於兩個波函數向量的代表矩陣的乘積。所以我之前把Dirac notation的定義搞錯了。
所以我修改一下我在第四篇回應的部分
[quote] 在 2011-04-28 23:03:03, 李璿 寫了:
1.
 這個式子是成立的,因為這是Dirac notation的定義,而兩個波函數做這樣的運算所要表達的就是它的歸一化。 這個式子是成立的,因為這是Dirac notation的定義,而兩個波函數做這樣的運算所要表達的就是它的歸一化。
不對。要把〈ψ(x)|ψ(x)〉給去掉,而且正確的表示應該是〈ψ|ψ〉,上式的式子只是在數值上它們會相等,而意義上是不一樣的。
2.

我想這個也是成立的,因為兩個向量矩陣內積後的代數運算結果會跟第一個式子的運算結果是一樣的。
把兩個波函數上面標上向量符號內積的部分改成〈ψ|ψ〉,這樣才對。
[ 這篇文章被編輯過: 李璿 在 2011-05-01 14:12:11 ] |
 8:Hydrogen Dioxide (研究所)張貼:2011-05-01 16:16:01:地點*台灣台北 [回應上一篇] 8:Hydrogen Dioxide (研究所)張貼:2011-05-01 16:16:01:地點*台灣台北 [回應上一篇] |
http://zh.wikipedia.org/wiki/%E6%AD%A3%E4%BA%A4%E5%87%BD%E6%95%B0
對於兩個函數f 和g,可以定義如下的內積:
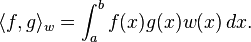
這裡引進一個非負的權函數w(x)。這個內積叫做帶權w(x)的內積。
------------------------------------------------------------------------------------
我記得這個函數的內積, Arfken物理數學有提到, 所以就你的例子來說, <phi (x) | phi (x)> 的積分表達式那個,並沒有錯誤.
「最近我在查了Stephen Gasiorowicz所寫的量子物理第三版第6-1節的地方,我發現我搞錯了一件事。」
就我看過的Shankar量子力學, 你以下所寫的並沒有錯誤
-----------------------------------------------------------------------------------
1.

這個式子是成立的,因為這是Dirac notation的定義,而兩個波函數做這樣的運算所要表達的就是它的歸一化。
不對。要把〈ψ(x)|ψ(x)〉給去掉,而且正確的表示應該是〈ψ|ψ〉,上式的式子只是在數值上它們會相等,而意義上是不一樣的。
----------------------------------------------------------------------------------
〈ψ(x)|ψ(x)〉= ( <x|ψ> )* <x|ψ> = <ψ|x> <x|ψ> =〈ψ|I ψ〉=〈ψ|ψ〉
其中 |x> <x| =Idendity (對角線元素 全部是1)
|ψ(x) > 的意義是波函數ψ(狀態向量(state vector))投影到x基底 並標寫成右向量
而把這個符號寫成左向量的形式 只是該右向量取共軛再轉置.
|
 9:黃福坤(研究所)張貼:2011-05-01 23:26:23:地點 台灣台北 [回應第4篇] 9:黃福坤(研究所)張貼:2011-05-01 23:26:23:地點 台灣台北 [回應第4篇] |
(3,5) 是向量的一種表示式
這個向量 可能代表 位移/速度或加速度 或任何形式為向量的 物理量
這個數學的向量表示式 有單位嗎?
想一想 矩陣是否類似!
|
 10:李璿榮譽點數28點(大學理工科系)張貼:2011-05-04 16:36:37:來自 國立中山大學 [回應上一篇] 10:李璿榮譽點數28點(大學理工科系)張貼:2011-05-04 16:36:37:來自 國立中山大學 [回應上一篇] |
我想先說明一下我對函數跟向量的看法好了。
假設現在有一個速度跟時間的函數 V(t) ,並且我假設 V(t)=3t2+5t+1( 純粹假設 )
我會習慣去分析它的因次。例如在 3t2 這一項,我會認為 t2 的因次為秒,而 t2 前面的係數 3 的因次就是公尺 / 秒 3 。在 5t 這一項我會認為 t 前面的係數因次是公尺 / 秒 2 。而最後面的常數項因次是公尺 / 秒 。所以這三項整個加起來它的因次都會是速度的因次。 ( 不會有物理量是由不同因次的物理量相加而得到的 )
再來描述我對向量的看法。一樣我舉個例子。例如力的向量 \vec{F}=Fx\hat{i} + Fy\hat{j} + Fz\hat{k}
其中  、 、  、 、  分別代表直角做標的三個座標軸的單位向量,它是 dimensionless ,而 Fx 、 Fy 、 Fz ,這三個單位向量前的係數是有單位因次的,都是牛頓 ( 我用 SI 單位制來看 ) 分別代表直角做標的三個座標軸的單位向量,它是 dimensionless ,而 Fx 、 Fy 、 Fz ,這三個單位向量前的係數是有單位因次的,都是牛頓 ( 我用 SI 單位制來看 )
因此若是用矩陣來表示這個向量的話會是 F=\left[\array{Fx \\ Fy \\ Fz}] \right
而這個矩陣是有單位因次的,也就是這些元素的單位因次,所以單位因次為牛頓。 ( 我的想法是整個矩陣的單位因次就是矩陣裡的元素的因次,例如角動量 operator 裡的每個元素就一定會有公因數為 h/2π 的常數在,它提供了角動量的單位 )
另外我之前一直有一個想法一個物理量改成以向量來表示的話並沒有理由它的因次會發生改變。例如速度只考慮大小的話它的單位因次就是公尺 \ 秒,當你加上向量符號或是以矩陣來表示時它的單位沒有理由改變。
但是當我把這個概念用在函數的內積上就會產生問題。例如現在我有兩個函數 f(x) 和 g(x) 它們在區間 [a,b] 是有意義的,而兩個函數的內積標示為<f,g> = math_failure (math_unknown_error\f): \int_a^b \f(x)g(x)dx ( 在此令 weight function 為 1 ,不考慮權重 ) 。我就會發現多一個 dx 的因次 ( 也就是積分的結果比起在傳統上我們處理在空間裡兩個向量內積後的因次是將兩個向量的因次直接相乘多了長度一個因次 ) 。
我想問題可能是出在我太過受限於空間座標裡兩個向量的內積定義了。兩個函數可以當成在某個 vector space 裡的兩個向量。而兩個代表函數的向量其內積就定義為兩個函數相成後再對 dx 做積分。因此在 裡 f 是向量, g 是向量,而 就是兩個向量的內積,定義為 math_failure (math_unknown_error\f): \int_a^b \f(x)g(x)dx。
因此我想我上面我說的 一個物理量改成以向量來表示的話並沒有理由它的因次會發生改變 這個概念就有修正的必要。
所以我就直接拿波函數來看好了。
我們先從波函數的歸一化這個式子來看
math_failure (math_unknown_error\r): \int_{-∞}^∞ \ψ*(x)ψ(x)dx
這個式子就跟函數內積的式子像極了,所以我想我也可以表達成〈 ψ*, ψ 〉 =math_failure (math_unknown_error\r): \int \ψ*(x)ψ(x)dx
而在〈 ψ*, ψ 〉這裡 ψ 表示的不是函數,而是已經當成向量了。
而 ψ 其實我們用 ket 來表示這個向量的話應該寫成 ψ 〉
而根據 expansion theory 可以得知波函數可以以任何 operator 的 eigenstates 作線性展開,也就是
ψ(x)=sum_{i=1} \Cnun(x)
而其中個別的 un(x) 就把它以向量來表示,並且同時去掉它的單位讓它變成無因次 ( 我其實不是很瞭解是否可以這樣做,只是若要解釋我之前的問題的話,我覺得必須得如此定義 ) ,而且我們把 un(x) 做為單位向量讓它 span 出一個 vector space ,然後再以矩陣表示 ψ(x)= \left[\array{C1 \\ C2 \\ C3 \\ . \\ . \\ .} \right] 這個向量。這樣一來整個波函數在以矩陣表示後就沒有因次了,而且以矩陣表示的波函數再透過相成就表示了兩個向量的內積,而內積的結果會歸一化,也符合了波函數函數內積的定義,結果也是歸一化。
所以〈 ψ|ψ 〉 =math_failure (math_unknown_error\r): \int_{-∞}^∞ \ψ*(x)ψ(x)dx=\left[\array{C*1 & C*2 & C3 & . & . & . } \right] \left[\array{C1 \\ C2 \\ C3 \\ . \\ . \\ .} \right]
以上是我最近整理出來的結果,其實我不是很有把握,但是可以大概解釋我之前的盲點,因此麻煩各位大大和教授看看我這個論點還有什麼地方有問題,在此謝謝。
PS.抱歉我實在不知道我方程式的語法問題出在哪裡,想請問一下教授我該怎麼輸入方程式才會顯示?
[ 這篇文章被編輯過: 李璿 在 2011-05-04 16:56:38 ] |
 11:黃福坤(研究所)張貼:2011-05-04 17:36:48:地點 台灣台北 [回應上一篇] 11:黃福坤(研究所)張貼:2011-05-04 17:36:48:地點 台灣台北 [回應上一篇] |
1.  中 3對應某物理量的數值 該物理量單位可能對應 米/秒3可是3這個數值 僅是數字 中 3對應某物理量的數值 該物理量單位可能對應 米/秒3可是3這個數值 僅是數字
2. 速度  m/s 其向量 m/s 其向量  並沒有單位吧, 以矩陣表示時 每個數值 會有單位嗎? 並沒有單位吧, 以矩陣表示時 每個數值 會有單位嗎?
3, 數學方程式內 必須給正確的TeX指令 ,不可和網頁指令混用 (你有混用 上下標指令,都改用 ^ 或 _ 應該就可成功顯示)
|
 12:李璿榮譽點數28點(大學理工科系)張貼:2011-05-07 15:21:21:地點*台灣台北 [回應上一篇] 12:李璿榮譽點數28點(大學理工科系)張貼:2011-05-07 15:21:21:地點*台灣台北 [回應上一篇] |
那麼我之前所舉的例子
V(t)=3t2+5t+1
這個代表速度的函數本身就會是沒有單位因次了?
所以在這個函數裡t2是dimensionless,它只是代表一個數值,但是他有對應某個單位為秒2物理量,而前面的係數3也是對應某個物理量的數值,它的因次單位是公尺/秒3。
因此對於函數、或是向量而言,其本身都只是個數值。若是我們要對這個數值給予一個定義,譬如說是代表速度、位能、或是電場等等,我們會在這個函數或是向量後面括號再加上代表該物理量的單位因次,並且在分析函數裡每一項自變數的次方數的單位因次以及其前面所帶的常數的因次。
因此波函數本身它只是個函數,而機率密度就是波函數的絕對值平方。我們可以說機率密度這個函數是在空間中某一個位置發現粒子的機率,而其函數本身是沒有單位因次的。但是它是對應於某個物理量因次為1/公尺3在某空間中的數值,而我們稱該物理量為機率密度。
教授請問您是這個意思嗎?
|
 13:黃福坤(研究所)張貼:2011-05-07 22:21:19:地點 台灣台北 [回應上一篇] 13:黃福坤(研究所)張貼:2011-05-07 22:21:19:地點 台灣台北 [回應上一篇] |
從數學角度 函數 數值 或向量 都沒有單位
是結合物理量後 賦予物理量 一個單位
其實 單位對實際可測量的量會有意義

以上數學關係 以物理意義來說 右邊沒有單位
可是 我不會去單獨談  的單位 因為並非可直接測量的量! 的單位 因為並非可直接測量的量!
以波函數 或矩陣 來表示 是兩個不同表徵
兩者涵義相同 但是並非相等
數學函數 積分  可看成是切成很多小段 每一段相加 可看成是切成很多小段 每一段相加
想一想 用矩陣表示時 矩陣的數值還做過歸一化 其作用/目的為何?
|
 14:李璿榮譽點數28點(大學理工科系)張貼:2011-05-08 00:37:00:地點*台灣台北 [回應上一篇] 14:李璿榮譽點數28點(大學理工科系)張貼:2011-05-08 00:37:00:地點*台灣台北 [回應上一篇] |
其實我覺得波函數的歸一化就廣義上來講是指波函數的orthogonality。若兩個函數在所有的物理量算符的運作下,只要有一個算符所對應的eigenvalue對兩個波函數而言是不一樣的話,這兩個波函數就一定會正交。而若是所有物理量的算符所對應的eigenvalue對這兩個波函數而言都是一樣的話那麼這兩個波函數是相同的,而相同的波函數本身是不會正交的。但是我們希望波函數的正交式子是一個實數值,因此我們是拿波函數的complex conjucation和其本身乘積再對空間積分來定義波函數的orthogonality。並且我們在定義波函數其絕對值的平方為機率密度,機率密度對空間積分當然要等於1。
因此我們就有了

這個式子。
而若兩個波函數不一樣的話,那麼其正交性式子所顯現的結果(也就是積分結果)就會是零。
事實上我們可以把函數當成向量來看我們若是把波函數當成向量來看的話,也就是|ψ> 而我們定義它的共厄加轉置為<ψ| 這兩個都是向量,並且我們定義這兩個向量的內積為<ψ|ψ>,而向量可以用矩陣來表示,因此這兩個向量的內積也就是矩陣的相乘, 並且我們已經定義了兩個函數的內積為
現在我們令f(x)為ψ*(x),g(x)為ψ(x),區間[a,b]為負無窮大到正無窮大
這樣子波函數用矩陣表示時,依循內積定義(它的定義就跟兩個函數正交性的式子是一樣的),其運算後的結果就會很自然而然等於1。
而我覺得矩陣的運算比起函數積分運算要來的好處理(很多積分很不好算,或是我根本不會算)。既然用矩陣的表示方法跟我們用的函數的表示方法在意義上是一樣的話,那我們就可以用矩陣來解決量子物理上的問題。另外像是電子的自旋是不能用波函數來描述的,而這時候我們就會用矩陣來代表它的狀態,而運算的結果在含意上就跟我們原先用波函數來處理的結果是一樣的。我想這些就是我們要用矩陣來表示波函數的功用以及目的吧。
[ 這篇文章被編輯過: 李璿 在 2011-05-08 00:53:50 ] |
 (黃福坤)
(黃福坤)




 從這個式子裡我們可以知道波函數的因次是長度因次的負二分之一次方。因為一維波函數的絕對值平方對 dx 整個一維空間作積分會等於 1 。 1 代表在整個空間裡發現粒子的機率,積率是沒有因次單位的,而 dx 的因次單位為長度的單位,故得知波函數的因次單位就是長度的 -1/2 次方。
從這個式子裡我們可以知道波函數的因次是長度因次的負二分之一次方。因為一維波函數的絕對值平方對 dx 整個一維空間作積分會等於 1 。 1 代表在整個空間裡發現粒子的機率,積率是沒有因次單位的,而 dx 的因次單位為長度的單位,故得知波函數的因次單位就是長度的 -1/2 次方。  然後再以這些 Un(x) 作為 configuration space 的廣義坐標軸,我們就可以用矩陣來表示波函數,波函數就會變成一個在這個 configuration space 裡的向量
然後再以這些 Un(x) 作為 configuration space 的廣義坐標軸,我們就可以用矩陣來表示波函數,波函數就會變成一個在這個 configuration space 裡的向量 


 這個式子是成立的,因為這是Dirac notation的定義,而兩個波函數做這樣的運算所要表達的就是它的歸一化。
這個式子是成立的,因為這是Dirac notation的定義,而兩個波函數做這樣的運算所要表達的就是它的歸一化。 我想這個也是成立的,因為兩個向量矩陣內積後的代數運算結果會跟第一個式子的運算結果是一樣的。
我想這個也是成立的,因為兩個向量矩陣內積後的代數運算結果會跟第一個式子的運算結果是一樣的。 -->
-->  是合法的. 但是你上面寫的phi*phi有點奇怪.
是合法的. 但是你上面寫的phi*phi有點奇怪.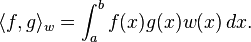
 、
、  、
、  分別代表直角做標的三個座標軸的單位向量,它是 dimensionless ,而 F
分別代表直角做標的三個座標軸的單位向量,它是 dimensionless ,而 F 中 3對應某物理量的數值 該物理量單位可能對應 米/秒
中 3對應某物理量的數值 該物理量單位可能對應 米/秒 m/s 其向量
m/s 其向量  並沒有單位吧, 以矩陣表示時 每個數值 會有單位嗎?
並沒有單位吧, 以矩陣表示時 每個數值 會有單位嗎? 
 的單位 因為並非可直接測量的量!
的單位 因為並非可直接測量的量! 可看成是切成很多小段 每一段相加
可看成是切成很多小段 每一段相加

No comments:
Post a Comment