統計學上的自由度 由于样本中的n个数都是相互独立的，任一個尚未抽出的數都不受已抽出任何数值的影響，所以自由度为n

統計學上的自由度（英语：degree of freedom, df），是指当以样本的统计量（英语：Statistic）来估计总体的参数时，样本中独立或能自由变化的数据的个数，称为该统计量的自由度。
例1：估计总体的平均数（）时，由于样本中的个数都是相互独立的，任一個尚未抽出的數都不受已抽出任何数值的影響，所以c为。
例2：估计总体的方差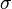（）时所使用的統計量是樣本的方差，而必須用到樣本平均數來計算。在抽樣完成後已確定，所以大小為的樣本中只要个数确定了，第個數就只有一個能使樣本符合的數值。也就是說，樣本中只有個數可以自由變化，只要確定了這個數，方差也就确定了。这裡，平均數就相当于一个限制条件，由于加了这个限制条件，樣本方差的自由度为。
例3：统计模型的自由度等于可自由取值的自变量（英语：Dependent and independent variables）的个数。如在回归方程中，如果共有个参数需要估计，则其中包括了个自变量（与截距对应的自变量是常量）。因此该回归方程的自由度为。
例4：如果用刀剖柚子，在北极点沿经线方向割3刀，得6个角。这6个角可视为3对。6个角的平均角度一定是60度。其中半边3个角中，只会有2个可以自由选择，一旦2个数值确定第3个角也会唯一地确定。在总和已知的情况下，切分角的个数比能够自由切分的个数大1。