Wednesday, August 15, 2012

帶電粒子運動軌道的電荷密度可以用狄拉克δ函數表達為

帶電粒子運動軌道的電荷密度可以用狄拉克δ函數表達為

這是黎納-維謝純量勢乘以雅可比行列式因子 \mathfrak{J}\,\! 。追根究柢，原因是移動中的帶電粒子，雖然理論上是點粒子，但是由於它是在移動中，在積分裏所佔有的體積顯得比較大，所帶的電荷因此比較多，所以產生的電勢不同

黎納-維謝勢
维基百科，自由的百科全书
跳转到： 导航、 搜索
在這篇文章內，向量與标量分別用粗體與斜體顯示。例如，位置向量通常用 \mathbf{r}\,\! 表示；而其大小則用 r\,\! 來表示。檢驗變數或場變數的標記的後面沒有單撇號「'\,\!」；源變數的標記的後面有單撇號「'\,\!」。
跳过字词转换说明
艾密·維謝
在電動力學裏，黎納-維謝勢指的是移動中的帶電粒子的推遲勢。從馬克士威方程組，可以推導出黎納-維謝勢；而從黎納-維謝勢，又可以推導出一個移動中的帶電粒子所生成的含時電磁場。但是，黎納-維謝勢不能描述微觀系統的量子行為。
阿弗雷-瑪麗·黎納（英语：Alfred-Marie Liénard） 於 1898 年，艾密·維謝（英语：Emil Wiechert）於1900年，分別獨立地研究求得黎納-維謝勢的公式[1][2]。於 1995 年, Ribarič 和 Šušteršič 正確計算出移動中的偶極子和四極子（英语：quadrupole）的推遲勢[3]。

目录

[隐藏]

[编辑] 歷史重要性

經典電動力學的研究，關鍵地助導阿爾伯特·愛因斯坦發展出相對論。愛因斯坦細心地分析黎納-維謝勢和電磁波傳播，所累積的心得，引領他想出在狹義相對論裏對於時間和空間的概念。經典電動力學表述是一個重要的發射台，使得物理學家能夠飛航至更複雜的相對論性粒子運動的學術領域。
雖然經典電動力學表述的黎納-維謝勢，可以很準確地描述，獨立移動中的帶電粒子的物理行為，但是在原子層次，這表述遭到嚴峻的考驗，無法給出正確地答案。為此緣故，物理學家感到異常困惑，因而引發了量子力學的創立
對於粒子發射電磁輻射的能力，量子力學又添加了許多新限制。經典電動力學表述，表達於黎納-維謝勢的方程式，明顯地違背了實驗觀測到的現象。例如，經典電動力學表述所預測的，環繞著原子不停運動的電子，由於連續不斷地呈加速度狀態，應該會不停地發射電磁輻射；但是，實際實驗觀測到的現象是，穩定的原子不會發射任何電磁輻射。經過日以繼夜，廢寢忘食的研究論證，物理學家發現，電磁輻射的發射完全是由電子軌域的離散能級的躍遷所控制（參閱波耳原子）。在二十世紀後期，經過多年的改進與突破，量子電動力學成功地解釋了帶電粒子的放射行為。

[编辑] 物理理論

帶電粒子的移動軌道。
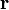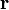假設，從源頭位置 \mathbf{r}'\,\! 往檢驗位置 \mathbf{r}\,\! 發射出一束電磁波，而這束電磁波在檢驗時間 t\,\! 抵達觀測者的檢驗位置 \mathbf{r}\,\! ，則這束電磁波發射的時間是推遲時間 t_r\,\! 。由於電磁波傳播於真空的速度是有限的，觀測者檢驗到電磁波的檢驗時間 t\,\! ，會不同於這電磁波發射的推遲時間 t_r\,\! 。推遲時間 t_r\,\! 定義為檢驗時間 t\,\! 減去電磁波傳播的時間：
t_r\ \stackrel{def}{=}\ t - \frac{|\mathbf{r} - \mathbf{r}'|}{c}\,\! ；
其中，c\,\! 是光速。
推遲時間的概念意味著電磁波的傳播不是瞬時的。電磁波從發射位置傳播到終點位置，需要一段傳播期間，稱為時間延遲。與日常生活的速度來比，電磁波傳播的速度相當快。因此，對於小尺寸系統，這時間延遲，通常很難察覺。例如，從開啟電燈泡到這電燈泡的光波抵達到觀測者的雙眼，所經過的時間延遲，只有幾兆分之一秒。但是，對於大尺寸系統，像太陽照射陽光到地球，時間延遲大約為 8 分鐘，可以經過實驗偵測察覺。

[编辑] 表達方程式

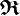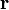假設，一個移動中的帶電粒子 ，所帶電荷為 q\,\! ，隨著時間 t\,\! 而改變的運動軌道為 \mathbf{w}(t)\,\!。設定向量 \boldsymbol{\mathfrak{R}}\,\! 為從帶電粒子位置 \mathbf{r}'=\mathbf{w}(t)\,\! 到檢驗位置 \mathbf{r}\,\! 的分離向量：
\boldsymbol{\mathfrak{R}}=\mathbf{r} - \mathbf{r}'=\mathbf{r} - \mathbf{w}(t)\,\! 。
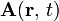則黎納-維謝純量勢 \Phi(\mathbf{r},\,t)\,\! 和黎納-維謝向量勢 \mathbf{A}(\mathbf{r},\,t)\,\! 分別以方程式表達為
\Phi(\mathbf{r},\,t) = \frac{1}{4\pi\epsilon_0}\ \frac{q c}{\mathfrak{R} c - \boldsymbol{\mathfrak{R}}\cdot \mathbf{v}}\,\! 、
\mathbf{A}(\mathbf{r},\,t) =\frac{\mathbf{v}}{c^2}\Phi(\mathbf{r},\,t) \,\! ；
其中，\epsilon_0\,\! 是真空電容率，\mathbf{v}\,\! 是帶電粒子的移動速度， \mathbf{v}(t)=\frac{d\mathbf{w}}{dt}\,\! 。
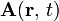雖然黎納-維謝純量勢 \Phi(\mathbf{r},\,t)\,\! 和黎納-維謝向量勢 \mathbf{A}(\mathbf{r},\,t)\,\! 的時間參數是 t\,\! ，方程式右手邊的幾個變數，帶電粒子位置 \mathbf{r}'\,\! 和速度 \mathbf{v}\,\! 都是採推遲時間 t_r\,\! 時的數值：
\mathbf{r}'=\mathbf{w}(t_r)\,\! 、
\mathbf{v}=\mathbf{v}(t_r)\,\! 。

[编辑] 推導

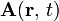從推遲勢，可以推導出黎納-維謝勢。推遲純量勢 \Phi(\mathbf{r},\,t)\,\! 與推遲向量勢 \mathbf{A}(\mathbf{r},\,t)\,\! 分別以方程式定義為（參閱推遲勢）
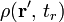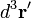\Phi(\mathbf{r},\,t)\ \stackrel{def}{=}\ \frac{1}{4\pi\epsilon_0}\int_{\mathcal{V}'} \frac{\rho(\mathbf{r}' ,\, t_r)}{\mathfrak{R}}\, d^3\mathbf{r}'\,\! 、
\mathbf{A}(\mathbf{r},\,t)\ \stackrel{def}{=}\ \frac{\mu_0}{4\pi}\int_{\mathcal{V}'} \frac{\mathbf{J}(\mathbf{r}',\,t_r)}{\mathfrak{R}}\, d^3\mathbf{r}'\,\! ；
其中，\rho(\mathbf{r}' ,\, t_r)\,\! 是電荷密度，\mathbf{J}(\mathbf{r}',\,t_r)\,\! 是電流密度，\mathcal{V}'\,\! 是積分的體空間，d^3\mathbf{r}'\,\! 是微小體元素，\mathfrak{R}\,\! 向量還是採推遲時間 t_r\,\! 時的數值。
帶電粒子運動軌道的電荷密度可以用狄拉克δ函數表達為
\rho(\mathbf{r},\,t)=q\delta(\mathbf{r} - \mathbf{w}(t))\,\! ；
其中，\delta(\mathbf{r} - \mathbf{w}(t))\,\! 是狄拉克δ函數。
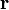代入推遲純量勢 \Phi(\mathbf{r},\,t)\,\! 的方程式，
\Phi(\mathbf{r},\,t)=\frac{q}{4\pi\epsilon_0}\int_{\mathcal{V}'} \frac{\delta(\mathbf{r}' - \mathbf{w}(t_r))}{\mathfrak{R}}\, d^3\mathbf{r}'\,\! 。
由於狄拉克δ函數 \delta(\mathbf{r}' - \mathbf{w}(t_r))\,\! 的積分會從 \mathbf{r}'\,\! 的可能值中，挑選出當 \mathbf{r}'=\mathbf{w}(t_r)\,\! 時，所有變數的數值。所以，在積分內的變數，都可以被提出積分，採推遲時間 \mathbf{r}'=\mathbf{w}(t_r)\,\! 時所計算出的數值。積分內，只剩下狄拉克δ函數等待進一步處理：
\Phi(\mathbf{r},\,t)=\frac{q}{4\pi\epsilon_0\mathfrak{R}}\int_{\mathcal{V}'} \delta(\mathbf{r}' - \mathbf{w}(t_r))\, d^3\mathbf{r}'\,\! 。
由於推遲時間 t_r\,\! 相依於三個變數 t\,\! 、\mathbf{r}\,\! 、\mathbf{r}'\,\! ，這積分比較難計算，需要使用換元積分法[4]。設定變數 \boldsymbol{\eta}=\mathbf{r}' - \mathbf{w}(t_r)\,\! 。那麼，其雅可比行列式 \mathfrak{J}\,\! 為
\mathfrak{J}=\cfrac{\partial \boldsymbol{\eta}}{\partial \mathbf{r}'} =\begin{vmatrix} \cfrac{\partial \eta_x}{\partial x'} & \cfrac{\partial \eta_x}{\partial y'} & \cfrac{\partial \eta_x}{\partial z'} \\ \cfrac{\partial \eta_y}{\partial x'} & \cfrac{\partial \eta_y}{\partial y'} & \cfrac{\partial \eta_y}{\partial z'} \\ \cfrac{\partial \eta_z}{\partial x'} & \cfrac{\partial \eta_z}{\partial y'} & \cfrac{\partial \eta_z}{\partial z'} \\ \end{vmatrix}\,\!。
行列式內分量很容易計算，例如：
\cfrac{\partial \eta_x}{\partial x'}=1 - \cfrac{\partial w_x}{\partial x'}=1 - \cfrac{\partial w_x}{\partial t_r}\ \cfrac{\partial t_r}{\partial x'}=1 - v_x\cfrac{\partial t_r}{\partial x'}\,\! 、
\cfrac{\partial \eta_y}{\partial x'}=\cfrac{\partial w_y}{\partial x'}=\cfrac{\partial w_y}{\partial t_r}\ \cfrac{\partial t_r}{\partial x'}=v_y\cfrac{\partial t_r}{\partial x'}\,\! 。
按照上述方法，經過一番計算，可以得到
\mathfrak{J}=1 - \mathbf{v}\cdot\nabla' t_r= 1 - \hat{\boldsymbol{\mathfrak{R}}}\cdot\mathbf{v}/c\,\! 。
所以，推遲純量勢 \Phi(\mathbf{r},\,t)\,\! 的方程式變為
\Phi(\mathbf{r},\,t)=\frac{q}{4\pi\epsilon_0\mathfrak{R}}\int_{\mathcal{V}'} \delta(\boldsymbol{\eta})\cfrac{\partial \mathbf{r}'}{\partial \boldsymbol{\eta}}\, d^3\boldsymbol{\eta} =\frac{q}{4\pi\epsilon_0\mathfrak{R}}\int_{\mathcal{V}'} \cfrac{\delta(\boldsymbol{\eta})}{\mathfrak{J}}\, d^3\boldsymbol{\eta} =\frac{q}{4\pi\epsilon_0\mathfrak{R}}\int_{\mathcal{V}'} \cfrac{\delta(\boldsymbol{\eta})}{1 - \hat{\boldsymbol{\mathfrak{R}}}\cdot\mathbf{v}/c}\, d^3\boldsymbol{\eta} \,\! 。
這樣，可以得到黎納-維謝純量勢：
\Phi(\mathbf{r},\,t)= \frac{1}{4\pi\epsilon_0}\ \frac{q c}{\mathfrak{R} c - \boldsymbol{\mathfrak{R}}\cdot \mathbf{v}}\,\! 。
類似地，也可以推導出黎納-維謝向量勢。

[编辑] 物理意義

對於固定不動的帶電粒子，電勢的方程式為
\Phi(\mathbf{r},\,t)= \frac{1}{4\pi\epsilon_0}\ \frac{q}{\mathfrak{R}}\,\! 。
這是黎納-維謝純量勢乘以雅可比行列式因子 \mathfrak{J}\,\! 。追根究柢，原因是移動中的帶電粒子，雖然理論上是點粒子，但是由於它是在移動中，在積分裏所佔有的體積顯得比較大，所帶的電荷因此比較多，所以產生的電勢不同。

[编辑] 移動中的帶電粒子的電磁場

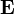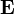從黎納-維謝勢，可以計算電場 \mathbf{E}\,\! 和磁場 \mathbf{B}\,\! ：
\mathbf{E} = - \nabla \Phi - \dfrac {\partial \mathbf{A}} { \partial t } \,\! 、
\mathbf{B} = \nabla \times \mathbf{A}\,\! 。
求得的電場 \mathbf{E}\,\! 和磁場 \mathbf{B}\,\! 分別為[5]
\mathbf{E}(\mathbf{r},\,t)= \frac{q}{4\pi\epsilon_0}\ \cfrac{\mathfrak{R}}{(\boldsymbol{\mathfrak{R}}\cdot \mathbf{u})^3} [(c^2 - v^2)\mathbf{u}+\boldsymbol{\mathfrak{R}}\times(\mathbf{u}\times\mathbf{a})]\,\! 、
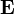\mathbf{B}(\mathbf{r},\,t)= \frac{1}{c}\hat{\boldsymbol{\mathfrak{R}}}\times\mathbf{E}(\mathbf{r},\,t)\,\! ;
其中，向量 \mathbf{u}\,\! 設定為 c\hat{\boldsymbol{\mathfrak{R}}} - \mathbf{v}\,\! ，帶電粒子的加速度是 \mathbf{a}=\frac{d\mathbf{v}}{dt}\,\! 。
檢查電場 \mathbf{E}\,\! 的方程式，右手邊第一個項目稱為廣義庫侖場，又稱為速度場，因為這項目與加速度無關。當 v\ll c\,\! ，粒子速度超小於光速時，\mathbf{u}\to c\hat{\boldsymbol{\mathfrak{R}}}\,\! ，這項目會趨向庫侖方程式：
\mathbf{E} = \frac{q}{4\pi\epsilon_0 }\ \frac{\hat{\boldsymbol{\mathfrak{R}}}}{\mathfrak{R}^2}\,\! 。
右手邊第一個項目稱為輻射場，又稱為加速度場，因為這項目的物理行為主要是由粒子的加速度決定。這個項目能夠描述電磁輻射的生成程序。
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)