點
維基百科,自由的百科全書
(重定向自點)
在幾何學, 拓撲學以及數學的相關分支中, 一個空間中的點用於描述給定空間中一種特別的對象, 在空間中有類似於體積, 面積, 長度, 或其他高維類似物. 一個點是一個零維度對象. 點作為最簡單的幾何概念, 通常作為幾何, 物理, 矢量圖形和其他領域中的最基本的組成部分.
 在歐幾里得幾何中,點是空間中只有位置,沒有大小的圖形。點是整個歐幾里得幾何學的基礎,後者是研究點,線,面,體的一種科學。歐幾里得最初含糊的定義點作為"沒有部分的東西". 在二維歐式空間, 一個點被表示為一個有序對
在歐幾里得幾何中,點是空間中只有位置,沒有大小的圖形。點是整個歐幾里得幾何學的基礎,後者是研究點,線,面,體的一種科學。歐幾里得最初含糊的定義點作為"沒有部分的東西". 在二維歐式空間, 一個點被表示為一個有序對 , 其中第一個數字習慣上表示水平位置,通常記為
, 其中第一個數字習慣上表示水平位置,通常記為 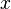 , 第二個數字習慣上表示豎直位置, 通常記為
, 第二個數字習慣上表示豎直位置, 通常記為  . 這一思想很容易廣到三維情況, 此時一個點被表示為一個有序三元組,
. 這一思想很容易廣到三維情況, 此時一個點被表示為一個有序三元組,  , 第三個數字表示高度, 通常記為 z。更加一般的情況下,點被表示為一個有序 n 元組:
, 第三個數字表示高度, 通常記為 z。更加一般的情況下,點被表示為一個有序 n 元組: 其中 n 為點所在的空間的維度.
其中 n 為點所在的空間的維度.
在現代數學語言中,任何集合的元素都叫作「點」,但與三維空間中的點可以沒有任何關係。
儘管點被看做是主要的幾何學和拓撲學中的基本概念, 但是有些幾何和拓撲理論並不需要點的概念. 例如非交換幾何和非點集拓撲. 一個"非點空間"不是作為一個集合來定義的, 而是通過某種類似於幾何上的函數空間的結構(代數上的或者邏輯上的): 連續函數代數或者集合代數.
[編輯] 歐幾里得幾何中的點

二維歐式空間中的有限點集(藍色).
 , 其中第一個數字習慣上表示水平位置,通常記為
, 其中第一個數字習慣上表示水平位置,通常記為 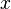 , 第二個數字習慣上表示豎直位置, 通常記為
, 第二個數字習慣上表示豎直位置, 通常記為  . 這一思想很容易廣到三維情況, 此時一個點被表示為一個有序三元組,
. 這一思想很容易廣到三維情況, 此時一個點被表示為一個有序三元組,  , 第三個數字表示高度, 通常記為 z。更加一般的情況下,點被表示為一個有序 n 元組:
, 第三個數字表示高度, 通常記為 z。更加一般的情況下,點被表示為一個有序 n 元組: 其中 n 為點所在的空間的維度.
其中 n 為點所在的空間的維度.在現代數學語言中,任何集合的元素都叫作「點」,但與三維空間中的點可以沒有任何關係。
[編輯] 其他數學分支中的點
在點集拓撲中的點, 定義為一個拓撲空間中的集合的元素.儘管點被看做是主要的幾何學和拓撲學中的基本概念, 但是有些幾何和拓撲理論並不需要點的概念. 例如非交換幾何和非點集拓撲. 一個"非點空間"不是作為一個集合來定義的, 而是通過某種類似於幾何上的函數空間的結構(代數上的或者邏輯上的): 連續函數代數或者集合代數.
No comments:
Post a Comment