相对性效应的关系式却是一个发散型函数，在运用到物理实验过程中却总是出问题。例如，在确定高速运动粒子能量时，总会遇到能量发散的困难，以后虽然用重新定义静止质量的办法，通过“重整化”

物理科学探疑-网友天空-系统观点-李学生-三、Lorentz transformation 的思考

三、Lorentz transformation 的思考

李学生

摘要：本文首先分析了狭义相对论的困难，介绍与Lorentz transformation有关的佯谬。
关键词：狭义相对论、Lorentz transformation、twins paradox、潜水艇悖论、

---

（一）Lorentz transformation的推导

在Einstein著的《狭义与广义相对论浅说》上推导了洛伦兹坐标变换。在推导过程中有这样两个式子:

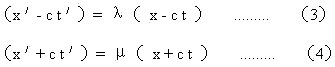
其中（3）式是由:

导出的；而（4）式是由:

导出的；λ和μ是假定的比例常数。

　　我们来分析一下（3）和（4）式的正负号问题。只要时间不为0，由（1）和（2）两式可得:

设S >0，S′>0，而令 x = S，x′= S′，并代入(3)式，得:

由(1)′和(2)′两式可得:

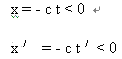
根据前面的假设，故有 x = - S，x′= - S′，并代入(4)式，得:

将上式两边同乘 -1，便有:

由(3)′和 (4)′得出的λ和μ的关系式是:

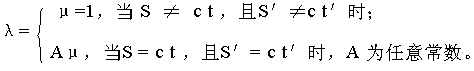
　　假设: a = （λ+μ）/ 2 , b = （λ- μ）/ 2

然后将（3）和（4）两式相加和相减，便得出:

接着便导出:

(引自铁弘先生的《相对论的终结》——探索网站)

（二）狭义相对论的困难

Einstein在1905年《论动体的电动力学》一文中建立狭义相对论时，从洛仑兹变换中推导出了所谓的动钟变慢。我们现在考虑永久放在R系的原点（X=0）上的一个按秒报时的钟（此处的R、r系如上图所示）。T = 0和T = 1对应于该钟接连两声滴嗒。对于这两次滴嗒，洛仑兹变换的第一和第四方程给出

从r去判断，该钟以速度u运动；从这个参考物体去判断，该钟两次滴嗒之间所经过的时间不是１秒，而是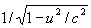秒，亦即比１秒钟长一些。该钟因运动比静止时走的慢了。速度C在这里也具有一种不可达到的极限速度的意义。”

必须指出，相对论的动钟变慢效应是相对的，亦即在相对论中如下表述同样成立：
“我们现在考虑永久放在r系的原点（x=0）上的一个按秒报时的钟。t=0和t=1对应于该钟接连两声滴嗒。对于这两次滴嗒，洛仑兹变换的第一和第四方程给出

从R去判断，该钟以速度u运动；从这个参考物体去判断，该钟两次滴嗒之间所经过的时间不是１秒，而是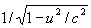秒，亦即比１秒钟长一些。该钟因运动比静止时走的慢了。速度C在这里也具有一种不可达到的极限速度的意义。”

这也就是说，相对论的动钟变慢效应是相对的，即相对运动的观测者都认为对方的时钟慢于自己的时钟慢。（6）

每一个运动着的三维坐标系都有各自独立的一个三维空间度量和一维时间度量，构成四维度量。在同一个坐标系里 ，能量的读数是连续变化的。在相对运动着的不同坐标系里 ，各自的四维度量应该是不同的，这也是因为在相对运动着的不同坐标系里，能量的读数是不同的缘故。然而坐标系主要表现为数学的概念，而能量是客观存在的。为了保证坐标系之间能量特征（包括动能和势能的差值等等）的连续性、一致性，坐标系之间的度量必须建立相应的变换关系。由于光速对所有惯性系不变的要求，描述惯性系（1+3）伪欧氏空间是Minkowski空间，惯性系之间的时空变换，即Minkowski空间中的时空坐标变换只能是Lorentz transformation。如果考虑两空间的时空原点不重合，则它们之间是Poincare transformation. 虽然相对论成功地解释了一些物体高速运动现象，但是它所推出的相对性效应的关系式却是一个发散型函数，在运用到物理实验过程中却总是出问题。例如，在确定高速运动粒子能量时，总会遇到能量发散的困难，以后虽然用重新定义静止质量的办法，通过“重整化”避免了危机，但这种数学形式上的弥补，只是掩盖了表面矛盾，物理实验中的真实矛盾并没有解决，如：量子色动力学(QCD)理论预言，在极端相对论性的原子核碰撞中会产生高温高密夸克－胶子等离子体(QGP),众多国家花大力投入了实验探索。最近却发现理论和实验研究中“还存在着诸多不确定因素”。QGP是否存在还是个问题。相对论性重离子碰撞实验中出现的种种困难，最终归结为：“碰撞中发生了洛仑兹收缩吗？”“如何检验？”70年代提出“惯性约束”，用强激光引发微热核聚变。20多年过去，最近的实验结果是：现有最佳装置的中子产出额远远低于理论估计值。问题竟是：“熵不守恒时相对论性流体力学方程”究竟应该取什么形式？（3）

著名物理学家康特（W. Kantor）剖析60多个实验的第一手资料后有结论：全都基于无效的逻辑或错误的方法。光速问题的争论还将无休止纠缠下去，如不过好三道坎：㈠、电动力学问题与光行差、多普勒效应等一类"纯观察"现象不同，属动力学，因而是无法用狭义相对论来解决的。因此，电动力学的所有实验都不可作为这一"原理"的"验证依据"。史实表明，"质速关系"和"质能关系"等早已在1905年前出现; ㈡、迈克尔逊-莫雷 (1887) 实验只是否定以太论并证实：在光源所在的参照系中光速各向同性总为 c，但不能证实相对于一切惯性系都各向同性总为 c; ㈢、德·西特关于光速与源速无关的著名双星观察论据，有严重的逻辑漏洞，是不可为据的。甚至连大多数的相对论支持者都承认迄今尚未实验观察到Lorentz收缩：“一涉及广延体就出问题……相对论性静力学、热力学、流体力学，至今尚未建立令人满意的理论框架。”由于相对论是在假设光速不变，从时空关系出发推出运动物体相对性效应的，而引起光速不变的真正原因却没有交待。这种从“关系”到“事物”的理论隐藏着严重的缺陷。人们围绕这“光速不变”“Lorentz transformation”展开了激烈的争论。Einstein在解释质能关系上，只承认能量的实在性，却否认物质量的实在性的观点，曾经遭到唯物主义哲学家的尖锐批评。由于相对论所推出的相对性效应以后又陆续被实验观察所证实（尽管对这些实验结果解释还颇有争论）。所以，相对论似乎给人的印象是：它在科学上已经取得了巨大的成功。一部分唯物主义的哲学家开始改变反对相对论的立场，采取实用主义办法：“既然不能把相对论批倒，就得把它纳入自己的框架”，反过来把相对论说成是丰富了辩证唯物主义的时空观、物质观。

（三）与Lorentz transformation有关的佯谬

在科学史上，没有一个理论会象相对论那样产生那么多的“佯谬”，如twins paradox、柔绳佯谬、直角杠杠佯谬、艾伦菲斯特(Ehrenfest) 佯谬、哥德尔 (Godel) 佯谬等。 (3)

在1911年4月波隆哲学大会上，法国物理学家P．朗之万用双生子实验对狭义相对论的时间膨胀效应提出了质疑，设想的实验是这样的：一对双胞胎，一个留在地球上，另一个乘坐火箭到太空旅行。飞行速度接近光速，在太空旅行的双胞胎回到地球时只不过两岁，而他的兄弟早已死去了，因为地球上已经过了200年了。这就是著名的twins paradox。根据狭义相对论，对同一个物理过程，在与其相对静止参照系中测量的时间最短，而在与其有相对运动的参照系中测得的时间将比在物理过程本身进行的参照系内测得的时间（原时）长。那么对于A留地球, B乘坐宇宙飞船出去再回来这个过程，在A看来，在B出去再回来这个过程，他所经历的时间应该比B经历的时间长；而对B来说，在和A分离到再见的过程，他经历的时间应该比A长，这时就无法区分到底谁最更年轻。但我们需要注意到的是，A,B在整个过程中并不都处于相同地位的参照系中，相对于整个宇宙，地球的加速度是比较小的，这里我们忽略这个加速度的影响，而 B从地球到离开，到在回来，需要经过加速离开地球，以一加速度调头返回地球，到达地球后 减速见到A，B处于一个非惯性参照系中，具有加速度，这个是可以真正地“延长”时间的，而A则始终处于地球，一个近似的惯性系中，所以当B返回地球后，B应该比A年轻。或者另外地说，B能够感觉到自己速度的变化，但A感觉不到。可是根据广义相对论的基本原理，物理规律对于任何参考系都成立，对于A而言B不是惯性系，对于B而言A不是惯性系，仍然有矛盾。有人利用广义相对论解释twins paradox，因为在引力场中时钟延缓（加速运动的物体可以产生引力场）；也有人按照Minkowski三角形不等式解释“twins paradox”。1959年James Terrell在《物理评论》杂志上发表论文，指出尺缩效应的形象是人们观测物体上各点对观察者参考系同一时刻的位置构成的形象，常称为“测量形象”。（5）根据相对论的质速关系，实物粒子的全部引力质量随速度的变化而变化，但是在可变的引力质量中又存在着粒子的固有引力质量（或静止引力质量），如何解释两者之间的物理机制呢？ 虽然Lorentz transformation矩阵不包括引力质量，

当运动速度沿X轴时，就化为普通形式。速度引起的引力质量的增加是狭义相对论效应，但是时钟延缓与长度缩短也是狭义相对论效应。

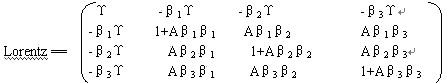
瞬时固有系，是瞬间与质点保持相对静止的惯性系，如果质点的速度不断改变，瞬时固有系也不断替换，它与其质点永远保持相对静止的固有系之间，没有相对速度只有相对加速度。根据狭义相对论在一个质点的瞬时固有系中观察一个质点的运动，不存在狭义相对论效应。笔者认为狭义相对论效应应当为瞬时效应，对于速度不是累积效应。根据场的时空本质的观点，引力质量、时间、空间的狭义相对论效应是同一的。孪生子佯谬的一种版本已被围绕地球在相反方向上飞行的两台精确的钟表的实验所验证。当它们重新相遇时，向东飞行的钟表流逝的时间稍微短一些。（4）

假设在一个惯性参照系中测量一个物体的长度，物体由静止开始加速，直到c/2，然后匀速运动一段距离后开始减速，直到静止。根据Lorentz transformation，物体的长度开始与最后应该相等。可是运动物体的长度缩短，由于物体一直在运动，因此物体最后的长度应该最短，这显然存在着矛盾。在狭义相对论中，物理规律在不同的惯性参照系中是一样的，但物理量在不同的参照系中可能不一样，例如运动物体在其运动方向上的长度将比其静止长度小，可以说是观测效应，因为从测量的含义上去理解，这的确是因为光速不为无穷大（而且任何信息传播速度不得超过光速）的原因，但这也是本质规律，是因为从前面一句话可以看出，这是必然会得出的结论，是规律性的。当开始由静止做加速运动，当速度达到0.99c时开始加速到静止，开始和最后的长度是相等的，因为根据上面的话，运动方向上的动长是和运动相关的，只有它运动，它运动方向的动长才会比静止长度小，如果它运动又静止了，那么它的长度就是静长，当然和原来的相等。设想一个物体先从 静止做加速运动然后做减速运动到静止，在这整个过程里，其运动方向的长度应该是先变小，到速度最大时运动方向动长最小，然后又逐渐变大，最后恢复到静止时长度。 时间变换也符合洛沦兹变换，为什么现代物理学的实验证明（譬如μ子绕地运行）具有累积效应？或许有人认为狭义相对论适用于匀速运动，加速运动应当利用广义相对论解释，可是为何利用原子钟绕地球高速运动（加速运动）时钟减缓，寿命的延长，说明狭义相对论的正确？在长度测量实验中，每时每刻都有速度，长度应当缩短，为何必须用广义相对论呢？因此在μ子和介子实验中，μ子和介子作有加速的圆周运动，实验证实作这样运动的μ子和介子的平均寿命大于静止μ子和介子的平均寿命，并不能说明狭义相对论的正确。如果一个微观粒子作匀速圆周运动，其寿命在延长，但是长度不变，这一点可以用实验验证。直到1959年，特雷尔(j.Terrell)在一篇文章中才指出：不对! 洛仑兹收缩是看不到的。原因很简单：同一时刻从运动物体各点发出的光一般不能同时到达观测者的瞳孔；反之，同时到达瞳孔的光一般也不是同时发出来的。（2）

一个航天飞船以4/5光速从左向右掠过地球。一束光脉冲从座舱的一端发射出并在另一端被反射回来。在地球上的和在航天飞船上的人分别对光进行观察。因为航天飞船的运动，他们在光返回的旅行距离上意见不同。因为按照Einstein关于对所有自由运动的观察者光速相同的假设，他们在光花费多少时间飞行上的意见也应该不同。

“潜水艇悖论”指的是这样一种理论假想情况：首先假设一艘完全浸没在海里的潜水艇，相对于海水静止时能不升不降地正好保持平衡，然后在假设它在与海面平行的方向上以接近光速行进。基于物体的长度在运动方向上收缩的相对论效应，在海面上相对于海水静止的船上的观察者看来，潜水艇本身会收缩，密度会变大，并最终下沉。但潜水艇上的船员们看到的却是飞速向后的海水在收缩，密度在变大，他们会认为：由于海水密度变大后产生浮力变大，潜水艇将上浮。按照相对论，两种互相矛盾的结论都没有错。1989年美国的物理学家萨普利假设海底在特定的参考系中会加速上升，根据广义相对论时空效应而扭曲变形，最终与潜水艇接触，结果看上去是下沉了。最近巴西的物理学家认为，在不同的参考系下，相对于海水静止的观察者和潜水艇员所出的重力场并不相同。他通过严密的数学推理发现，从潜水艇员的角度来看，潜艇以接近光速运动的过程中受到的有效重力，实际上也比潜艇相对于海水静止时大，超过海水密度变大而产生的福利，最终导致潜艇下沉。下面的实验引自涂 润 生先生的《在超严格审查中狭义相对论能过几关？》：

【例1】有甲、乙两个惯例系（也是两种运动状态的两个人），甲认为乙系内的钟慢于甲系内的钟，而乙又认为乙系内的钟快于甲系内的钟。在数学上或逻辑学上看，这是矛盾的。可是相对论的支持者不承认这种矛盾。理由是“没有统一的快慢顺序”，即不同运动状态的观察者对于两只钟的快慢顺序没有统一的认识。两只钟的快慢顺序随观察者的运动状态而变，必然导致“甲、乙两只钟没有统一的快慢顺序”。在无干扰的情况下，观察者改变运动状态，客观存在的两只钟是根据什么物理机制改变快慢顺序的呢？洛伦兹（Lorentz）变换只能描述变化的量而不能阐释变化的物理机制。如果那两只钟是机械钟，那么它们（或它们中的一个）改变走时快慢必须受到变化的力的作用（即时钟快慢改变必须与时钟内部应力或外部力场的改变对应）。观察者改变运动状态所产生的信息一点儿也没有传递到那两只钟上，在这种情况下，钟的快慢仍然变化，需要下列两个条件之一：a钟的快慢变化不需要物理机制；b.唯一的客观实在有非统一的表观结果，用表观的观察结果代替客观实在。有人认为相对论效应全是“影象效应”,但是不能说“已有的实验证实了狭义相对论效应。”

既然找不到未受任何干扰的两只钟改变快慢顺序的机制，就应该认为未受任何干扰的两只钟的快慢顺序不随观察者改变运动状态而改变。这叫做反证法（或排除法），是常用的逻辑方法。

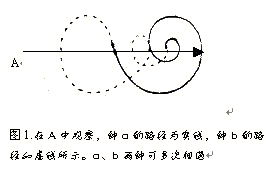
【例2】有A、B两个慢性系，它们各有一只静止的钟（钟a和钟b）。当a和b第一次相遇时，将a和b的读数同时调拨到零，与此同时a和b开始按各自系统中的一条渐开线运动，相对运动的线速度相等。当a和b再次相遇（如图1所示，是办得到的）时，a和b的时间读数中哪个更大？根据相对论可知：在A上观察，b的读数小于a的读数，但在B上观察，b的读数大于a的读数。a、b第一次相遇时读数Ta1和Tb1同时为零是没有争议的，当a、b第二次相遇时，若Ta2=0.20微秒和Tb2=0.21微秒已被B上的观察者观测到了，是完全真实的，那么，由光速与光源的运动速度无关可推知：载有Ta2=0.20μs信息的光信号和载有Tb2=0.21μs信息的光子是同时从a、b第二次相遇的空间点P2上发出的，其他惯性系中的观察者原则上都可同时接收到这两种光信号。换言之，只要光速与光源的运动状态无关，那么，在同一空间点上同时发生的光子（即使它的源的运运状态不同）都能同时到达任何一个观察者的视膜网（这正是双星影象不发生畸变的原因）。可见，在B同时观察到了Ta2=0.20μs、Tb2=0.21μs的前提下，在A上也能同时观察到Ta2=0.20μs、Tb2=0.21μs。即同一点上的同时是绝对的。

这个例子能严格地证明相对性原理对于钟慢效应不成立（即钟慢效应不是双向的），有力地支持例1的结论。

【例3】有甲、乙两个惯性系，甲系中有一个静止的裸光源S，S在甲钟指示的t1和t2两个不同时刻分别发生一次闪光。从一个闪光点发出一次闪光，波阵面可围成一个球（简称波前球）。那两次闪光将产生两个波前球（球1和球2）。在甲系中观察，球1和球2是同心球。在乙系中观察，根据光速与光源的运动状态无关可得到球1和球2不同心的结论，而利用洛伦兹变换将甲系中的两个同心球——球1和球2变换到乙系中来却可得到与球1、球2对应的两个扁同心球—球1′和球2′。如果否认球1′和球2′是乙系中的观察者直接观察到的球1和球2，就必须否认洛伦兹变换是真实的时空变换；如果承认洛伦兹变换是真实的时空变换，则乙系中的观察者必须承认球1和球2既同心又不同心。矛盾无法消除。将甲系中的两次闪光事件改为放两次球状焰火事件，甲、乙两系中的观察者都承认那两个焰火球是同心的。由于光速与光源的运动状态无关，乙系中的人实际观测结果也是那样。这表明空间中的两个球不可能既同心又不同心。

【例4】在k′系中放置一架灵敏度足够高的双臂天平，臂与x′轴平行。在天平的两铁基吊盘下方各置一块电磁铁（两块电磁铁完全相同）。当电磁铁处于关闭状态而天平达到了平衡时，用两根脆弱细线斜拉住天平两臂和支柱。然后同时开启那两块电磁铁。k′系中的观察者必能观察到细线仍然完好无损。但在x轴与x′轴平行并沿x′轴运动的惯性系k中观察，由狭义相对论的相对同时推测，那两块电磁铁的开启不再是同时的，天平臂会受到非零转动力矩的作用而发生摆动，细线会被拉断。同一根细线不可能处于既断又不断的状态，因此，在k和k′两系中的观察者要么都能看到细线已断，要么都能看到细线未断（不可能一个看到已断而另一个看到是完好的）。如果k′系中的观察者看到细线完好无损，k系中的观察者必然也看到细线未断。这样，若同时的相对性是客观的，k系中的观察者就必须想信“对于一个运动的物体而言，一个非零转矩不能引起真实的旋转。“非零转动力矩能导致旋转”是一条经典物理定律（规律），相对论以维护物理学定律协变为目的却得到了必须破坏物理学定律协变的结果。

【例5】设一节固有长度为10米的火车在路基上以0.866c的速度行驶，路基前方有一个固有长度为8米的大坑。由尺缩效应和惯性系等价可知：在路基系中观察，火车收缩为5米可轻松地掉入8米长的坑内；在火车上观察，坑长收缩为4米，车头和车尾一样重的火车可越过此坑。相对论的支持者不能回答，火车是越过大坑还是嵌入坑内。

【例6】甲系中有一个静止的裸光源S，S发出一次闪光后形成一个波前球。在甲系中观察，该球的球心相对于甲系静止。但在乙系中观察，S是个运动的光源，由光速与光源的运动状态无关及不存在绝对静止系的前提可知，那个波前球的球心又必须静止在乙系之中。当甲、乙不是同一个惯性系时，同一个球心既相对于甲静止又相对于乙静止是不可能的。

【例7】K′系有一个绝原子光源，并沿x′轴发射了一个用来定义秒的光子。这个光子在K′系中有c′=λ′ν′的关系。现在站在k系中将c′、λ′、ν′分别变换到k系中来。由洛伦兹变换可知，变换过来的c=c′，变换过来的λ＞λ′,ν＞ν′，λν＞λ′ν′＞c′(或c)。也就是说变换过来的c、λ、ν之间不存在c=λν的关系。如果相对论效应是真实的，那么变换过来的c、λ、ν就是K系中一个对应的静止光源发出的光子的波速、波长和频率，它们之间应有c=λν的关系。如果相对论效应是影象效应，那么变换过来的c、λ、ν就在K系中找不到真实的对应也就不能保证真实的物理学定律协变（此例是不能保证c=λν协变）。

【例8】一列火车在路基上高速行驶。路基一侧有一道墙，墙上靠火车的一侧挂有小包炸药（炸药包与炸药包之间的距离超过殉爆距离）。火车靠墙一侧安有两个雷管（车头A′点一个，车尾B′点一个），雷管底部与路基系的墙上的小炸药包之间的距离短于殉爆距离。在火车上同时引爆A′和B′两处的雷管，那两个雷管又引爆了挂在路基系的墙上的A、B两处的小炸药包。由于同一点上的同时是绝对的，因此，火车系和路基系中的观察者都承认A、B两处的小包炸药的爆炸在火车系中是同时事件。又由于A、B两处的小炸药包爆炸事件是路基系中的事件，因此，路基系中的观察者可以根据“以相同速度传播的信号能否同时将A、B两处发生爆炸的信息传送到AB的中点M”来判断A、B两处的爆炸事件是否同时发生。可以利用的信号有光速信号、光纤中的亚光速信号、导线中的电脉冲信号、铯气室中的超光速信号、无风的空气中声音信号、钢轨中声音信号，甚至地上跑的玩具车（只要它们的速度控制精度足够高）。所利用的原理也不限于光速不变原理，而是更为广泛的速度对称原理。

参考文献：
1、 2 、维克多·韦斯科夫.二十世纪物理学家.杨福家等译。北京:科学出版社，1979
3、《世界上严肃的科学家冷眼看待相对论》 庄一龙
4、《 果壳中的宇宙》 史蒂芬. 霍金 著 吴忠超 译 湖南科学技术出版社 2002年2月
5、赵凯华，罗蔚茵. 新概念物理教程——力学. 北京：高等教育出版社，1995.
6 、上海科学技术出版社1964.8《狭义与广义相对论浅说》，31页

版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑

返回首页