Sunday, March 2, 2014

tw01 cai01 Leibniz微積分 差之和等於第一項與最後一項之差



作者：蔡聰明

episte.math.ntu.edu.tw/cgi/mathfield.pl?aut=%BD%B2%C1o%A9%FA‎
作者：蔡聰明，找到32 篇. 數學條目. 連續函數 · 蔡聰明 · 平均值定理 · 蔡聰明. 數學家小傳. Fermat, Pierre de · 蔡聰明. 文章（數學傳播）. 微積分與差和分大意 · 蔡聰明.
差之和等於第一項與最後一項之差




Leibniz 如何想出微積分


 
上頁　1│2│3│4│5│6　次頁
Leibniz 如何想出微積分？ （第 4 頁） 蔡聰明
 
．原載於數學傳播十八卷三期
．作者當時任教於台灣大學數學系
‧對外搜尋關鍵字


 
四、差和分學：從 Pascal 三角到 Leibniz 三角
在1672年春天，Leibniz 抵達巴黎，他的第一個成就是發現求和可以用求差來計算，即用減法可以求算加法。後來他曾描述他為何會想到差分以及差分的差分（即二階差分）等等的概念，並且強調差分扮演著他的所有數學思想的主角。在邏輯中，他徹底地分析真理，發現終究可化約成兩件事：定義與恆真語句 (indentical truths)。反過來，由恆真語句就可推導出豐碩的結果。他舉數列為例來展示：由 A=A 或 A-A=0 出發，可得

A-A + B-B + C-C + D-D + E-E = 0


即 A - (A-B) - (B-C) - (C-D) - (D-E) - E = 0 令 A-B=K, B-C=L, C-D=M, D-E=N, 則得

\begin{eqnarray*} & A-K-L-M-N-E=0 \\ & K+L+M+N=A-E \end{eqnarray*}


亦即差之和等於第一項與最後一項之差。 換言之，給一個數列 v=(vk)，考慮接續兩項之間的差

vk+1-vk=uk


所成的數列 u=(uk)，叫做（右）差分數列（還有左差分，同理可討論），那麼顯然有

\begin{eqnarray*} \sum^n_{k=1}u_k &=& (v_{n+1} - v_n) + (v_n - v_{n-1}) + \ldots + (v_2-v_1) \\ &=& v_{n+1}-v_1 \end{eqnarray*}


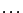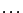採用登山的解釋就很明白了：想像山路鋪成台階，每一階相對於地面的高度為 v1, v2, $\ldots$, vn+1，而階差高度為 u1, u2, $\ldots$, un，那麼從甲地登到乙地共昇高

\begin{displaymath}u_1+u_2+\ldots+u_n=\sum^n_{k=1}u_k\end{displaymath}


另一方面這又等於 vn+1-v1，參見下圖 1。

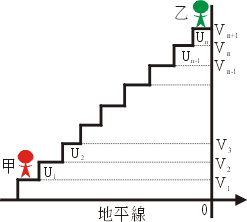
圖1

例子：考慮立方數列及其各階差分數列：

\begin{displaymath}\begin{array}{rrrrrrrr} 0 & 1 & 8 & 27 & 64 & 125 & 216 & \ld... ... 6 & 6 & \ldots \\ & & & & 0 & 0 & 0 & \ldots \\ \end{array}\end{displaymath}


由此我們立即讀出 1+7+19+37+61=125-0=125, 7+19+37+61+91=216-1=215, 6+12+18+24+30=91-1=90, 12+18+24+30=91-7=84。
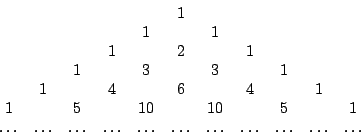
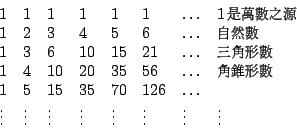
Leibniz 發現這個規律，覺得非常新奇、美妙，像小孩子玩積木一樣興奮不已。進一步，他研究 Pascal 三角（1654年，又叫算術三角）。Pascal 三角是作為開方、二項式展開、排列組合與機率之用，參見[2]，Leibniz 卻從中玩索出差和分的道理。下面我們列出 Pascal 三角常見的三種排法： (I)

\begin{displaymath}\begin{array}{ccccccccccc} & & & & & 1 & & & & & \\ & & & ... ...\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots\\ \end{array}\end{displaymath}


(II)

\begin{displaymath}\begin{array}{cccccc} 1 & & & & & \\ 1 & 1 & & & & \\ 1 & 2... ... 1 \\ \dots&\ldots&\ldots&\ldots&\ldots&\ldots \\ \end{array}\end{displaymath}


(III)

\begin{displaymath} \begin{array}{llllllll} 1 & 1 & 1 & 1 & 1 & 1 & \ldots & 1\m... ...vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ \end{array}\end{displaymath}


問題： 請說明上述 Pascal 三角的構成法。
在(II)的排列法中，斜對角線上的數相加，所得到的數恰好構成費氏數列(Fibonacci sequence)：
1, 1, 2, 3, 5, 8, 13, 21, …
這個數列含有許多美妙的性質，我們不預備講述。 由(III)的排列法中，Leibniz 立即讀出許多關於行或列求和的結果，例如

3+6+10+15 = (4-1) + (10-4) + (20-10) + (35-20) = 35-1 = 34


同理
10+20+35+56=126-5=121。
Leibniz 在巴黎遇到 Huygens 時，對 Huygens 描述他用求差來求和的結果，Huygens 立即建議他做下面富於挑戰性的問題。
問題：（Huygens 問題）
求無窮級數之和

\begin{displaymath}\sum^\infty_{k=1}{2\over k(k+1)}={1\over 1}+{1\over 3}+\cdots+{1\over {k(k+1)/2}}+\cdots \eqno(1)\end{displaymath}


這個問題涉及無窮多項的相加，它源自計算某種賭局 (a game of chance) 的機率。 這個級數每一項的分母恰是畢氏學派「形數」(figurate numbers) 中的三角形數：

因此，級數(1)就是三角形數的倒數之和。Leibniz 立即就求得這個和：因為

\begin{displaymath}{2\over k(k+1)}={2\over k}-{2\over k+1}\end{displaymath}


所以首 n 項之和為

\begin{displaymath}S_n=\sum^n_{k=1}{2\over k(k+1)}\\ =\sum^n_{k=1}({2\over k}-{2\over k+1})\\ =2-{2\over n+1} \end{displaymath}


從而

\begin{displaymath} \sum^\infty_{k=1}{2\over k(k+1)}=\lim_{n\to \infty}(2-{2\over n+1})=2 . \end{displaymath}


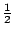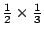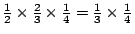我們在機率史的文獻上查不到 Huygens 的機率問題，不過我們倒有下面相關的例子：一個袋子裝有一個白球及一個黑球，從中任取一個球，若得白球就停止；若得黑球，則再填加一個黑球到袋中，變成兩黑一白，再任取一球，若得白球就停止；若又得黑球，則再添加一個黑球到袋中，變成三黑一白，如此繼續下去，那麼第一回合得白球的機率為 ${1\over 2}$，第二回合得白球的機率為 ${1\over 2}\times{1\over 3}$，第三回合得白球的機率為 ${1\over 2}\times{2\over 3}\times{1\over 4}={1\over 3}\times{1\over 4}$, … 等等，故終究得白球的機率為

\begin{displaymath} {1\over 2} + {1\over 2\times3} + {1\over 3\times 4} + \cdots + {1\over k(k+1)} + \cdots = 1 . \end{displaymath}


Leibniz 解決了 Huygens 問題後，進一步模仿 Pascal 三角，建構一個今日所謂的「調和三角」(harmonic triangle) 或 Leibniz 三角，一口氣解決了更多求無窮級數和的問題。 調和三角是這樣做成的：第一行排上調和數列，第二行依次排上第一行的前項減去後項之差，以後就按此要領做下去，結果如下：

\begin{displaymath}\begin{array}{rrrrrrrr} 1\over 1 & 1\over 2 & 1\over 3 & 1\ov... ...105 & \cdots &&&& \\ \vdots&\vdots&\vdots&&&&& \\ \end{array}\end{displaymath}


由此調和三角可以讀出

\begin{displaymath}{1\over 2}+{1\over 6}+{1\over 12}+{1\over 20}+{1\over 30}+\cdots=1\end{displaymath}


從而 Huygens 問題的答案是

\begin{displaymath}{2\over 2}+{2\over 6}+{2\over 12}+{2\over 20}+\cdots+{2\over k(k+1)}+\cdots=2\end{displaymath}


另外我們也可以讀出

\begin{displaymath}{1\over 3}+{1\over 12}+{1\over 30}+{1\over 60}+\cdots={1\over 2}\eqno(2)\end{displaymath}




\begin{displaymath}{1\over 4}+{1\over 20}+{1\over 60}+{1\over 140}+\cdots={1\over 3}\eqno(3)\end{displaymath}


等等。將(2)式乘以 3 就得到角錐形數的倒數之和：

\begin{displaymath}{1\over 1}+{1\over 4}+{1\over 10}+{1\over 20}+\cdots={3\over 2}\end{displaymath}


將(3)式乘以4就得到

\begin{displaymath}{1\over 1}+{1\over 5}+{1\over 15}+{1\over 35}+\cdots={4\over3}\end{displaymath}


同理也可得

\begin{displaymath}{1\over 1}+{1\over 6}+{1\over 21}+{1\over 56}+{1\over 126}+\cdots={5\over4}\end{displaymath}


Descartes 說得好：
由一個例子的考察，我們可以抽取出一條規律。
(From the consideration of an example we can form a rule.)
換言之，一個好的例子往往能夠反映出一般規律，即特殊孕育出普遍，或所謂的「一葉知秋」、「見微知著」的意思。我們由上述例子歸結出求和的共通模式 (pattern)：
定理 1：（差和分根本定理）
對於給定的一個數列 u=(un), n=1,2, …，如果可以找到另一個數列 v=(vn)，使得

un=vn+1-vn


那麼就有

\begin{displaymath}\sum^b_{n=a}u_n=v_{b+1}-v_a \eqno(4)\end{displaymath}


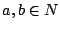其中 $a,b \in N$ 且 a<b。
我們引入適當的概念與記號：
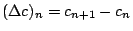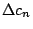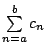定義： 設 c=(cn) 為一個數列，令數列 $\Delta c$ 為 $(\Delta c)_n=c_{n+1}-c_n$（簡記為 $\Delta c_n$）。 我們稱 $\Delta c$ 為數列 c 的（第一階）差分，Δ 為差分算子。 $\sum\limits^b_{n=a}c_n$ 叫做定和分（簡稱和分）。
因此，定理1 引出了兩個基本問題：
(i)研究差分算子 Δ 在運算上的基本性質。
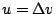(ii)已知一個數列 u=(un)，求另一個數列 v=(vn) 使得 $u=\Delta v$。
第一個問題很容易，在此從略。其次，利用(i)，第二個問題原則上也不難。在 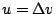$u=\Delta v$ 中，我們稱 v 為 u 的反差分數列或不定和分。事實上，已知數列 u=(uk), k=1,2, … 定義一個新數列 b=(bn) 如下：

\begin{displaymath}b_n=\sum^{n-1}_{k=1}u_k\eqno(5)\end{displaymath}


則易驗知 b=(bn) 滿足

\begin{displaymath}u=\Delta b\end{displaymath}


換言之，b=(bn) 就是 u=(un) 的一個不定和分。顯然，u 的不定和分不唯一，可以無窮多個（例如(5)式再加上任意常數都還是 u 的不定和分），但是任何兩個不定和分只差個常數。 對這一切作深入而有系統的研究就是差和分學的內容（包括差分方程）。差和分的學習對於微積分的了解非常有助益，因為兩者不過是離散與連續之間的類推與觀照而已。離散的差和分簡單明瞭，再連續化就得到了微積分。一般微積分教科書往往有如下的缺點：忽略差和分學，或類推與連續化處理得不好。
Posted by at

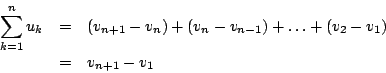
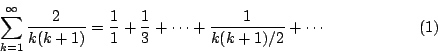
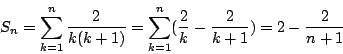
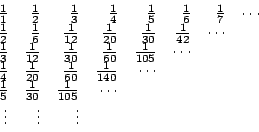
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)