http://boson4.phys.tku.edu.tw/high-school_math/geometry_1.html
得知空間彎曲需要曲率作為資訊,因此至少要有兩個維度,一個是切線方向,另一個是垂直於切線方向。另一考慮的角度,測度張量的定義 gij = ei · ej, 因此至少需兩個線性獨立的向量作基底才有最起碼的測度張量。這呼應我們前面講過的,一維生物不需要畢氏定理
幾何 (I)
形狀的數學、實驗的數學
想像力發揮、心中的小宇宙、"模型"光學與幾何
形狀、比例與相似性
從設計圖到完成品,形狀的相似性繪製地圖
Geo 希臘文原意是土地、測量。"幾何" 是徐光啟、利瑪竇翻譯。希臘的幾何成就
畢達哥拉斯定理:
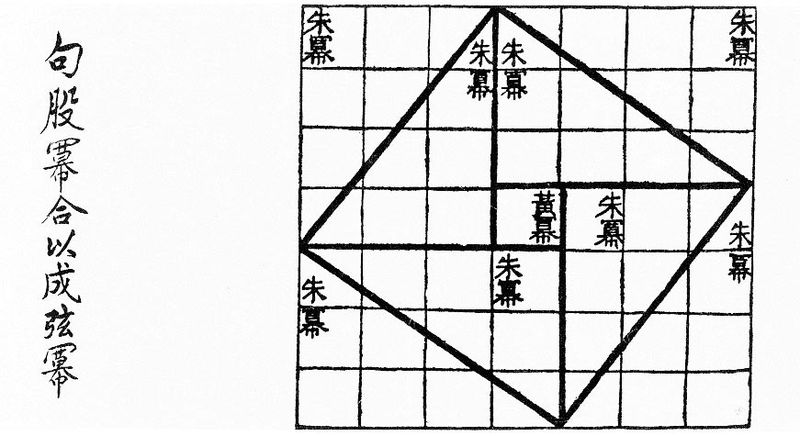
我們怎樣看畢氏定理?古中國叫"勾股弦定理"
古書中甚至轉述大禹因此治水成功,換用現代的語言,是應用數學原理成就精密的大型工程。
證明的方法很多,(但在此不採用三角函數的正餘弦定理 sin2θ + cos2θ = 1,這是因為這個三角函數的定理本身就是由畢氏定理證明出來的),以下介紹一個比之圖像化的證明。
(圖片出處:維基百科)
http://zh.wikipedia.org/zh-tw/勾股定理
多維度空間中長度的本質。即,長度與其投影在低維度裏的長度,它們之間有一定的關係。
誰不需要畢氏定理?
生存在一維空間中之智慧形式。歐基里德:公設與證明
古希臘數學家歐幾里得的《幾何原本》提出了五條公設。頭四條公設分別為:是直尺與圓規的幾何
第五條公設說:同一平面內一條直線和另外兩條直線相交,若在某一側的兩個內角的和小於兩直角,則這兩直線經無限延長後在這一側相交。
- 由任意一點到任意一點可作直線。
- 一條有限直線可以繼續延長。
- 以任意點為心及任意的距離可以畫圓。
- 凡直角都相等。
奧依勒的多面體公式
v - e + f = 2
其中 v、f、e 各代表 "頂點 (vertex)"、"面 (face)"、"邊 (edge)" 的數目。
http://140.128.93.186/~chents/MG11
如何理解
雕刻家的觀點
思考三角錐頂點、四角錐頂點、. . . n 角錐頂點,在截去一角 ( v' = v - 1 ) 來增加了一個面 ( f' = f + 1) 時的結果:同時也增加了 n 個邊 ( e' = e + n )
(值得注意的是,上述截角的動作是可 逆的。 )
可見 v' - e' + f' = v - e + f 會是常數
剩下的問題是,這個常數值是多少
考慮最簡單的四面體錐
1 + n = (n - 1) + ?
可見這個 "?" 是 2
一次截去兩個頂角可以嗎?這樣就不保證是凸形了。
(其他的證明方式可見維基百科或科普書)
證明 : http://plus.maths.org/content/eulers-polyhedron-formula
補充:高維度公式
( http://www.math.osu.edu/~fiedorowicz.1/math655/HyperEuler.html )
(幾何起源很早,與光學的關係也很密切)
為什麼近的東西看起來比較大?
視線從眼中射出?
反射與折射
面鏡與透鏡大一物理中的幾何光學
http://163.13.111.54/general_physics/week-08_day-1__geometrical_optics.html
解析幾何
座標
結合了函數與幾何,空間中的直線、曲線,都是函數或滿足某方程式的解。
向量空間(解析幾何與向量的關係)
向量:高中數學的定義?(數學)物件
維度?
線性獨立向量:大學物理學的定義
有 N 個向量,若任何一個都不能夠透過其他的向量線性組合而成,則這 N 個向講線性獨立。線性相依
無法構成線性獨立時稱之
座標轉換(詳見下次上課內容:幾何 II)向量空間:
該空間中有乘與加兩種操作。係數乘上基底向量是基本單元。向量是可以加減的,而係數(純量)則乘在向量上,要滿足一些規律,並構成封閉系統。向量間的內積與外積
(維基百科:http://en.wikipedia.org/wiki/Vector_space、MathWorld:http://mathworld.wolfram.com/VectorSpace.html)
(定義裏剛好也有談到 體(filed) 的,詳見 http://mathworld.wolfram.com/FieldAxioms.html)
向量的內積延伸知識:函數空間
我們為什麼想要知道向量的內積:(1) 想知道向量的長度 (2) 想知道向量的分量向量的外積
(幾何意義是:任一向量在另一向量上的投影大小,兩種作法的結果是一樣的。)(為什麼?)
我們為什麼想要知道向量的外積:電磁交互作用的勞倫玆力、描述轉動(但小心轉動本身不是向量、轉速才是,因此角動量仍是向量)。
(幾何意義是:兩向量撐開之面積大小、方向是撐開面之法方向。)(在三度空間就是體積嗎?不是,向量三重積,即 A · (B × C) 才是三個向量撐開來的平行六面體體積)
外積之大小等於張開之平行四邊形面積一事,是可以透過 :"移一塊補一塊" 的策略證明,請大家自行試試看。
更高維度的情形:n 個向量在 n 維空間張間來的體積,是該 n 個向量將各自分量排成矩陣後的行列式值。至於 n × n 矩陣的行列式值怎麼算,是有公式及規律性的。
作業:二維向量兩個求外積,試與其分量形式所組成的行列式值作比較。
(下次上課介紹)
三度空間裏的(數學)物件:點、線、面、體
直線
如何寫下一條直線的方程式?曲線
多問一句:如何寫下一個平面的方程式?
合宜的參數表示法
一條曲線是可以用參數來表示的,只要這個參數滿足一些基本的、不太離譜怪異的要求。
曲線的範例:
點集合 (x1, x2) 的一般形式用極座標表示
x1 = r cosθ , x2= r sinθ
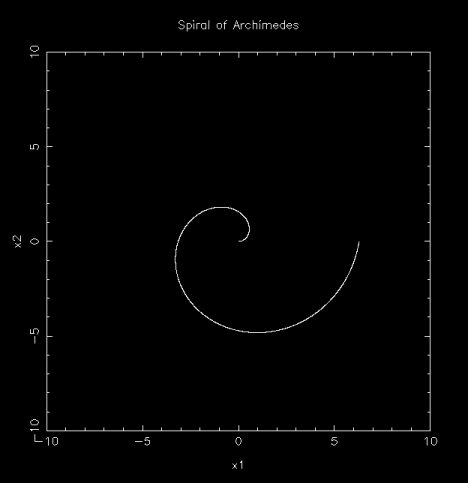
阿基米德螺線
依上面定義的 (x1, x2),其中
r = a θ , ( a ≠ 0 )
產生上圖的程式 spiral_of_archimedes.f
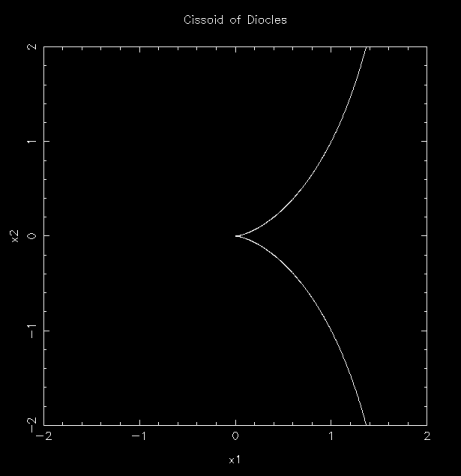
狄奧克勒斯 蔓葉線
r = 2 c sin2θ / cosθ , ( c ≠ 0 )
產生上圖的程式 cissoid_of_diocles.f
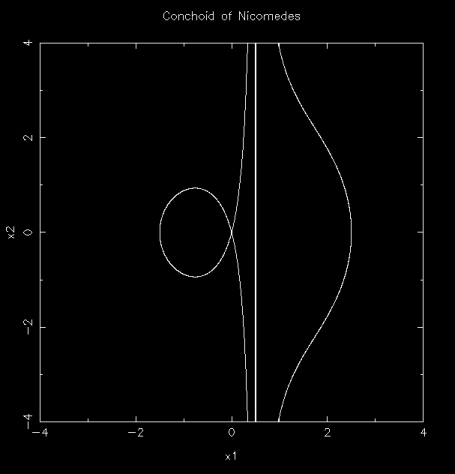
Conchoid (蚌線) of Nicomedes (不是 蚶線 limacon)
r = a / cosθ+ c , ( a ≠ 0, c ≠ 0 )
產生上圖的程式 conchoid_of_nicomedes.f
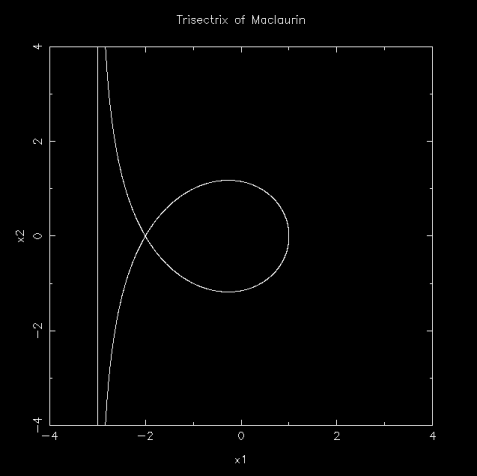
http://mathworld.wolfram.com/ConchoidofNicomedes.htmlTrisectrix (三等分角線) of Maclaurin
http://en.wikipedia.org/wiki/Conchoid_%28mathematics%29
r = a / cos(θ/3) , ( a ≠ 0, θ = 0 ~ 3π)
產生上圖的程式 trisectrix_f_maclaurin.f
曲線自身的參考座標
空間彎曲與否,是不是非得要跑到更高維度才看得出來?住在低維度空間的生物有什麼線索可用?(答案:非歐幾何時,歐氏幾何已建立的公設是不能用了。如三角形內角和大於 180 度)空間
事實上,即便二維都是很勉強的,因為那些生物都不可能有消化道(想像一下)。
有同學問,是否零維與一維就不知道或沒有所謂的空間彎曲?答案是的確如此:得知空間彎曲需要曲率作為資訊,因此至少要有兩個維度,一個是切線方向,另一個是垂直於切線方向。另一考慮的角度,測度張量的定義 gij = ei · ej, 因此至少需兩個線性獨立的向量作基底才有最起碼的測度張量。這呼應我們前面講過的,一維生物不需要畢氏定理。
平面
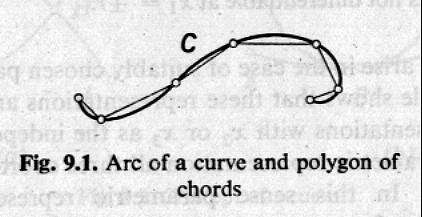
弧長作為曲線的自然參數
弧長的觀念,可以從多邊線段的長度來思考。上圖每一直線段都可由畢氏定理明確得出(因為我們知道那些點的 x 及 y 座標),故可加得總長。如果切分越來越細,而總長趨於某一定值極限。
這個 l 可以被證明將與選取參數表示法無關。(但這個 l 真的是我們所認知的弧長這種東西嗎?怎麼看出來?關鍵在 dx = (dx/dt) dt = x· dt,即 dx = √(dx · dx) = √(x· · x· ) dt )
弧長本身可以依其長度發展的變化而拿來當作一個表示曲線的參數,它與原參數之間的關係只要仿照上式定義來定成以下的形式即可:
利用這個定義,可證明(在此不列),弧長本身滿足作為曲線之參數表示法的規定要求,它的確是可以拿來作為描述曲線的參數。
以 dx = (dx1, dx2, dx3) 代表微小線段向量,則根據畢氏定理(二維的連套用兩次),可以確認 s 真的具有弧長的意義
範例:圓螺旋線
補充思考:
如果我們要用電腦去表現任何的曲線,不管拿到的是公式的 x(t) 或是數據的 X(I) ,我們都能自行建立合適的參數來繪圖。
這裏既然提出了弧長可做為參數使用了,則座標對參數之微分就有對特別的 s 及一般的 t 了,以下用 prime 及 dot 在符號上區分它們的不同:
斜率、曲率、扭率
切線方向(斜率)重要性質
曲線進展的方向是
上式有沒有除以 h 都沒有關係的。
取極限的情況,可得單位切(線)向量
如果換從在參數 t 的表象(表示法)裏,則有
利用以下性質(由 s(t) 的定義可看出)
便可得到
如此可以看得出它的確是單位向量 (小心切向量 t 與參數 t 是不同的東西)
曲率
切線方向如果一直不變,就是一條直線(相對於其所在的空間而言)。
如果切線單位向量隨著參數而改變,必定產生彎曲。將單位切線向量對弧長為分,得到以下的向量 k(s) (沒有特定命名,但依其方向定出的單位向量叫作法方向,後面會提到)
其大小叫作曲率 κ(s)
可定義 曲率半徑
不用弧長作參數,而以一般的參數表示曲率時,複雜很多(不重要,僅供參考)
切線變化方向的單位向量,又叫曲線的法向量 (Normal Vector) :
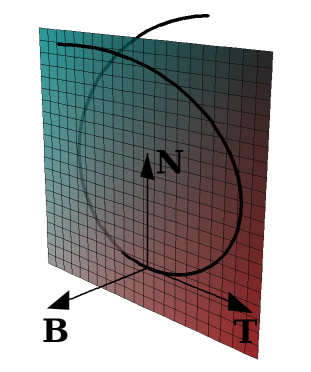
我們再定 bi-normal vector ,為突出垂直於 t 與 p 所張開的平面,下面談扭率的時候要用
t 、p 、 b 形成右手系座標軸
扭率
曲率測度曲線偏離切線方向直行的程度,而扭率則測度偏離密切面(osculating plane,即 t 與 p 構成的面)的程度(下圖中的 N 就是我們公式中定義的 normal vetor p)
我們可以看出
定為如下
由於 b' 與 p 平行,故扭率 τ 為
若將一條曲線的局部變化以泰勒展開式加以分祈,則會發現,以弧長為參數,以 t、p、b 為 x1、x2、x3 的座標軸,則 x1、x2、x3 的變化全由弧長、曲率與扭率決定,這個公式叫做正則表象(canonical representation)。
事實上,曲率與扭曲唯一決定了一條曲線(在不計位置的情況下)。(叫做 "空間曲線的基本定理",)
一個典型的例子,三角形內角和等於 180 度,(補充:三角形的外角和等於 360 度;凸多邊形的外角和是 360 度)曲面
http://dropwa.com/math/polygon/poly_3t.htm
裁縫師要能懂曲面的幾何,因為布是平面而衣服是立體的
曲面彎曲如何描述?(與曲線一樣,透過曲面法方向沿參數延伸時的變化)
曲面上能有直線嗎?(法向量是曲面的一個重要特徵量,曲面上的線在曲面法方向的投影,呈一直線者,即相當於曲面上的直線。)
曲面上之 "直線" 的特性:法向量投影後斜率沿發展方向不變,連接兩點間長度最短(測地線)。
如何在曲面上建立座標?
要用兩個參數 u1, u2 (在此用上標來標示參數,不是次方的意思),空間中的點則由 x(u1, u2) 來描述。
要作為一套合理的表面參數,須要求 x(u1, u2) 是 1-1 (1對1) 的對應。並且切線向量 t1 及 t2 有 t1 × t2 恆不為零
曲面的法向量
曲率
一個曲面有 first funcdamental form 及 second fundamental form 這兩個量。
高斯曲率
黎曼曲率張量
空間是幾何的舞台,抑或是演出者?
(問題:宇宙的空間膨脹,所有的東西都放大,對地球上生活的我們而言,不是都分不出來嗎?例如所謂膨脹的氣球圖像,在氣球上畫一隻螞蟻、則螞蟻不是會跟著膨脹嗎?)維度
我們自己是知道存在於(巨觀)的三度空間,這是因為此空間中兩點的距離是透過 s 2 = x2 + y2 + z2 而得來的
幾何學所認為的空問本質
空間可以彎,但局部仍是平的(只要取夠小的範圍看)
(反例:不可微分的函數)
前面的結論,弧長是曲線最自然的參數
也就是說,一維空間裏,兩點間的距離(長度)是最基本的。問如何定距離,只要推廣距離的定義,就推廣了空間的概念。
(想像我們定義一個量, 叫做 "離距" <- 在此亂創名詞一下, 見下:)
測度(metric,定距離,或 norm)
d(P,Q) 必須是實數、有限、非負值測度張量
d(P,Q) = 0 若且唯若 P = Q (即 P 與 Q 是同一個點)
d(P,Q) = d(Q,P)
d(P,Q) <= d(P,R) + d(R,Q) (其中 R 是異於 P, Q 的另一點,這一條件也叫做三角不等式)
(ds)2 = Σ gij dxi dxj
gij不再是 單位矩陣 I ≡ δij ,事情開始變得有趣。
例如,差距是 ( Δt, Δx, Δy, Δz ) 兩個時空點,其 (狹義相對頓論下之) 世界線的距離是:
Δs2 = -c2 (Δt)2 + (Δx)2 + (Δy)2 + (Δz)2
空間的平坦與彎曲
大家看過線的彎曲,能否想像面的彎曲及空間的彎曲?如何描述網格(網路)上的位置?是否存在像弧長那樣自然的表示法?
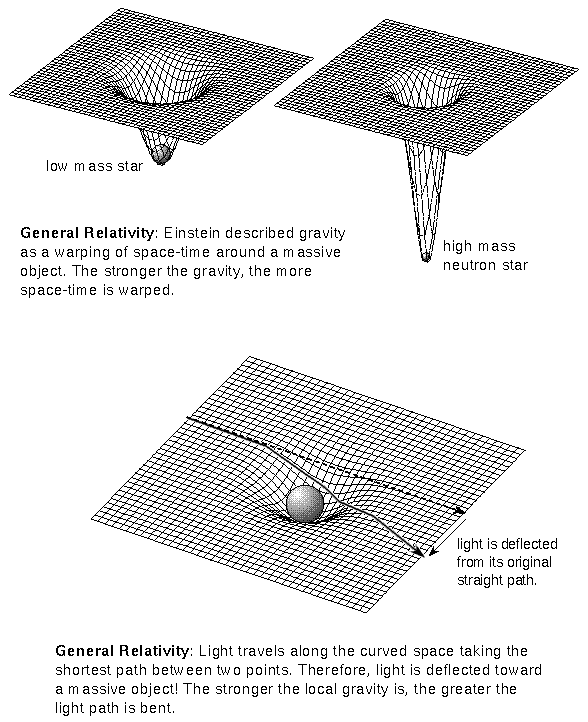
空間也是可以有曲率的,如同一個面(曲面)可以有曲率的那樣。
愛因斯坦方程式超簡介
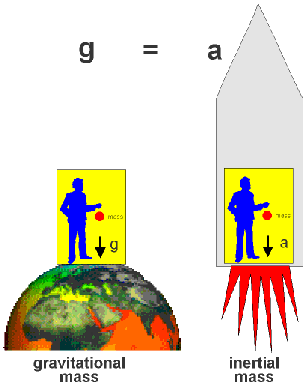
愛因斯坦在他的廣義相對論中提出,重力加速度與運動加速度是等效的(運動加速度會讓加速者看到光的彎曲,重力加也會),重力造成物體加速是因有質量的物質其週圍時空的曲率而造成。
水星進動與太陽背後的星光彎折(全日蝕才看得到)的預測,是此一理論的兩大勝利。
方程式的樣子如下:
G μν - Λ g μν = k T μν上式的意思是
時空曲率 - 宇宙項 = 物質密度其中 Λ是宇宙常數、k 是重力常數。裏頭為了營造出恆定宇宙(否則原方程式的解非膨脹即收縮),而設的扺消項。
1929 年在哈伯得到宇宙膨脹的證據時,愛因斯坦自稱這是他一生最大最錯誤。(有數據支持宇宙膨脹是加速之後,有人因此說,難到愛因斯坦的宇宙項終究還是加對了嗎?)
李明憲老師課程及教學網站

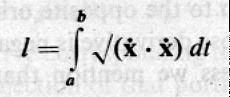
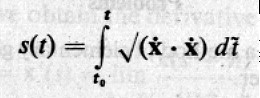
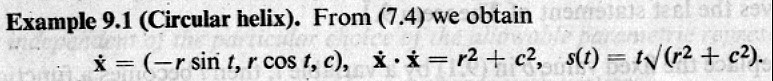
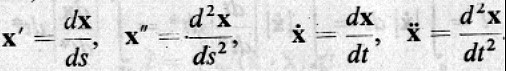
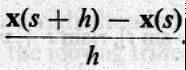
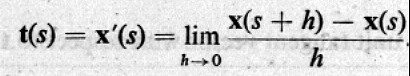
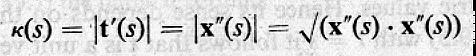
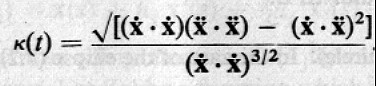
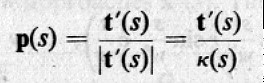
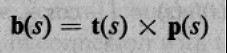
No comments:
Post a Comment