熱傳導方程式
维基百科,自由的百科全书
目录[隐藏] |
[编辑] 物理動機

一維熱方程圖解 (觀看動畫版)
- u =u(t, x, y, z) 表溫度,它是時間變數 t 與 空間變數 (x,y,z) 的函數。
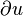 /
/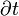 是空間中一點的溫度對時間的變化率。
是空間中一點的溫度對時間的變化率。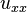 ,
, 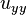 與
與 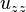 溫度對三個空間座標軸的二次導數。
溫度對三個空間座標軸的二次導數。- k 決定於材料的熱傳導率、密度與熱容。
如果考慮的介質不是整個空間,則為了得到方程的唯一解,必須指定 u 的邊界條件。如果介質是整個空間,為了得到唯一性,必須假定解的增長速度有個指數型的上界,此假定吻合實驗結果。
熱方程的解具有將初始溫度平滑化的特質,這代表熱從高溫處向低溫處傳播。一般而言,許多不同的初始狀態會趨向同一個穩態(熱平衡)。因此我們很難從現存的熱分佈反解初始狀態,即使對極短的時間間隔也一樣。
熱方程也是拋物線偏微分方程最簡單的例子。
利用拉普拉斯算子,熱方程可推廣為下述形式
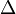 是對空間變數的拉普拉斯算子。
是對空間變數的拉普拉斯算子。熱方程支配熱傳導及其它擴散過程,諸如粒子擴散或神經細胞的動作電位。熱方程也可以作為某些金融現象的模型,諸如布莱克-斯科尔斯模型與 Ornstein-Uhlenbeck 過程。熱方程及其非線性的推廣型式也被應用於影像分析。量子力學中的薛丁格方程雖然有類似熱方程的數學式(但時間參數為純虛數),本質卻不是擴散問題,解的定性行為也完全不同。
就技術上來說,熱方程違背狹義相對論,因為它的解表達了一個擾動可以在瞬間傳播至空間各處。擾動在前方光錐外的影響通常可忽略不計,但是若要為熱傳導推出一個合理的速度,則須轉而考慮一個雙曲線型偏微分方程。
[编辑] 以傅立葉級數解熱方程
以下解法首先由約瑟夫·傅立葉在他於1822年出版的著作 Théorie analytique de la chaleur(中譯:解析熱學)給出。先考慮只有一個空間變數的熱方程,這可以當作棍子的熱傳導之模型。方程式如下:- x 是空間變數,所以 x ∈ [0,L],其中 L 表示棍子長度。
- t 是時間變數,所以 t ≥ 0。
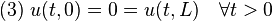 .
.
假設 λ < 0,則存在實數 B、C 使得
假設 λ = 0,則存在實數 B、C 使得
因此必然有 λ > 0,此時存在實數 A、B、C 使得
由此得到熱方程形如 (4) 的解。
一般而言,滿足 (1) 與 (3) 的解相加後仍是滿足 (1) 與 (3) 的解。事實上可以證明滿足 (1)、(2)、(3) 的解由下述公式給出:
[编辑] 推廣求解技巧
上面採用的方法可以推廣到許多不同方程。想法是:在適當的函數空間上,算子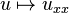 可以用它的特徵向量表示。這就自然地導向線性自伴算子的譜理論。
可以用它的特徵向量表示。這就自然地導向線性自伴算子的譜理論。考慮線性算子 Δ u = ux x,以下函數序列
[编辑] 非均勻不等向介質中的熱傳導
一般而言,熱傳導的研究奠基於以下幾個原理。首先注意到熱流是能量流的一種形式,因此可以談論單位時間內流進空間中一塊區域的熱量。- 單位時間內流入區域 V 的熱量由一個依賴於時間的量 qt(V) 給出。假設 q 有個密度 Q(t,x),於是
- 熱流是個依賴於時間的向量函數 H(x),其刻劃如下:單位時間內流經一個面積為 dS 而單位法向量為 n 的無窮小曲面元素的熱量是
- 熱傳導定律說明溫度對時間的梯度滿足以下線性關係
- 其中 A(x) 是個 3 × 3 實對稱正定矩陣。
- 溫度在 x 點對時間的改變率與流進 x 点所在的無窮小区域的熱量成正比,此比例常數與時間無關,而可能與空間有關,寫作 κ (x)。
- 在等方向性介質的情況,矩陣 A 只是個純量,等於材料的導熱率。
- 在非等向的情況, A不一定是純量,我們鮮少能明確寫出熱方程的解。然而通常可考慮相應的抽象柯西問題,證明它是適定的,並(或)導出若干定性結果(諸如初始值保持正性、無窮傳播速度、收斂至平衡態或一些平滑化性質)。這些論證通常有賴於單參數半群理論:舉例來說,如果 A 是個對稱矩陣,那麼由
[编辑] 粒子擴散
[编辑] 粒子擴散方程
在粒子擴散的模性中,我們考慮的方程涉及- 在大量粒子集體擴散的情況:粒子的體積濃度,記作 c。
- 在單一粒子的情況:單一粒子對位置的機率密度函數,記作 P。
如果擴散係數 D 依賴於濃度 c(或第二種情況下的機率密度 P),則我們得到非線性擴散方程。
單一粒子在粒子擴散方程下的隨機軌跡是個布朗運動。
如果一個粒子在時間
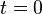 時置於
時置於 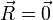 ,則相應的機率密度函數具有以下形式:
,則相應的機率密度函數具有以下形式: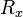 、
、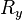 和
和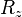 的關係是:
的關係是: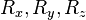 服從平均數為 0、變異數為
服從平均數為 0、變異數為 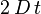 的正態分佈。在三維的情形,隨機向量
的正態分佈。在三維的情形,隨機向量 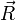 服從平均數為
服從平均數為 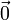 、變異數為
、變異數為  的正態分佈。
的正態分佈。在 t=0 時,上述
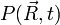 的表示式帶有奇點。對應於粒子處在原點之初始條件,其機率密度函數是在原點的狄拉克δ函數,記為
的表示式帶有奇點。對應於粒子處在原點之初始條件,其機率密度函數是在原點的狄拉克δ函數,記為 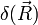 (三維的推廣是
(三維的推廣是 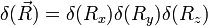 );擴散方程對此初始值的解也稱作格林函數。
);擴散方程對此初始值的解也稱作格林函數。[编辑] 擴散方程的歷史源流
粒子擴散方程首先由 Adolf Fick 於1855年導得。[编辑] 以格林函數解擴散方程
格林函數是擴散方程在粒子位置已知時的解(數學家稱之為擴散方程的基本解)。當粒子初始位置在原點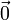 時,相應的格林函數記作
時,相應的格林函數記作 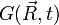 (t>0);根據擴散方程對平移的對稱性,對一般的已知初始位置
(t>0);根據擴散方程對平移的對稱性,對一般的已知初始位置 ,相應的格林函數是
,相應的格林函數是 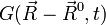 。
。對於一般的初始條件,擴散方程的解可以透過積分分解為一族格林函數的疊加。
舉例來說,設 t=0 時有一大群粒子,根據濃度分佈的初始值
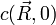 分佈於空間中。擴散方程的解將告訴我們濃度分佈如何隨時間演化。
分佈於空間中。擴散方程的解將告訴我們濃度分佈如何隨時間演化。跟任何(廣義)函數一樣,濃度分佈的初始值可以透過積分表為狄拉克δ函數的疊加:
[编辑] 一維格林函數解列表
以下以簡寫 BC 代表邊界條件,IC 代表初始條件。[编辑] 應用
熱方程在許多現象的數學模型中出現,而且常在金融數學中作為期權的模型出現。著名的布莱克-斯科尔斯模型中的差分方程可以轉成熱方程,並從此導出較簡單的解。許多簡單期權的延伸模型沒有解析解,因此必須以數值方法計算模型給出的定價。熱方程可以用 Crank-Nicolson 法有效地求數值解,此方法也可用於許多無解析解的模型(詳見文獻 Wilmott,1995)。熱方程在流形上的推廣是處理阿蒂亞-辛格指標定理的主要工具之一,由此也導向熱方程在黎曼幾何中的許多深入應用
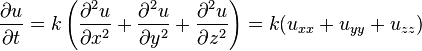


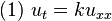
![(2) \ u(0,x) = f(x) \quad \forall x \in [0,L] \quad](http://upload.wikimedia.org/wikipedia/zh/math/c/a/5/ca5655ee90542959d5fa15ca07ff36e0.png)
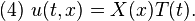
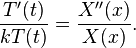
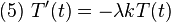
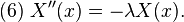

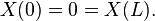
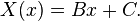
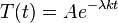
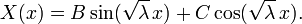
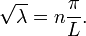
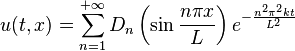
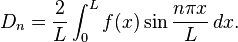
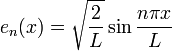
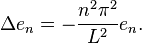
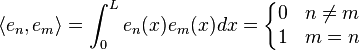

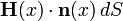
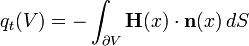
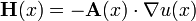
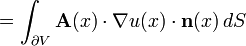
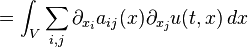
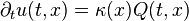
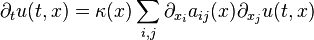
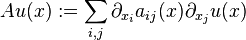
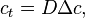
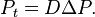
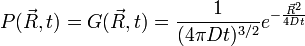

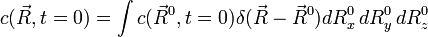
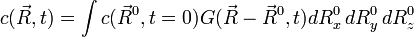
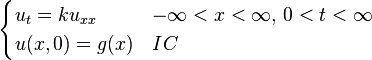
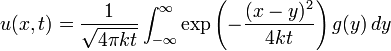
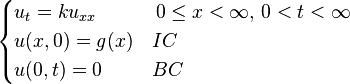
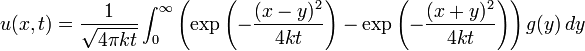
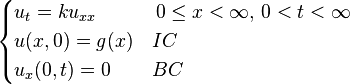
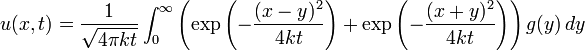
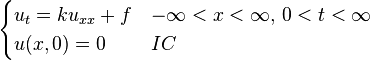
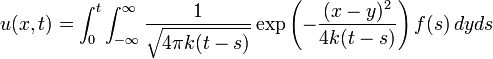
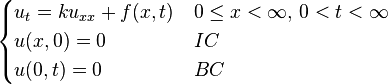
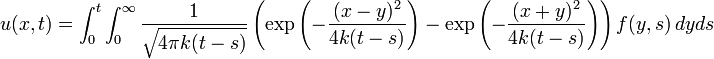


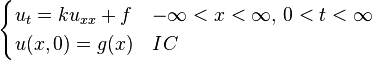
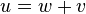
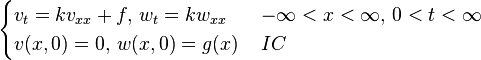
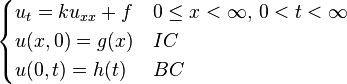

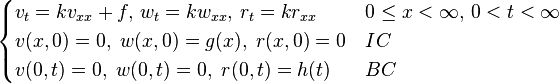
No comments:
Post a Comment