经典力学
维基百科,自由的百科全书
(重定向自牛顿力学)
目录[隐藏] |
[编辑] 簡介
经典力学是以牛顿运动定律为基础,以下分别列出三條牛顿运动定律:- 第一定律:倘物体处于静止状态,或呈等速直线运动,只要没外力作用,物体将保持静止状态,或呈等速直线运动之状态。这定律又称为惯性定律。
- 第二定律:物体的加速度,与所受的净外力成正比。加速度的方向与净外力的方向相同。即
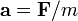 ;其中,
;其中, 是加速度,
是加速度,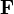 是净外力,
是净外力,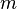 是质量。
是质量。 - 第三定律:两个物体的相互作用力总是大小相等,方向相反,同时出现或消失。强版第三定律还額外要求两支作用力的方向都處於同一直线。
由伽利略和牛顿等人发展出来的力学,着重于分析位移、速度、加速度、力等等矢量间的关系,又称为矢量力学。它是工程和日常生活中最常用的表述方式,但并不是唯一的表述方式:約瑟夫·拉格朗日、威廉·哈密頓、卡爾·雅可比等发展了经典力学的新的表述形式,即所谓分析力学。分析力学所建立的框架是近代物理的基础,如量子场论、广义相对论、量子引力等。
微分几何的发展为经典力学注入了蒸蒸日盛的生命力,是研究现代经典力学的主要数学工具。在日常经验范围中,采用经典力学可以计算出精确的结果。但是,在接近光速的高速度或強大重力場的系统中,经典力学已被相对论力学取代;在小距离尺度系统中又被量子力學取代;在同时具有上述两种特性的系统中则被相对论性量子场论取代。虽然如此,经典力学仍旧是非常有用的。因为下述原因:
雖然經典力學和其他“经典”理论(如经典电磁学和热力学)大致相容,在十九世纪末,还是发现出有些只有现代物理才能解释的不一致性。特别是,经典非相对论电动力学预言光波傳播於以太內的速度是常數,经典力学无法解释这预测,因而导致了狭义相对论的发展。经典力学和经典热力学的结合又导出吉布斯佯谬(熵不具有良好定義)和紫外灾难(在頻率趨向於無窮大時,黑體輻射的理論結果和實驗數據無法吻合)。为解决这些问题的努力造成了量子力學的發展。
[编辑] 理论的表述
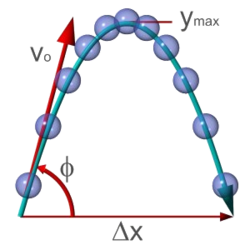
拋物線運動的理論分析屬於古典力學的領域。
以下介绍經典力學的几个基本概念。为简单起见,經典力學常使用点粒子来模拟实际物体。点粒子的尺寸大小可以被忽略。点粒子的运动可以用一些参数描述:位移、質量、和作用在其上的力。
实际而言,經典力學可以描述的物体总是具有非零的尺寸。(超小粒子的物理行为,例如電子,必须用量子力學才能正确描述)。非零尺寸的物体比虚构的点粒子有更复杂的行为,这是因为自由度的增加,例如棒球在移动的同时也可以旋转。虽然如此,点粒子的概念也可以用来研究这种物体,因为这种物体可以被视为由大量点粒子组成的复合物。如果复合物的尺寸极小于所研究问题的距离尺寸,则可以推断复合物的质心与点粒子的行为相似。因此,使用点粒子也适合于研究这类问题。
[编辑] 位置及其导数
| 国际单位制之導出單位 | |
| 位移 | m |
| 速度 | m s-1 |
| 加速度 | m s-2 |
| 轉动惯量 | kg m2 |
| 动量 | kg m s-1 |
| 角动量 | kg m2 s-1 |
| 力 | kg m s-2 |
| 力矩 | kg m2 s-2 |
| 能量 | kg m2 s-2 |
| 功率 | kg m2 s-3 |
| 压力 | kg m-1 s-2 |
| 表面張力 | kg s-2 |
| 輻照度 | kg s-3 |
| 动粘性 | kg m-1 s |
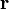 ;向量的端點為原点 O ,矢點為粒子所处地点。如果,点粒子在空间内移动,位置會随时间而改变,则
;向量的端點為原点 O ,矢點為粒子所处地点。如果,点粒子在空间内移动,位置會随时间而改变,则 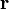 是时间
是时间 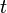 (从任意的初始时刻开始的时间)的函数。在爱因斯坦的相对性理论之前(伽利略相对性原理),时间被认为在所有参考系中是绝对的。也就是说,不同的观察者在各自的参考系中所测量的时间间隔都等值。并且,經典力學假设空间为欧几里得几何空间。
(从任意的初始时刻开始的时间)的函数。在爱因斯坦的相对性理论之前(伽利略相对性原理),时间被认为在所有参考系中是绝对的。也就是说,不同的观察者在各自的参考系中所测量的时间间隔都等值。并且,經典力學假设空间为欧几里得几何空间。位移是位置的改變。假設從舊位置
 改變到新位置
改變到新位置  ,則位移是
,則位移是 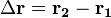 。使用向量分析的術語,假設一個粒子的位置,從舊位置移動到新位置,則位移是端點為舊位置,矢點為新位置的向量,又稱為位移向量。
。使用向量分析的術語,假設一個粒子的位置,從舊位置移動到新位置,則位移是端點為舊位置,矢點為新位置的向量,又稱為位移向量。[编辑] 速度
速度是位移对于时间的变化率,正式定义为位移对于时间的导数。以方程式表达 ;
;
 是速度。
是速度。在经典力学中,速度可以直接地相加或相减。例如,假设一辆车以向东 60 km/h 的速度超过另一辆以 50 km/h 向东的车,从较慢车的角度来看,它的速度是向东 60 − 50 = 10 km/h. 从较快车的角度来看,较慢车以 10 km/h 向西行驶。如果车是向北行驶呢?速度以向量形式直接相加;但必须用向量分析的方法来处理。
假设,第一辆车的速度为
 ,第二辆车的速度为
,第二辆车的速度为  ;其中,两辆车的速率分别为
;其中,两辆车的速率分别为 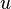 和
和 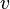 ,而
,而 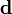 和
和  分别为两辆车朝着运动方向的单位向量。那麼,从第二辆车观察,第一辆车的速度
分别为两辆车朝着运动方向的单位向量。那麼,从第二辆车观察,第一辆车的速度 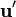 为
为 。
。
 为
为 。
。
 ,则这公式简化为
,则这公式简化为 。
。
 。
。
[编辑] 加速度
加速度,或是说速度对于时间的变化率,是速度对于时间的导数,以方程式表达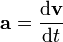 。
。
[编辑] 惯性参考系
思考同一事件在两个惯性参考系
 和
和  的测量结果。假设,相对于
的测量结果。假设,相对于  参考系,
参考系, 参考系以速度
参考系以速度  移动。分别处于这两个参考系的观查者会测量到以下结果:
移动。分别处于这两个参考系的观查者会测量到以下结果: (同一点粒子的运动,在
(同一点粒子的运动,在  测量的速度是在
测量的速度是在  测量的速度减去
测量的速度减去  )。
)。 (点粒子的加速度和惯性参考系无关)。
(点粒子的加速度和惯性参考系无关)。 (因为
(因为  )(施于点粒子上的力和惯性参考系无关; 参见牛顿运动定律)。
)(施于点粒子上的力和惯性参考系无关; 参见牛顿运动定律)。- 光速不是常数。
- 麦克斯韦方程组的形式不是独立于惯性参考系的;从一个惯性参考系转换到另一个惯性参考系,则麦克斯韦方程组的形式可能会改变。
[编辑] 力;牛顿第二定律
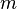 是点粒子的质量,而
是点粒子的质量,而 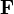 是所有作用在其上的力的向量总合(就是,净作用力),牛顿第二定律表明
是所有作用在其上的力的向量总合(就是,净作用力),牛顿第二定律表明 。
。
 为動量。
为動量。通常,質量
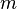 与时间无关。那麼,牛顿定律可以简化为
与时间无关。那麼,牛顿定律可以简化为 。
。
 是加速度。
是加速度。但质量并不总是独立于时间。例如,火箭需要喷出推进剂,才能往前方推进。所以,随着时间演化,火箭质量会渐渐减少。对于此案例,上述方程式并不正确,必须使用牛顿第二定律的完整形式。
牛顿第二定律不足以独立描述粒子的运动,还必需知道
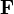 的性质和形式。假若,知道施加于点粒子的作用力,则牛顿第二定律足以描述粒子的运动。例如,一个典型的摩擦力
的性质和形式。假若,知道施加于点粒子的作用力,则牛顿第二定律足以描述粒子的运动。例如,一个典型的摩擦力  可以表达为:
可以表达为: 。
。
 是一个正值常数。
是一个正值常数。当每个施加於点粒子的作用力的独立关系都被设定後,它们可以被代入牛顿第二定律中,从而得到一个微分方程,称为运动方程。继续上面的例子,假設摩擦力是唯一作用在点粒子上的力,则运动方程为
 。
。
 ;
;
 是初始速度。此公式显示出,這粒子的速度是随着时间指数式递减到 0 。进一步将此公式积分,可以得到位移
是初始速度。此公式显示出,這粒子的速度是随着时间指数式递减到 0 。进一步将此公式积分,可以得到位移 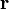 随着时间的函数。
随着时间的函数。重力和电磁学中的洛伦兹力是几种常见的力。
牛顿第三定律可以用来推论作用於粒子的力:如果已知粒子 A 作用於另一粒子 B 的力是
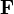 ,则粒子 B 会有一个大小相等、方向相反的反作用力
,则粒子 B 会有一个大小相等、方向相反的反作用力  作用於粒子 A 。
作用於粒子 A 。[编辑] 能量
若施加作用力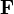 於某粒子,因而产生位移
於某粒子,因而产生位移 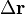 ,该作用力所做的功
,该作用力所做的功 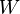 是一个标量
是一个标量 。
。
 是施加于粒子所有作用力所做的功,通过把每个作用力所做的功加起来得到,从牛顿第二定律:
是施加于粒子所有作用力所做的功,通过把每个作用力所做的功加起来得到,从牛顿第二定律: 。
。
 被称为動能。对于一个粒子,它被定义为
被称为動能。对于一个粒子,它被定义为 。
。
有一类特殊的力,称为保守力,可以表达为一个标量函数的梯度,该函数称为势能,标记为
 :
: 。
。
 是所有势能加起来得到的总势能,那麼,
是所有势能加起来得到的总势能,那麼, 。
。
 ,
,
 与时间无关。这结果非常有用。因为,很多常见的力是保守的。
与时间无关。这结果非常有用。因为,很多常见的力是保守的。[编辑] 進阶結果
牛頓的定律为复合物体提供了很多重要的结果。在这方面,牛頓定律延伸成为歐拉定律。描述一维运动的微积分也可以用来描述角動量的概念。经典力学有两种其它重要的表述:拉格朗日力学和哈密顿力学。它们都和牛顿力学相等价。但是,在解决问题上,它们经常有更大的威力。这些和其他的现代表述通常都绕过作用力的概念,而使用其他物理量,例如能量、拉格朗日量或哈密顿量,来描述力学系统。
[编辑] 經典变换
思考两个参考系 和
和  。对於分别处於这两个参考系的观察者,假设同一个事件在
。对於分别处於这两个参考系的观察者,假设同一个事件在  参考系中的时空坐标为(
参考系中的时空坐标为( ),在
),在  参考系中为(
参考系中为(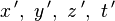 )。假若時間是有绝对性的(時間在两个参考坐标系的测量值相等),并且要求当
)。假若時間是有绝对性的(時間在两个参考坐标系的测量值相等),并且要求当 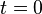 时,令
时,令  。假若
。假若  在
在  方向以
方向以 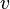 的速度相对于
的速度相对于  运动。那麼,同一事件在两个参考系
运动。那麼,同一事件在两个参考系  和
和  内的时空坐标关系为:
内的时空坐标关系为: 、
、 、
、 、
、 。
。
 超小於光速時,这变换是正确的。
超小於光速時,这变换是正确的。当解析某些问题时,采用旋转坐标(参考系)会带来很多便利。可以将旋转坐标与一个简易的惯性参考系保持映射函数关系,或者,也可提出虚假的离心力或科里奥利力。
[编辑] 歷史
古希腊的哲学家,包括亞里士多德在内,可能是最早提出“万有之本,必涵其因”论点,以及用抽象的哲理尝试敲解大自然奥秘的思想家。当然,对于现代读者而言,许多仍旧存留下来的思想是蛮有道理的,但并没有无懈可击的数学理论与對照實驗来阐明跟证实。而这些方法乃现代科学,如经典力学能形成的最基本因素。约翰内斯·开普勒按照因果關係来解释行星运动的科学家。他从第谷·布拉赫对火星的天文观测资料裏发现了火星公转的轨道是椭圆形的。这与中世纪思维的切割,大约发生在西元1600年。差不多于同时,伽利略用抽象数学定律来解释粒子运动。传说他曾经做过一个很有意思的實驗:他从比萨斜塔扔下两个不同质量的球,试验这两个球是否会同时落地。虽然这传说很可能只是传说。但他确实做过在斜面上滚球的属量性实验;他的加速运动论显然是由这类实验的结果推导出的,而且成为了经典力学的基础。
牛顿在他的巨著《自然哲学的数学原理》裡发表了三条牛顿运动定律;慣性定律,加速度定律和作用与反作用定律。应用这些定律,他能够计算出普通物体与天体的运动轨道。特别值得一提的是,他研究出开普勒定律在理论方面的详解。牛頓先前创发的微积分是研究经典力学所必备的数学工具。
牛頓和那时期的同仁,除了克里斯蒂安·惠更斯为值得注意的例外,大多数都认为经典力学应可以诠释所有大自然的现象,包括用其分支學術,几何光学,来解释光波。甚至于他发现的牛頓環(一个光波干涉现象),牛頓都試著用自己的光微粒学说来解释。
十九世纪后期,尖端的理论与实验发掘出许多扑硕迷离的难题。经典力学与热力学的连结导至出经典统计力学的吉布斯佯谬(熵不是个良好定义的物理量)。在原子物理的领域,最基本的问题,像原子模型和發射光譜,经典力学都无法给出合理的解释。眾位大师尽心竭力研究这些难题,成功地发展出现代量子力学。类似地,在座标转换时(转换于两个移动参考系之间),因为经典电磁学和经典力学相互矛盾,表现出不同的物理行为,引起爱因斯坦的关注,经过多年的努力,终就想出惊世的相对论。
自二十世纪末期以後,不再能虎山独行的经典力学,与经典电磁学共同被牢牢的嵌入相对论和量子力学裏面,成为在非相对论性和非量子力学性的極限,研究非相对论性和非量子尺寸物体的物理性质的学术。
[编辑] 适用域
大多数经典力学的理论是更精准理论的简化或近似。两个非常精准的學術领域是广义相对论和相对论性统计力学。几何光学是量子光学的近似,并没有比它更优良的经典理论了。[编辑] 狭义相对论的近似
在牛顿力学,或非相对论性经典力学裏,一个粒子的动量 表达为
表达为 ;
;
 是粒子的质量,
是粒子的质量, 是粒子的速度。
是粒子的速度。在相对论裏,动量表达为
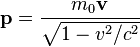 。
。
 是粒子的静止质量。
是粒子的静止质量。这表达式可以对项目
 泰勒展开为
泰勒展开为 。
。
 ,速度超小于光速时,经典近似成立。
,速度超小于光速时,经典近似成立。举例而言,回旋加速器,磁旋管,或高电压磁控管的相对论性回旋頻率
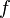 为
为 ;
;
 是电子的经典頻率 ,
是电子的经典頻率 ,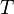 是动能 。
是动能 。电子的靜止質量是 511KeV。假若,电磁真空管的直流加速电压为 5.11KeV ,那麼,頻率修正很小,只有 1% 。
[编辑] 量子力学的近似
当系统尺寸接近德布罗意波长时,经典力学的射线近似不成立,粒子具有波动性质。根据德布罗意假说,非相对论性粒子的波长是 ;
;
 是普朗克常数。
是普朗克常数。因为电子的质量较轻,不需要擁有很大的動量,就會顯示出波動現象。克林顿·戴维孙和雷斯特·革末首先觀察到电子的波动性质。於 1927 年,他们在戴維森-革末實驗中,将以 54V 加速,电子波长为 0.167 nm 的電子束,入射於原子间隔为 0.215 nm 的鎳晶體標靶.。細心地測量散射到每個角度的電子束強度,就可以得到電子的繞射圖案,與威廉·布拉格預測的 X射線繞射圖案完全相同。
在电子工程领域,有显示经典力学不足的更实际例子,像穿隧二極體和积体电路內電晶體閘極的量子穿隧效應。

No comments:
Post a Comment