 定义为在单位时间内,垂直於传播方向上的单位面积内能量对时间的平均值,即玻印亭矢量对时间的平均值
定义为在单位时间内,垂直於传播方向上的单位面积内能量对时间的平均值,即玻印亭矢量对时间的平均值
 这个量来表征。对於单色光波场,电矢量
这个量来表征。对於单色光波场,电矢量 可以写为
可以写为 是复振幅矢量,在笛卡尔直角坐标系下可以写成分量的形式
是复振幅矢量,在笛卡尔直角坐标系下可以写成分量的形式 。
。这里
 是在三个分量上的(实)振幅,对於平面波
是在三个分量上的(实)振幅,对於平面波 ,即振幅在各个方向上是常数。
,即振幅在各个方向上是常数。 是在三个分量上的相位,
是在三个分量上的相位, ,
, 是表征偏振的常数。
是表征偏振的常数。要计算这个平面波的光强,则先计算电场强度的平方:
 、
、 ,如果它们在空间中某点发生重叠,则根据叠加原理,该点的电场强度是两者的矢量和:
,如果它们在空间中某点发生重叠,则根据叠加原理,该点的电场强度是两者的矢量和: 。
。
 、
、 是两列波各自独立的光强,而
是两列波各自独立的光强,而 是干涉项。 我们用
是干涉项。 我们用 、
、 表示两列波的复振幅,则干涉项中
表示两列波的复振幅,则干涉项中 可以写为
可以写为 、
、 可以在笛卡尔坐标系下分解为
可以在笛卡尔坐标系下分解为
倘若在各个方向上,两者的相位差
 都相同并且是定值,即
都相同并且是定值,即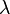 是单色光的波长,
是单色光的波长, 是两列波到达空间中同一点的光程差。
是两列波到达空间中同一点的光程差。此时干涉项对光强的贡献为
 时有极大值
时有极大值 ;当
;当 时有极小值
时有极小值 。
。特别地,当两列波光强相同即
 时,上面公式可化简为
时,上面公式可化简为 ,此时对应的极大值为
,此时对应的极大值为 ,极小值为0。
,极小值为0。
 作为条纹清晰度的量度:
作为条纹清晰度的量度: ,即可见度的范围为0到1之间。
,即可见度的范围为0到1之间。
![\mathbf{E}(\mathbf{r}, t) = \frac{1}{2}\left [\mathbf{A}(\mathbf{r})e^{-i \omega t} + \mathbf{A}^{*}(\mathbf{r})e^{i \omega t}\right ]\,](http://upload.wikimedia.org/math/e/d/e/ede56cccf56cca05147817f71b2add2d.png)
![\mathbf{E}^2 = \frac{1}{4}\left [\mathbf{A}^2e^{-2i \omega t} + \mathbf{A}^{*2}e^{2i \omega t} + 2\mathbf{A} \cdot \mathbf{A}^{*}\right ]\,](http://upload.wikimedia.org/math/3/f/6/3f67a46d9d74a796766024050317f092.png)


![\begin{align}
\mathbf{E}_1 \cdot \mathbf{E}_2 & = \frac{1}{4} \left [ \mathbf{A}e^{-i\omega t} + \mathbf{A}^{*}e^{i\omega t} \right] \left [ \mathbf{B}e^{-i\omega t} + \mathbf{B}^{*}e^{i\omega t} \right]\\
& = \frac{1}{4} \left ( \mathbf{A}\cdot \mathbf{B}e^{-2i\omega t} + \mathbf{A}^{*}\cdot \mathbf{B}^{*}e^{2i\omega t} + \mathbf{A}\cdot \mathbf{B}^{*} + \mathbf{A}^{*}\cdot \mathbf{B} \right )
\end{align}
\,](http://upload.wikimedia.org/math/8/f/f/8ffeeeacff4f4d117df6a14aff52a1ed.png)







No comments:
Post a Comment