维基百科,自由的百科全书
 。
。
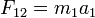 。
。
 。
。
 。
。
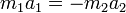 。
。
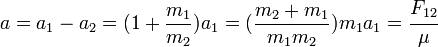 。
。
- 約化質量通常用希臘字母
 來標記。
來標記。 - 這兩個物體中,任何一個物體的質量,都小於約化質量。
- 假若物體 1 的質量超大於物體 2 的質量,
 ,則可以取物體 2 的質量為約化質量的近似值:
,則可以取物體 2 的質量為約化質量的近似值: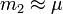 ;也可以視物體 1 為固定的,只有物體 2 在移動。
;也可以視物體 1 為固定的,只有物體 2 在移動。
自由落體和圓周運動
自由落體與圓周運動
有沒有道理?
自由落體和圓周運動有什麼共通性?
年輕的牛頓一直在想:蘋果會掉下來,但月球為什麼不會掉下來?(這真是一個好問題啊!)
伽利略的慣性定律:『不受外力作用的物體,沿一直線作等速度運動』。
牛頓把它運用在地球與月球的系統上;如果地球對月球沒有任何作用力的話,月球將沿著圓形軌道的切線方向飛出去,然而月球並沒有飛出去,依然在圓周上繞著地球運轉,這表示月球一定受到地球的引力而被拉住。換句話說:月球一直沿著圓形軌道的切線方向飛出,但地球的引力一直把月球拉著掉下來,結果,月球永遠在圓形軌道上運動。
蘋果從樹上掉下來(自由落體)和月亮繞地球轉(圓周運動)受到的都是同一種力,這個力就是『萬有引力』。
那麼這個引力有多大呢?在定性的問題解決之後,牛頓接著想到定量的問題。
延伸學習:
除了都是受到『萬有引力』之外,蘋果和月亮都感受有一種同樣的感覺,那就是『失重』。
萬有引力定律
地球對於蘋果和月球都有相同性質的吸引力,
根據月球的圓形軌道半徑與其公轉週期,可以得知月球受到地球的引力,是月球在地球旁邊時所受引力的1/3600倍,月球的軌道半徑大約等於地球半徑的60倍,牛頓想:這是否代表引力的大小與離開地球距離的平方成反比?於是,萬有引力定律產生了:『宇宙間的一切物體,彼此有一個吸引力的作用,其大小與質量的乘積成正比,與兩物體間的距離平方成反比。』。
那麼,行星與太陽之間有沒有這一種力呢?根據刻卜勒的行星運動第一定律:行星的軌道是一個橢圓,太陽在兩個焦點之一。牛頓把行星的軌道假設為圓形,予以簡化;行星繞著太陽的運動,就像月球繞著地球運動一樣的情形了。
再與刻卜勒第三定律驗證一下?該定律說:行星軌道距離的三次方與行星週期的平方的比值是固定的。牛頓利用行星的軌道距離與週期的關係,來計算太陽與行星之間的作用力,居然與他的萬有引力定律相吻合。這樣,牛頓確信這個定律能夠適用於宇宙間的一切物體。
 牛頓蘋果的故事
牛頓蘋果的故事
【參考資料】
相關網頁:
自由落體、牛頓、牛頓蘋果的故事
BACK to 牛頓
BACK to 物語悟理
最近更新時間: Fri, 10/08/2004 7:37 PM
 邱韻如
邱韻如
最近更新時間: Fri, 10/08/2004 7:37 PM
自由落體與圓周運動
- 蘋果與月亮到底有什麼關係?
- 自由落體與圓周運動的共通性
- 萬有引力(Gravitation)
- 失重
- 什麼時候會『失重』?
- 真的失去重量了嗎?
- 坐電梯與坐太空船
- 玩自由落體
- 真的失去重量了嗎?
- 什麼時候會『失重』?
有沒有道理?
自由落體和圓周運動有什麼共通性?
年輕的牛頓一直在想:蘋果會掉下來,但月球為什麼不會掉下來?(這真是一個好問題啊!)
伽利略的慣性定律:『不受外力作用的物體,沿一直線作等速度運動』。
牛頓把它運用在地球與月球的系統上;如果地球對月球沒有任何作用力的話,月球將沿著圓形軌道的切線方向飛出去,然而月球並沒有飛出去,依然在圓周上繞著地球運轉,這表示月球一定受到地球的引力而被拉住。換句話說:月球一直沿著圓形軌道的切線方向飛出,但地球的引力一直把月球拉著掉下來,結果,月球永遠在圓形軌道上運動。
蘋果從樹上掉下來(自由落體)和月亮繞地球轉(圓周運動)受到的都是同一種力,這個力就是『萬有引力』。
那麼這個引力有多大呢?在定性的問題解決之後,牛頓接著想到定量的問題。
延伸學習:
除了都是受到『萬有引力』之外,蘋果和月亮都感受有一種同樣的感覺,那就是『失重』。
萬有引力定律
地球對於蘋果和月球都有相同性質的吸引力,
根據月球的圓形軌道半徑與其公轉週期,可以得知月球受到地球的引力,是月球在地球旁邊時所受引力的1/3600倍,月球的軌道半徑大約等於地球半徑的60倍,牛頓想:這是否代表引力的大小與離開地球距離的平方成反比?於是,萬有引力定律產生了:『宇宙間的一切物體,彼此有一個吸引力的作用,其大小與質量的乘積成正比,與兩物體間的距離平方成反比。』。
那麼,行星與太陽之間有沒有這一種力呢?根據刻卜勒的行星運動第一定律:行星的軌道是一個橢圓,太陽在兩個焦點之一。牛頓把行星的軌道假設為圓形,予以簡化;行星繞著太陽的運動,就像月球繞著地球運動一樣的情形了。
再與刻卜勒第三定律驗證一下?該定律說:行星軌道距離的三次方與行星週期的平方的比值是固定的。牛頓利用行星的軌道距離與週期的關係,來計算太陽與行星之間的作用力,居然與他的萬有引力定律相吻合。這樣,牛頓確信這個定律能夠適用於宇宙間的一切物體。
【參考資料】
- 懷特著,陳可崗譯:牛頓(上)-最後的巫師,天下文化,ISBN 957-621-969-8。
- 懷特著,陳可崗譯:牛頓(下)-科學第一人,天下文化,ISBN 957-621-970-1。
- 郭奕玲、沈慧君著:物理通史,凡異出版社,ISBN
957-694-157-1。
- 郭奕玲、沈慧君著:物理學演義,凡異出版社,ISBN 957-694-245-4。
- 繆克成:論作用中的反作用-力學的故事,凡異出版社,ISBN 957-694-286-1。
相關網頁:
自由落體、牛頓、牛頓蘋果的故事
BACK to 牛頓
BACK to 物語悟理
最近更新時間: Fri, 10/08/2004 7:37 PM
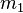 與
與 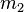 ,環繞著兩個物體的
,環繞著兩個物體的
No comments:
Post a Comment