狄拉克δ函数Dirac delta function股票数学模型对冲基金方法
标签:
股票数学模型对冲基金股票 |
分类: 股票数学模型 |

狄拉克δ函数的顺序零为中心的正态分布的限制(在这个意义上的分布)
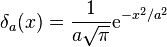 作为
作为 
线箭头之上,狄拉克δ函数的示意图。
概述
的δ函数的曲线图通常被认为是以下整个x轴方向和y轴正。
狄拉克δ是用来模拟一个高大的窄脉冲函数(
[
这等于是引入δ-函数的形式:
合理使用的理论分布
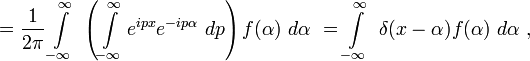
其中的δ-函数被表示为:
- “经典的傅立叶变换的最大的缺点是一个相当狭窄的类功能(原稿),它可以有效地计算,即,它是必要的,这些功能足够迅速下降至零(附近为无穷大),以便确保傅里叶积分的存在,例如,这样的简单的功能作为多项式的傅立叶变换,在传统意义上不存在。经典的傅立叶变换进行分布的扩展大大扩大的类可转化的功能,而这除去许多的障碍。“
进一步的发展,包括泛化的傅立叶积分,“开始Plancherel的开创性大号
无穷小公式为无限高,单位冲激δ函数的柯西分布
[
狄拉克δ可以松散地想作为一个功能上的实线,这是零无处不在原点,它是无限的除外,
也约束满足身份
[
严格地定义δ函数的方法之一是作为一个措施
[
不被认为是一个广义函数的理论分布的函数本身,但只有在它是如何影响其他功能时,对他们的“整合”。
每一个测试函数φ。
对于δ是正确的分布,它必须是在适当的意义上的“连续”。
直观地说,如果集成的部件被允许,那么后者的积分简化为
而事实上,部分积分法的一种形式是允许为Stieltjes积分,并在这种情况下,一个确实有
Dirac测度测度论的背景下,产生了一个整合分布。
[
是的delta量或单位质量集中在
在一个局部紧Hausdorff空间 

[
[
delta函数满足下面的缩放属性为一个非零的标量α:
等
特别是,delta函数是一个偶数的分布,在这个意义上
这是均匀度-1。
[
相反,如果所述ƒ(x)的=
[
的积分的时间延迟的狄拉克δ由下式给出:
它如下与时间延迟的狄拉克δ的函数f(t)的卷积的效果相同的量是f(t)的时间延迟:
-

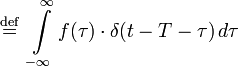
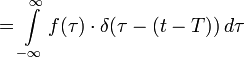
(使用( 4 ): 
) 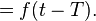
[
更一般地,三角形分布可以由具有光滑的函数g(x),在这样一种方式,熟悉的变化的变量式持有,那
G 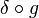
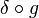
因此,这是很自然的定义的组合物的δ(G(X))为连续可微函数
其中求和延伸过所有的g(x)的根,它被假定为简单。
在积分形式的广义标度特性可写为
[
三角洲分布在n维空间中满足下列公式的属性,而不是:
紧支撑函数ƒ。
使用coarea从几何测量理论
[
所有施瓦茨函数φ。 

也就是说,δ是一个身份的元素的卷积脾气分布的,其实紧支撑的空间分布的卷积是一个关联代数与身份的增量功能。
傅立叶逆变换的回火分布ƒ(ξ)= 1的δ函数。
更严格的,它遵循自
施瓦茨功能ƒ。
在这些方面,delta功能提供了一个R
当然,这是速记的断言的傅立叶变换的回火分布
是
这再次通过施加自伴性傅里叶变换如下。
[
狄拉克δ分布的分布衍生的是的分布δ'紧支平滑的函数φ定义[38]。
这里的第一个平等是一种整合的部分,如果δ是一个真正的函数,然后
的第k个衍生物的δ的定义类似分布上给出测试功能
特别是δ是一个无限可微的分布。
的δ函数的一阶导数的分配限制的差商:
更适当地,一个具有
其中τh是平移算符,由τHφ(x)的=φ(+ h)的功能上定义,并且在分布
的衍生物的delta函数满足一些基本性质,包括:
此外,卷积是一个紧支撑的光滑函数fδ'
如下从属性的分配衍生物的卷积。
[
即,α
delta函数的第一部分的衍生物被认为是沿着坐标平面的双层
[
delta函数序列的功能的限制,可以被看作是
其中ηε(X)有时也被称为一个新兴的增量功能
所有连续函数ƒ具有紧凑的支持
[
通常一个新生delta函数ηε可以以下面的方式构造。
在n维空间中,而使用缩放
以这种方式构造的ηε是已知的作为一个近似的身份
这是所有的连续和紧凑的支持,虽然并不顺利,因此不是一个磨光。
[
在概率论的上下文中,这是很自然的,施加的附加
条件是初始η1在一个近似的身份应该是正面的,然后,这样的函数表示的概率分布
另一个例子是的Wigner半圆分布
这是连续的,紧支撑,但不是一个磨光的,因为它是不光滑。
[
对于所有的ε,δ>
0。
在实践中,接近δ函数的半群的出现,
在这种限制是通常理解意识的淡薄。
物理上重要的卷积半群所产生的这样的根本的解决方案的一些例子包括以下内容。
- 热内核
所定义的热内核
以概率论
在高维欧氏空间R
- Poisson核
运营商的严格定义为Fourier乘
[
在波的传播和波动力学等物理领域,涉及的双曲方程,因此可能有更奇异的解决方案。
虽然使用傅立叶变换,可以很容易地看到,这会产生一个半群在某种意义上,它是绝对可积的,所以不能定义一个半群在上述强烈的责任感。
一个无限大的弹性绳平衡的解决方案,u表示位移,与初始扰动的起源。
其他的身份,这种近似的正弦函数
[
一个线性偏微分方程的研究方法之一
当
其中
一些向量ξ。
作为一种弱的衍生物,这样,这个方程被表示为任何测试函数φ,这里被解释的拉普拉斯
结果如下从牛顿潜在的公式(从根本上解决泊松方程)。
其中Rφ(ξ,p)的Radon变换的φ:
另一种等价表达式的平面波分解,,从Gel'fand
Shilov(1966年至1968年
N
N
[
另请参阅:
傅立叶级数的研究中,一个重要的问题,包括确定是否以及在何种意义上的傅立叶级数与一个周期函数收敛的功能。
因此,
哪里
初等傅立叶系列状态的一个基本结果的Dirichlet内核的倾向的倍数的δ函数为
每一个紧支撑的光滑函数f。
在区间[-π,π]。
每一个紧支撑的连续函数f。
[
狄拉克δ分布是一个密集的定义
- Sobolev空间
自动连续的,且满足特别
[
更一般地,让H
[
系数{αn}的发现:
这也可以由符号表示:
让我代表的的身份运营商的希尔伯特空间,表达
是积分算子,和ƒ的表达式可以重写为:
右手侧收敛到ƒ
导致δ函数表示:
与合适的操纵希尔伯特空间
[
柯西用一个无限小的α写下一个单位的冲动,无限又高又窄的的狄拉克类型δ函数δα满足 

现代集合论方法允许我们定义无穷小,通过的的神州泰岳建设,一个空序列将变成一个无限小的在这个意义上的等价类的关系定义在一个合适的超滤模。 

[
主要文章:

狄拉克的梳子是狄拉克δ函数的无穷级数的间隔周期
这是一个在每个整数点群众序列。
特别地,
[
Sokhatsky的公式[59]
据了解,在这里的极限分布感,紧支撑光滑函数ƒ,
[
同样,对于任何真正的或复杂的价值R
这表现为克罗内克δ函数的Diracδ函数作为一个独立的模拟[60]
。
[
在概率论和统计 
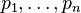
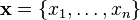
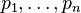
并代表该进程在点
[
我们举个例子δ函数是如何在量子力学权宜。
δ这里指的是克罗内克δ。
同 

这里的特征值被假定为离散的,但一个观察到的特征值的组,可以是连续的,而不是离散。
本征函数的位置表示 

即,φy是向量的
在分布意义上说,那么对于任何测试函数ψ,
哪里
即,作为在离散的情况下,有一个分辨率的身份
算子值的积分再次理解意识的淡薄。
δ函数在量子力学中,如三角洲潜在的单,双势阱模型,也有很多更专业的应用。
[
此外,作用于电子束的点的时刻可以通过delta函数描述。
[
凌动(测度理论)
从根本上解决
格林函数
Dirac测度
三角洲潜在
[
^
^
^
^
卡茨,米哈伊尔·
^
^
^
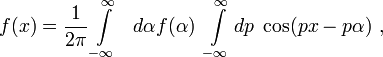

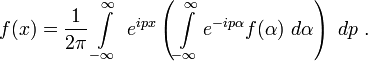
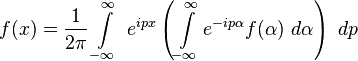
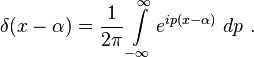
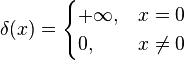




![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 H(X)= \ int_ {\ mathbb {R}} \ mathbf {1} _ {( - \ infty的,X]}(吨)\,\三角\ {DT \} = \三角洲( - \ infty的,X 。](http://upload.wikimedia.org/math/5/1/1/511aa34f5a3b146f582aa65d29188ce3.png)

![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \三角\ varphi] = \ varphi(0)\](http://upload.wikimedia.org/math/b/1/c/b1c2074d920e293f6ee23fc02130a233.png)
![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 | S [\披] | \乐C_N \ sum_ {k = 0} ^ {M_N} \ sup_ {X \ [-N,N]} | \披^ {(K)}(X)。](http://upload.wikimedia.org/math/0/3/0/030ace79cd564b4f45e9d7083e118018.png)
![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \三角\ PHI] = - \ int_ { - \ infty的} ^ \ infty的\披'(x)H(X)\,dx的。](http://upload.wikimedia.org/math/4/9/c/49c836b66863ded1069bba1f2c224c2c.png)




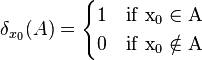
![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \ delta_ {X_0} [\披] = \岛(X_0)](http://upload.wikimedia.org/math/1/e/b/1eb3281ef2f90360471468f213e873b4.png)

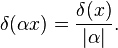

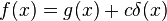
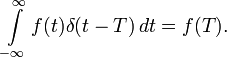
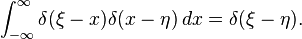



![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \δ(x ^ 2 - \阿尔法^ 2)= \压裂{1} {2 | \阿尔法|} [\三角洲(X + \α)+ \三角洲(X-\α)]。](http://upload.wikimedia.org/math/0/d/2/0d2927d0515a7f3f12a18d340aa7982e.png)


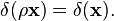

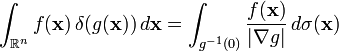

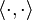





![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \ int_ { - \ infty的} ^ \ infty的E ^ {2 \ PI \ xi_1 T} \ [E ^ {I 2 \ PI \ xi_2 T} \] ^ * \,DT = \ int_ { - \ infty的} ^ \ infty的E ^ {-2 \ PI(\ xi_2 - \ xi_1)T} \,DT = \三角洲(\ xi_1 - \ xi_2)。](http://upload.wikimedia.org/math/d/6/8/d68f7cefb61fc55c5e9c8a558bfd9b95.png)
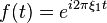

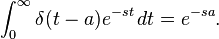
![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \三角洲“[\ varphi] = - \三角\ varphi'] = - \ varphi(0)。](http://upload.wikimedia.org/math/4/7/1/471945b0e4a22d140cb57d2852cb7469.png)

![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \δ^ {(十一)} [\ varphi] =(-1)^ K \ varphi ^ {(k)}的(0)。](http://upload.wikimedia.org/math/3/4/0/340c88866e5e9644a083eb073f44da09.png)

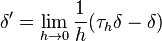
![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 (\ tau_h S)[\ varphi] = S [\ tau_ {小时} \ varphi]。](http://upload.wikimedia.org/math/5/8/2/582370f779f7278f90c4edd8dd1b2632.png)



![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \ delta_a [] = \ \披披岛(一)](http://upload.wikimedia.org/math/0/6/f/06f5bf5d607c7c7cd5b4a20cb5a935be.png)



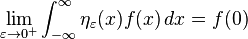

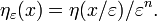
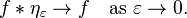






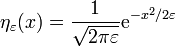
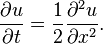



= | 2 \ PI \十一\ mathcal {F}( \十一)。](http://upload.wikimedia.org/math/7/3/5/73515d9c0dc273cdde7aea8a57f1d4a6.png)
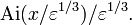

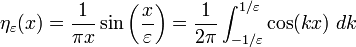
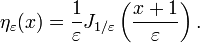
![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 L [U] = F,\,](http://upload.wikimedia.org/math/1/8/9/1892330c3bf4359ba7d85f5477cd1dc5.png)
![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 L [U] = \三角\](http://upload.wikimedia.org/math/5/b/9/5b90740ee993fff2fc4ab43ea58ea0f5.png)
![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 L [U] = H \](http://upload.wikimedia.org/math/d/5/4/d5479eae1f42c7bce59de2431206a266.png)

![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 G(S)= \ operatorname {RE} \左\压裂{-S ^ K \ LOG(是)} {(2 \ PI I)^ N} \] = \ {情况下,} \压裂K! {| S | ^ K表} {4K!(2 \ PI我)^ {N-1}}&ñ\文本{奇} \ \&\ \ - \压裂{|小号| ^ K表\日志| S |} { K!(2 \ PI I)^ {n}}&N \ {偶数。} \完{情况下}](http://upload.wikimedia.org/math/d/a/f/daf762b8ac926ae73edf7d238bab1787.png)
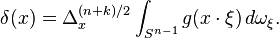

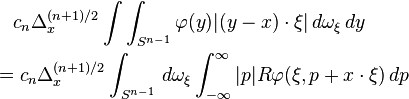

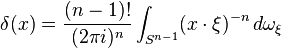

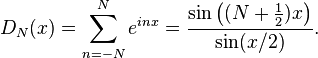


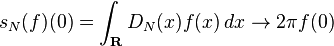




![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \三角洲[F] = F(0)| <C \ | F \ | _ {H ^ 1}。](http://upload.wikimedia.org/math/d/0/4/d041f4205de07df754884b550badb5ba.png)

![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \ delta_z [F] = F(Z)= \压裂{1} {2 \ PI I} \ oint_ {\部分D} \压裂{F(\泽塔)\ D \泽塔} {\泽塔-Z}。](http://upload.wikimedia.org/math/b/7/9/b791831a2283ea47b3ee2a7a27ecea0e.png)
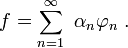
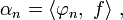
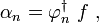

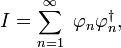
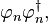





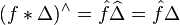
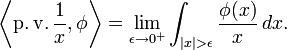
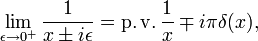
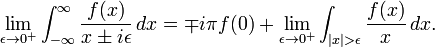
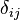




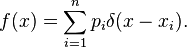


![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \埃尔(所述吨)= \ lim_ {\小量\为0 ^ +} \压裂{1} {2 \小量} \ INT_0 ^吨\ mathbf {1} _ {[所述的\小量,所述+ \ EPSILON] (S)}(B)\,DS](http://upload.wikimedia.org/math/4/c/4/4c48155188fb2350e808d7f8fe514e1d.png)
![狄拉克未函数Dirac <wbr>delta <wbr>function股票数学模型对冲基金方法 \ mathbf {1} _ {[X-\小量,X + \ EPSILON]}](http://upload.wikimedia.org/math/1/b/2/1b2a7c6077e38d4ec2070daf99a5d7ce.png)












No comments:
Post a Comment