2. 維基百科線上數學百科全書,CramersRule,http://mathworld.wolfram.com/CramersRule.html。
3. 蔡聰明,從醉月湖的面積談起,
http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/index.html。
4. 林琦焜,Green 定理與應用,http://episte.math.ntu.edu.tw/articles/mm/mm_21_4_03/index.html。
5. 笛卡爾之夢,九章出版社,P.267。
6. From Pythagoras to Grassmann,畢氏定理高維方面的推廣,傳播季刊第47 期。
|
從醉月湖的面積談起
向量微積分簡介 (第 3 頁) 蔡聰明
| |
.原載於數學傳播第二十一卷第二期
.作者當時任教於台大數學系
‧對外搜尋關鍵字 |
| |
公式(5)更是活生生的,它還可以再推廣,無窮化與連續化成平面上封閉曲線所圍成的領域(如醉月湖)之面積公式。為此,我們根據行列式的性質將(5)式稍作變形
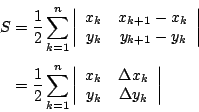 | (6) |
如何連續化呢?由微積分我們知道,圓內接正 n 邊形的連續化(即 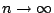 )就得到圓,差和分的連續化就是微積分,參見[3]。按此理,平面上封閉曲線 Γ 所圍成的領域,可以看作是邊長為無窮小 (infinitesimal) 的無窮多邊之多邊形(我們採無窮小論證之觀點)。所謂「連續化」在作法上就是將 和分 Σ 改為積分 )就得到圓,差和分的連續化就是微積分,參見[3]。按此理,平面上封閉曲線 Γ 所圍成的領域,可以看作是邊長為無窮小 (infinitesimal) 的無窮多邊之多邊形(我們採無窮小論證之觀點)。所謂「連續化」在作法上就是將 和分 Σ 改為積分 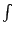
差分 Δ 改為微分 d 因此,(5)式的連續化就變成
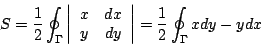 | (7) |
此地積分記號 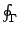 意指沿 Γ 以逆時針方向作曲線積分 (line integral)。我們可以這樣來理解(6)式:想像封閉曲線 Γ 上無窮地接近的兩點 (x,y)、(x+dx,y+dy) 與原點 (0,0) 所圍成無窮小的三角形面積為 意指沿 Γ 以逆時針方向作曲線積分 (line integral)。我們可以這樣來理解(6)式:想像封閉曲線 Γ 上無窮地接近的兩點 (x,y)、(x+dx,y+dy) 與原點 (0,0) 所圍成無窮小的三角形面積為
再讓 (x,y) 沿曲線 Γ 的逆時針方向變動,連續地求和(即積分),就得到(7)式,參見圖6。

圖6 |
- 例1:
- 橢圓 Γ 的參數方程式為
由(7)式算得
這恰是通常熟悉的橢圓面積公式。
因此我們很有理由相信公式(7)是對的。事實上,我們可以採用一般微積分教科書上的極限論證法給予證明。不過,我們要指明:從 Leibniz 或非標準分析 (non-standard analysis) 的眼光來看,無窮小論證法是合法的(歷史上曾被宣佈為「非法的」),更漂亮而具有發現的潛力,並且足以保證(7)式是成立的。
- 定理2:
- 設
![$\Gamma:t\in [a,b]\rightarrow(x(t)$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img27.gif) , , 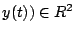 為一條單純的(即沒有打結)、封閉的可微分曲線,並且是逆時針定向,則 Γ 所圍成的領域之面積為 為一條單純的(即沒有打結)、封閉的可微分曲線,並且是逆時針定向,則 Γ 所圍成的領域之面積為
- 註:
- (8)式表示,沿著曲線 Γ 繞一圈,作某種功(或度量),就知道曲線所圍的面積,這真奇妙。一位農夫沿著農地走一圈就知道面積!
對於極坐標描述的封閉曲線 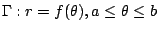 可改為參數方程式 可改為參數方程式
計算
於是得到:
- 推論:
- 設
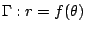 , , 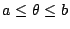 , 為一條單純的、封閉的可微分極坐標曲線,則 Γ 所圍成領域之面積為 , 為一條單純的、封閉的可微分極坐標曲線,則 Γ 所圍成領域之面積為
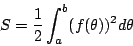 | (9) |
- 註:
- 事實上,不必限於封閉的極坐標曲線,(9)式亦成立。這是在微積分中我們熟悉的一個公式。
- 例2:
- 設 a>0,考慮半徑為 a 的圓在半徑為 3a 的圓內部沿著圓周滾動,試求滾動圓上一點 P 的軌跡所圍成領域之面積。
- 解:
- 如圖7所示,取圓心為原點,並且小圓上的 P 點起先跟 (3a,0) 點重合,然後開始滾動,再取圓心角 θ 當參數,容易算出 P 點的坐標 (x,y) 滿足
我們稱 P 點的軌跡為圓內三尖輪迴線 (Deltoid)。由公式(8)知,它所圍成領域之面積為
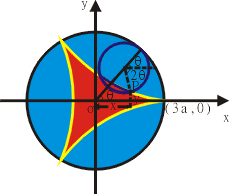
圖7 |
- 習題:
- 求星形線
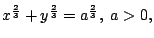 所圍的面積。 所圍的面積。
從醉月湖的面積談起
向量微積分簡介 (第 2 頁) 蔡聰明
| |
.原載於數學傳播第二十一卷第二期
.作者當時任教於台大數學系
‧對外搜尋關鍵字 |
| |
多邊形仍然太複雜,我們再退到三角形的特例,探尋完成後,再進到多邊形。這種處理問題時退、進之道很值得留意。
- 問題3:
- 已知三角形三個頂點的坐標為 A= (x1, y1), B = (x2, y2), C = (x3, y3), 如何求其面積?
我們進一步退到三個頂點為 O=(0,0), B=(x2, y2), C=(x3, y3) 之更特殊三角形。令 OB, OC 與 x 軸的夾角分別為 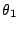 與 與 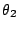 ,且 ,且 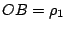 , , 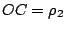 ,則 ,則
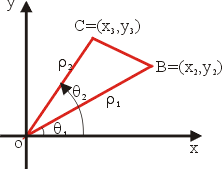
圖3 |
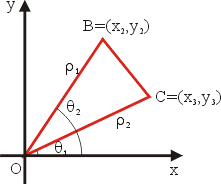
圖4 |
如上圖所示,我們分成兩種情形來討論: (i)當 O,B,C 成為逆時針(或右手系)定向時,如圖3,則 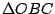 的面積為 的面積為
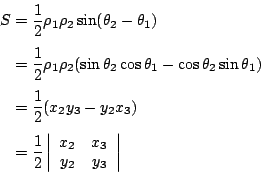 | (2) |
(ii)當 O,B,C 成為順時針(或左手系)定向時,如圖4,則 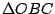 的面積為 的面積為
因此行列式
代表由 OB 與 OC 所生成的平行四邊形的有號面積,當 O,B,C 逆時針定向時為正,順時針定向時為負。利用向量外積也可以推導出這個結果。 回到問題3,不妨假設 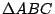 為逆時針走向,見圖5,則 為逆時針走向,見圖5,則 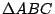 的面積為 的面積為
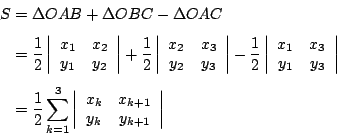 | (3) |
其中規定 x4=x1 且 y4=y1
- 註:
- 通常教科書將(3)式寫成
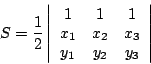 | (4) |
不過,(3)式適於推廣到任何多邊形,而(4)式則不然。換言之,(4)式是死的,(3)式才是活的有源之泉。
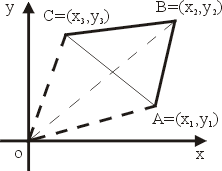
圖5 |
仿上述之論證可得
- 定理1:
- 設 A1 (x1 , y1) , A2 (x2 , y2) , … , An (xn,yn) 為 n 邊形之頂點坐標且為逆時針定向,則此 n 邊形的面積為
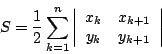 | (5) |
其中規定 xn+1=x1 且 yn+1=y1
- 註:
- (5)式又叫做測量師的公式。
| |
面積是一個很古老的幾何概念,它起源於人類要丈量土地的大小。Geometry 這個字的根源是 geometrein,geo 是土地,metrein 是測量,故幾何學的原意是測量土地、求面積。自古以來,由於所給的條件有各式各樣,於是對應有各式各樣的面積公式。經過兩千多年的發展,終於創立微積分,透過微分法一舉解決了一切求積問題。
- 問題1:
- 在平面上,一條封閉曲線所圍成的領域,例如台大的醉月湖,如何求它的面積呢?
按思考的常理,我們先退到比較簡單的特例,譬如說透過離散化或有窮化,退到多邊形,再退到四邊形乃至三角形。 對於三角形的情形,如果所給的數據是三個邊之長,那麼其面積就有 Heron 公式可循,參見 [1]。推廣到四邊形的情形,如果所給的數據是四個邊之長加上兩對角線或兩個對角,那麼其面積又有 Brahmagupta 公式與 Bretschneider 公式可算,參見 [2]。四邊形的面積公式已經有點煩瑣,如果要再推廣到五邊以上的多邊形,其困難是可以想像得到的,甚至根本行不通。一個求面積公式,若只能對付三角形或四邊形,那麼也太局限了,不合數學追尋普遍的“萬人敵”之道。 換個追尋的方向,改變所給的數據是個好辦法: (i)假設多邊形的頂點皆為平面上的格子點,那麼其面積就有 Pick 公式
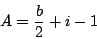 | (1) |
其中 b 與 i 分別表示在邊界上及內部的格子點之個數,參見[4]。讓格子的間隔越來越小,原則上利用(1)式可以求出一般平面領域的面積。 (ii)已知多邊形的頂點坐標,因為頂點唯一決定多邊形(邊則不然),所以多邊形的面積理應可以利用頂點的坐標來表達。 實際測量一塊多邊形的土地,我們得到邊長 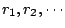 以及邊相對於水平線之旋轉角 以及邊相對於水平線之旋轉角 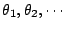 ,參見圖1。由這些數據可以得到多邊形的頂點坐標。設第一點的坐標為 A = (x1, y1) (由取平面坐標系而決定下來);然後就可求出 B = (x2, y2) 如下: ,參見圖1。由這些數據可以得到多邊形的頂點坐標。設第一點的坐標為 A = (x1, y1) (由取平面坐標系而決定下來);然後就可求出 B = (x2, y2) 如下:
接著求出 C=(x3,y3) 為
… 等等,參見圖2。
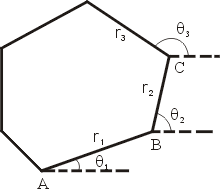
圖1 |
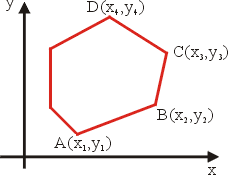
圖2 |
- 問題2:
- 已知多邊形的頂點坐標為 (x1,y1) , (x2,y2) , … , (xn,yn),如何求其面積?
本文的主題是:先追尋多邊形的面積公式;接著連續化得到平面上一般領域(包括醉月湖)的面積公式;再作推廣,得到平面上的 Green 定理;最後推廣到三維空間,得到 Gauss 的散度定理與 Stokes 的旋度定理。這些深深觸及向量微積分的核心,是一條值得探尋的路徑。 |
|
|
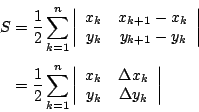

![\begin{eqnarray*}
S&=&{1\over 2}\oint_\Gamma xdy-ydx\\
&=&{1\over 2}\int_{0}^{...
...(-a\sin t)]dt\\
&=&{1\over 2}ab\int_{0}^{2\pi}dt\\
&=&\pi ab
\end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img26.gif)
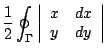
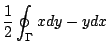
![$\displaystyle {1\over 2}\,\int_{a}^{b}[x(t)y'(t)\,-y(t)x'(t)]dt$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img31.gif)
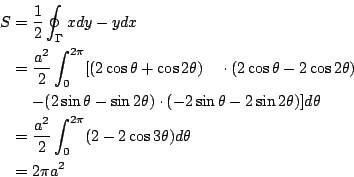

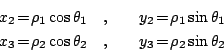


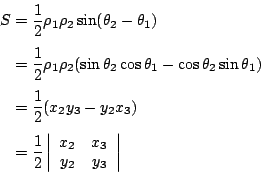
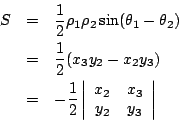
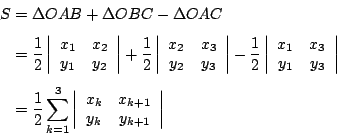
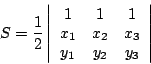

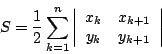


No comments:
Post a Comment