| |
公式(8)是露出海面上的冰山之一角,底下還有更廣大的整座冰山。為了發現這座冰山,我們將(8)式重新整理成:
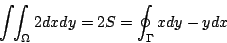 | (10) |
其中 Ω 表示 Γ 所圍成的領域,通常也記 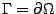 ,表示 Ω 的邊界。 (10)式顯示兩重積分與線積分具有密切關係。常函數 ,表示 Ω 的邊界。 (10)式顯示兩重積分與線積分具有密切關係。常函數  在 Ω 的內部作兩重積分就等於向量場 在 Ω 的內部作兩重積分就等於向量場 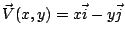 沿 Ω 的邊界 沿 Ω 的邊界 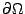 作線積分。這條線索類似於微積分根本定理 作線積分。這條線索類似於微積分根本定理
亦即 f 在邊界 ![$\partial[a,b]$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img47.gif) 上作積分(得 f(b)-f(a))等於 f 的變化率 f' 在 [a,b] 上作積分。因此,常函數 上作積分(得 f(b)-f(a))等於 f 的變化率 f' 在 [a,b] 上作積分。因此,常函數  似乎應該就是向量場 似乎應該就是向量場 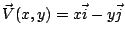 的某種「變化率」(或「微分」)。 的某種「變化率」(或「微分」)。
http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/page4.html
|
從醉月湖的面積談起
向量微積分簡介 (第 4 頁) 蔡聰明
| |
.原載於數學傳播第二十一卷第二期
.作者當時任教於台大數學系
‧對外搜尋關鍵字 |
| |
公式(8)是露出海面上的冰山之一角,底下還有更廣大的整座冰山。為了發現這座冰山,我們將(8)式重新整理成:
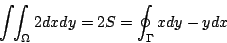 | (10) |
其中 Ω 表示 Γ 所圍成的領域,通常也記 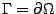 ,表示 Ω 的邊界。 (10)式顯示兩重積分與線積分具有密切關係。常函數 ,表示 Ω 的邊界。 (10)式顯示兩重積分與線積分具有密切關係。常函數  在 Ω 的內部作兩重積分就等於向量場 在 Ω 的內部作兩重積分就等於向量場 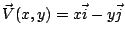 沿 Ω 的邊界 沿 Ω 的邊界 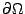 作線積分。這條線索類似於微積分根本定理 作線積分。這條線索類似於微積分根本定理
亦即 f 在邊界 ![$\partial[a,b]$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img47.gif) 上作積分(得 f(b)-f(a))等於 f 的變化率 f' 在 [a,b] 上作積分。因此,常函數 上作積分(得 f(b)-f(a))等於 f 的變化率 f' 在 [a,b] 上作積分。因此,常函數  似乎應該就是向量場 似乎應該就是向量場 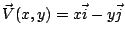 的某種「變化率」(或「微分」)。 為了尋找兩重積分與線積分的一般關係式,我們考慮平面上的向量場 的某種「變化率」(或「微分」)。 為了尋找兩重積分與線積分的一般關係式,我們考慮平面上的向量場
沿著一條封閉曲線 Γ 作線積分
- 問題4:
- 線積分
 可化成 Ω 上什麼形式之兩重積分,包括(10)式為特例? 可化成 Ω 上什麼形式之兩重積分,包括(10)式為特例?
我們仔細觀察(10)式。欲 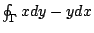 改寫成 改寫成  之形,只需取 之形,只需取
就好了。但是 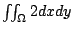 這一項怎麼來的呢?容易看出 這一項怎麼來的呢?容易看出
因此 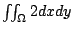 就是由 就是由 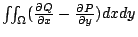 得來的。 到此為止,我們已經可以提出猜測(Conjecture): 得來的。 到此為止,我們已經可以提出猜測(Conjecture):
 | (11) |
我們先用一個例子來檢驗(11)式。
- 例3:
- 設
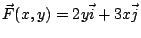 ,即 P(x,y) = 2y , ,即 P(x,y) = 2y , 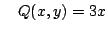 , , 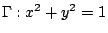 為單位圓,取參數方程式 為單位圓,取參數方程式
則
另一方面
因此,上述猜測對於本例成立。
我們已有相當理由支持(11)式之猜測,那麼我們就試證看看吧。 仍然從最簡單的情形著手: (i)當 ![$\Omega=[a,b]\times[c,d]$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img63.gif) 為矩形領域時,參見圖8。 為矩形領域時,參見圖8。
由 Newton-Leibniz 公式(簡稱 N-L 公式)知
所以

圖8 |
(ii)其次考慮平面領域 Ω,滿足:邊界  跟平行於 x 軸與 y 軸的直線至多只交於兩點,參見圖9。 跟平行於 x 軸與 y 軸的直線至多只交於兩點,參見圖9。
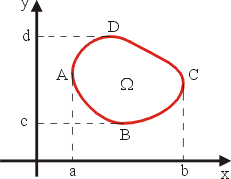
圖9 |
我們只需要證明
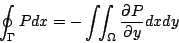 | (12) |
與
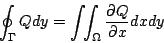 | (13) |
再相加起來就好了。今證(12)式:邊界 Γ 可以分成兩部分
 與 與 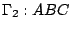 分別由函數 分別由函數
y=f1(x) 與 y=f2(x), ![$x \in [a,b]$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img71.gif) 所定義,於是 所定義,於是
同理可證明(13)式。 (iii)當 Ω 為單純連通領域 (simply connected region) 時,可以分割成幾個(ii)的領域之聯集,這種情形上述的猜測也成立。參見圖10。
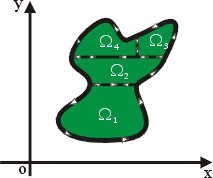
圖10 |
- 定理3:(Green 定理,1828年)
- 設 Ω 為由封閉曲線 Γ 所圍成的單純連通領域,並且 P , Q ,
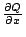 , , 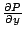 在 Ω 上皆為連續函數,則 在 Ω 上皆為連續函數,則
 | (14) |
- 註:
- 我們不去追求最廣泛的 Green 定理。 一般微積分教科書都將(10)式貶為是(14)式的特例或腳註。我們反其道而行, 將(10)式視為是生出(14)式的胚芽 (germ) 或線索 (clue)。
| |
從醉月湖的面積談起
向量微積分簡介 (第 5 頁) 蔡聰明
| |
.原載於數學傳播第二十一卷第二期
.作者當時任教於台大數學系
‧對外搜尋關鍵字 |
| |
如何將 Green 定理推廣到三維空間?為此,我們要對於 Green 定理的形式與內涵兩方面作更詳細的考察。 | | |
| |
Green 定理可以寫成兩個等價的形式:
 | (15) |
 | (16) |
事實上,在(15)式中,將 P 改為 -Q,Q 改為 P,就得到(16)式;反過來,在(16)式中,將 P 改為 Q,Q 改為 -P,就得到(15)式。 進一步,採用向量記號將(15)與(16)改寫: 令向量場  , 及微分算子 , 及微分算子 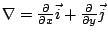 。 模仿向量的內積與外積運算,我們定義: 。 模仿向量的內積與外積運算,我們定義:
再令 s 表示曲線 Γ 之弧長參數,ds 表示無窮小線元,於是單位切向量為
向外單位法向量為
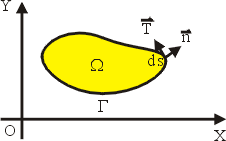
圖11 |
參看圖11。於是
以及
從而(15), (16)兩式可分別改寫成:
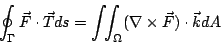 | (19) |
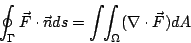 | (20) |
其中 dA 表示無窮小的面積元。(19)式叫做切向式(tangential form),(20)式叫做法向式(normal form)。換言之,Green 定理有(15)、(16)、(19)與(20)四種化身。這四個式子都叫做 Green 公式。 | | |
| |
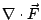 與 與 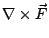 (即(17)與(18)兩式)代表什麼物理意義呢? 由於 Green 公式與 N-L 公式在形式與內涵上都具有相同的本質,所以 (即(17)與(18)兩式)代表什麼物理意義呢? 由於 Green 公式與 N-L 公式在形式與內涵上都具有相同的本質,所以 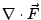 、 、 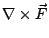 與函數 f' 應該具有密切關連。 與函數 f' 應該具有密切關連。
- 問題5:
- 如何解釋 N-L 公式
我們採用流體流動的觀點來解釋。考慮一根直線管子,參見圖12,假設橫截面具有單位面積。

圖12 |
今想像有流體在管子中流動,其速度場為 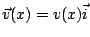 ,密度為 ,密度為 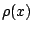 。令向量場 。令向量場
這叫做流體的通量向量場 (the flux vector field of the flow)。因此,f(x) 表示單位時間流體通過 x 點處橫截面之通量 (flux)。由於 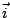 是向右之單位向量,故當 f(x)>0 時,表示流體向右流過 x 點處的截面;當 f(x)<0 時,表示流體向左流過 x 點處的截面。於是從大域的 (global) 眼光來看,f(b)-f(a) 表示在管段 [a,b] 中,單位時間流體的減少量,即單位時間流體流出 [a,b] 的通量。 另一方面,從局部的 (local) 眼光來看流速場的變化。考慮區間 是向右之單位向量,故當 f(x)>0 時,表示流體向右流過 x 點處的截面;當 f(x)<0 時,表示流體向左流過 x 點處的截面。於是從大域的 (global) 眼光來看,f(b)-f(a) 表示在管段 [a,b] 中,單位時間流體的減少量,即單位時間流體流出 [a,b] 的通量。 另一方面,從局部的 (local) 眼光來看流速場的變化。考慮區間 ![$[\alpha,\beta] \subset[a,b]$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img100.gif) 且 且 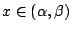 ,那麼 ,那麼 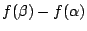 表示在管段 表示在管段 ![$[\alpha,\beta]$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img103.gif) 中單位時間流體的減少量,從而,牛頓商 中單位時間流體的減少量,從而,牛頓商  表示單位時間單位長度管段 表示單位時間單位長度管段 ![$[\alpha,\beta]$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img103.gif) 中流體的平均減少量。因此微分 中流體的平均減少量。因此微分
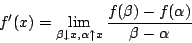 | (21) |
表示單位時間單位長度流體在 x 點處的減少量,亦即在 x 點單位時間單位長度流散出的量,因此叫做散度 (divergence)。按積分的定義可知, 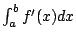 表示單位時間流體在 [a,b] 中的減少量。今因流體不會無中生有,也不會無故消失,所以 N-L 公式 表示單位時間流體在 [a,b] 中的減少量。今因流體不會無中生有,也不會無故消失,所以 N-L 公式
顯然成立。這是一種散度定理。 上述流體的觀點,推廣到兩維平面恰好也就是 Green 定理(20)式的解釋。為了說明這件事,我們必須推廣(21)式。 在(21)式中,分母可改為矩形的面積,但是分子較難推廣,不過並不絕望。我們重新整頓一下  :分母是區間 :分母是區間 ![$I=[\alpha,\beta]$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img108.gif) 的長度,記為 |I|,而分子 的長度,記為 |I|,而分子 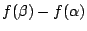 改為 改為
其中  是 I 的邊界點,符號 (-1)i 表示在左端點取負號,右端點取正號,這樣才符合流體流出 是 I 的邊界點,符號 (-1)i 表示在左端點取負號,右端點取正號,這樣才符合流體流出 ![$I=[\alpha,\beta]$](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img108.gif) 的意思,即在 I 的端點流體是向外流出的。換言之,在邊界點都賦予向外法向之概念,即 的意思,即在 I 的端點流體是向外流出的。換言之,在邊界點都賦予向外法向之概念,即
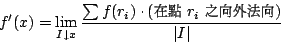 | (22) |
其中 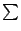 是對 I 的邊界點來求和的。經過這樣的修飾,(22)式才適合推廣到高維空間。 設 是對 I 的邊界點來求和的。經過這樣的修飾,(22)式才適合推廣到高維空間。 設  為兩維平面上的一個向量場,想像成流體的通量向量場。令 為兩維平面上的一個向量場,想像成流體的通量向量場。令  為平面上一塊領域, 為平面上一塊領域,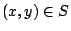 ,將(22)式中的求和 ,將(22)式中的求和 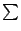 改為沿邊界 改為沿邊界 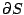 作積分,即定義: 作積分,即定義:
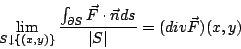 | (23) |
叫做向量場 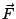 在 (x,y) 點的散度 (divergence),其中 |S| 表示 S 的面積, 在 (x,y) 點的散度 (divergence),其中 |S| 表示 S 的面積,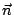 表示沿邊界的 表示沿邊界的 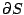 的向外單位向量。這是一維導數(22)式的類推與推廣。 根據定義, 的向外單位向量。這是一維導數(22)式的類推與推廣。 根據定義, 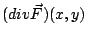 代表在 (x,y) 點處單位時間單位面積流體向外流出的通量。這是局部變化率,是向量場 代表在 (x,y) 點處單位時間單位面積流體向外流出的通量。這是局部變化率,是向量場 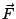 的一種「微分」概念。 的一種「微分」概念。
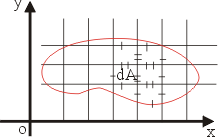
圖13 |
按兩重積分的定義, 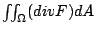 的意義是:將 Ω 分割成無窮多塊的無窮小塊,參見圖13。於是 的意義是:將 Ω 分割成無窮多塊的無窮小塊,參見圖13。於是 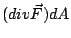 表示單位時間流體流出 dA 的通量,然後對整個 Ω 連續求和,即作積分,就得到 表示單位時間流體流出 dA 的通量,然後對整個 Ω 連續求和,即作積分,就得到 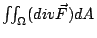 。由於在內部的邊界,流體的進出恰好抵消,整個合起來只剩下流出邊界 。由於在內部的邊界,流體的進出恰好抵消,整個合起來只剩下流出邊界 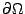 的通量。因此, 的通量。因此, 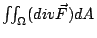 代表單位時間流體流出 代表單位時間流體流出 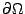 的通量。另一方面,這個流出通量按定義就是線積分 的通量。另一方面,這個流出通量按定義就是線積分 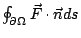 ,所以下式顯然成立: ,所以下式顯然成立:
 | (24) |
此式跟(20)式還有一段距離,不過我們可以證明
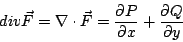 | (25) |
代入(24)式就得到法向式的 Green 公式了。 另一方面,在上述(23)式的定義中,其分子是沿邊界 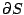 的向外單位法向作積分,現在如果改為沿邊界的切向 的向外單位法向作積分,現在如果改為沿邊界的切向  作積分,用循環量 (Circulation) 代替通量 (flux),就得到旋度 (Curl 或 rotation) 的定義: 作積分,用循環量 (Circulation) 代替通量 (flux),就得到旋度 (Curl 或 rotation) 的定義:
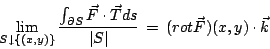 | (26) |
換言之, (有時也記為 (有時也記為  )為一個向量場,它在 z 軸的投影恰好就是流體在 (x,y) 點處單位時間單位面積的循環量。這也是局部變化率,是向量場 )為一個向量場,它在 z 軸的投影恰好就是流體在 (x,y) 點處單位時間單位面積的循環量。這也是局部變化率,是向量場 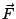 的另一種「微積分」概念。 的另一種「微積分」概念。
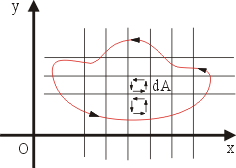
圖14 |
按重積分的定義,  的意義是: 將 Ω 分割成無窮多塊的無窮小塊,參見圖14。 於是 的意義是: 將 Ω 分割成無窮多塊的無窮小塊,參見圖14。 於是 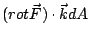 表示單位時間流體繞 dA 的循環量,然後對整個 Ω 作積分得到 表示單位時間流體繞 dA 的循環量,然後對整個 Ω 作積分得到  。由於沿內部的邊界之循環量恰好來回抵消, 整個合起來只剩下沿邊界 。由於沿內部的邊界之循環量恰好來回抵消, 整個合起來只剩下沿邊界 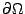 的循環量。另一方面,這個總循環量按定義就是線積分 的循環量。另一方面,這個總循環量按定義就是線積分 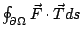 ,所以下式顯然成立: ,所以下式顯然成立:
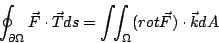 | (27) |
我們也可以證明
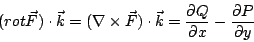 | (28) |
代入(27)式就得到切向式的 Green 公式了。
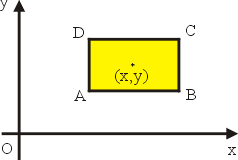
圖15 |
下面我們就來證明(25)與(28)兩式。 為了計算方便起見,我們作一矩形,以 (x,y) 點為中心,圍成領域 S,並且四邊跟 x 軸或 y 軸平行,參見圖15。設  ,於是四個頂點的坐標為 ,於是四個頂點的坐標為
我們先證明(25)式。為此,必須估算流體流出 S 之通量。流體流出邊界 AB, CD, AD 與 BC 的通量分別約為
其中我們取四邊的中點當估值的代表點。因此,流出 S 的通量約為
由平均變率定理 (Mean value theorem),這個通量為
![\begin{displaymath}[{\partial P\over\partial x}(x\!+\!\xi\Delta x,y) +
{\partial Q\over\partial y}(x,y+\eta\Delta y)] \Delta x \Delta y
\end{displaymath}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img139.gif) | (29) |
其中 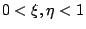 。顯然,當 。顯然,當  與 與 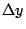 越來越小時,近似估計就越來越精確。 今將(29)式除以 越來越小時,近似估計就越來越精確。 今將(29)式除以  ,再讓 ,再讓  與 與 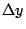 趨近於 0,則得 趨近於 0,則得
亦即
於是(25)式得證。 其次證明(28)式,仍然參見圖15。我們要估算流體沿邊界 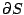 的循環量,即 的循環量,即 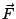 沿 AB、BC、CD、DA 的線積分,其總和約為 沿 AB、BC、CD、DA 的線積分,其總和約為
其中 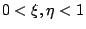 。 將(29)式除以 。 將(29)式除以  ,再讓 ,再讓  與 與 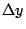 趨近於0,得到 趨近於0,得到
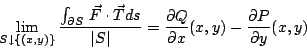
亦即
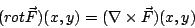
從而(28)式得證。
|
| 6. 推廣到三維空間:Gauss 定理與 Stokes 定理 |
抓住了 Green 公式的形式與內涵,要推廣到三維空間就不難了。首先令
表示空間中的一個向量場 (Vector field),即定義在空間中某領域的一個向量值函數。
- 定義:
分別叫做向量場 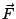 的散度與旋度。 的散度與旋度。
其次我們注意到,平面領域 Ω 可以有兩個方向的推廣:一個是空間中的可定向 (Orientable) 曲面 S(Möbius帶子就不是可定向曲面),參見圖16;另一個是空間中的一塊立體領域 V,參見圖17。
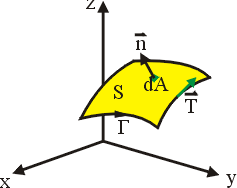
圖16 |
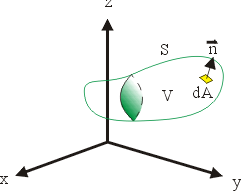
圖17 |
在(19)式中,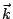 是 Ω 的向外單位法向量;當 Ω 改為空間曲面 S 時, 是 Ω 的向外單位法向量;當 Ω 改為空間曲面 S 時,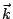 就應該改為 S 的向外單位向量 就應該改為 S 的向外單位向量 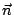 。 我們可以證明 。 我們可以證明 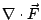 與 與 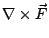 跟二維的情形有類似的解釋。 跟二維的情形有類似的解釋。 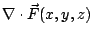 表示單位時間單位體積流體在點 表示單位時間單位體積流體在點 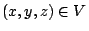 的流出通量, 的流出通量, 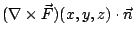 表示單位時間單位體積流體在點 表示單位時間單位體積流體在點  的循環量。從而(19)與(20)兩式就推廣為: 的循環量。從而(19)與(20)兩式就推廣為:
- 定理4: (Gauss 定理,又叫做散度定理,1839年)
- 設向量場
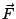 的分量 P,Q,R 及其一階偏導函數皆為連續函數,則 的分量 P,Q,R 及其一階偏導函數皆為連續函數,則
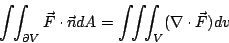 | (31) |
其中 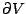 為圍成 V 之封閉曲面,dV 表示無窮小的體積元。 為圍成 V 之封閉曲面,dV 表示無窮小的體積元。
- 定理5: (Stokes 定理,又叫做旋度定理,1854年)
- 在與定理4相同的假設下,我們有
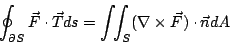 | (32) |
參見圖16。
在上述中,(31)式與(32)式分別將曲面積分與三重積分,線積分與曲面積分連結起來。若採用直角坐標系來表達,它們分別就是
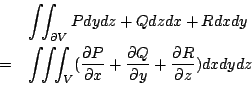
以及
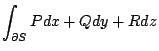 | = | 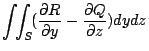 | |
| | + | 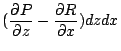 | |
| | + | 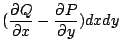 | (33)
|
從醉月湖的面積談起
向量微積分簡介 (第 7 頁) 蔡聰明
| |
.原載於數學傳播第二十一卷第二期
.作者當時任教於台大數學系
‧對外搜尋關鍵字 |
| |
我們從醉月湖的求面積問題出發,先退到多邊形,再退到三角形,最後更退到一頂點是原點之特殊三角形。此時問題變得很簡單,一下子就解決了。然後開始前進,先是一般三角形,再來是多邊形,緊抓住公式的正確形式,連續化就解決了求醉月湖的面問題。接著順勢推舟,飛躍出 Green 定理,整理成法向式與切向式,再類推、推廣成三維空間的 Gauss 定理與 Stokes 定理,最後統合於廣義的 Stokes 定理。 這種解決問題的「退進之道」,在數學中隨處可見。偉大數學家 Hilbert 說得淋漓盡致:「做數學的要訣(或藝術)在於找到含有普遍性的所有胚芽那個特例。」 (The art of doing mathematics consists in finding that special case which contains all the germs of generality.) 三角形的面積公式就是符合 Hilbert 所說的「那個特例」。本文正好可作為 Hilbert 這句名言之腳註。 特殊孕育出普遍,充實普遍;普遍又回過頭來照顧特殊,含納特殊。這種特殊到普遍之拾級而上,有機連結,互相啟發與觀照,發人深省。
- 1.蔡聰明:談Heron公式──記一段教學經驗,數學傳播,第十七卷第一期,1993。
- 2.蔡聰明:四邊形的面積,數學傳播,第十七卷第三期,1993。
- 3.蔡聰明:Leibniz 如何想出微積分?數學傳播,第十八卷第三期,1994。
- 4. B. Grunbaum and G. C. Shephard, Pick's Theorem, Amer. Math. Monthly, 150-161, 1993.
- 5. M. J. Crowe, A History of Vector Analysis, Univ. of Notre Dame Press, 1967.
- 6. M. Kline, Mathematical thought from Ancient to modern time, Oxford Univ. Press, 1972.
- 7. D. M. Bressoud, Second year calculus, Springer-Verlag, 1991.
|
|
這一切可以再推廣到 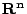 的可定向 k 維可微分子流形 的可定向 k 維可微分子流形  ,用微分式的積分與外微分理論,統合成為廣義的 Stokes 定理: ,用微分式的積分與外微分理論,統合成為廣義的 Stokes 定理:
 | (34) |
其中 ω 為 k-1 型微分式。這是微積分學根本定理最本質的形式。 |
|
|
|
![\begin{eqnarray*}
\int_{[a,b]} f'(x)dx &=& \int_{\partial[a,b]}f(x)dx \\
&=& f(b)-f(a)
\end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img46.gif)
![\begin{eqnarray*}
\int_{[a,b]} f'(x)dx &=& \int_{\partial[a,b]}f(x)dx \\
&=& f(b)-f(a)
\end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/img46.gif)
No comments:
Post a Comment