phymath999: 衍射分析中除了不能测定相位之外，还有衍射实验所得的强度（振幅或“幅度”）数据也是不完全的，只能得到部分衍射强度数据。所以从不完全的衍射强度做相位恢复的难度就更大了

所谓相位恢复，是依据傅立叶变换幅度，得出原图像的问题。X 射线衍射分析技术是分析材料分子结构的基本技术。可观测到的衍射（Bragg衍射）图样是一个二维函数傅里叶变换的幅度，测不到相位。这个幅度函数称为材料分子的结构因数，如果找到了它，通过富氏反变换就可能得到分子的电子密度函数，就是常说的分子结构。X射线分析技术的大量工作是搞（猜、估、推、试）一个方法来弥补相位。相位恢复是用数字图像处理方法，从傅立叶变换幅度，估计相位，得出原图像。虽然实际问题绝非描述的那样简单，由于此方法有可能给X 射线衍射分析技术带来革命性进步，研究人员仍然正在不懈努力中。

相位恢复问题还来源于天文图像处理。例如地基天文观测会受到大气层不均匀扰动的影响，犹如隔着紊乱皱褶玻璃看图像，并且还是时变的。有些观测处理方法能够较准确地估计目标图像傅里叶变换幅度，但得不到相位。

从70年代起，图像相位恢复成为图像处理领域中“最有兴趣和最富挑战性的问题之一”。一种迭代富氏变换方法被实践证明在许多情况下可行，但不总是可行。实践证明，如果对图像的支持域（图像象元值不为0的全体坐标点集合）有一个紧的估计，相位恢复的迭代算法会快速收敛到正确解。

支持域估计，是通过目标自相关支持域，估计目标支持域。因为傅里叶变换幅度已知，就能得到自相关。搞清自相关支持域和目标支持域的关系，就变得重要。自相关是原图像和它的（两个坐标的）翻转版本的卷积。对复杂图形，实施翻转、卷积操作会给研究者带来空间想像上的困难。利用“不卷”的卷积计算方法不仅计算上直观，而且很容易了解自相关支持域和目标支持域的关系，使支持域估计更容易把握。注意，x(m,n) 的自相关是 x(m,n)*x(-m,-n), 而不是别的。

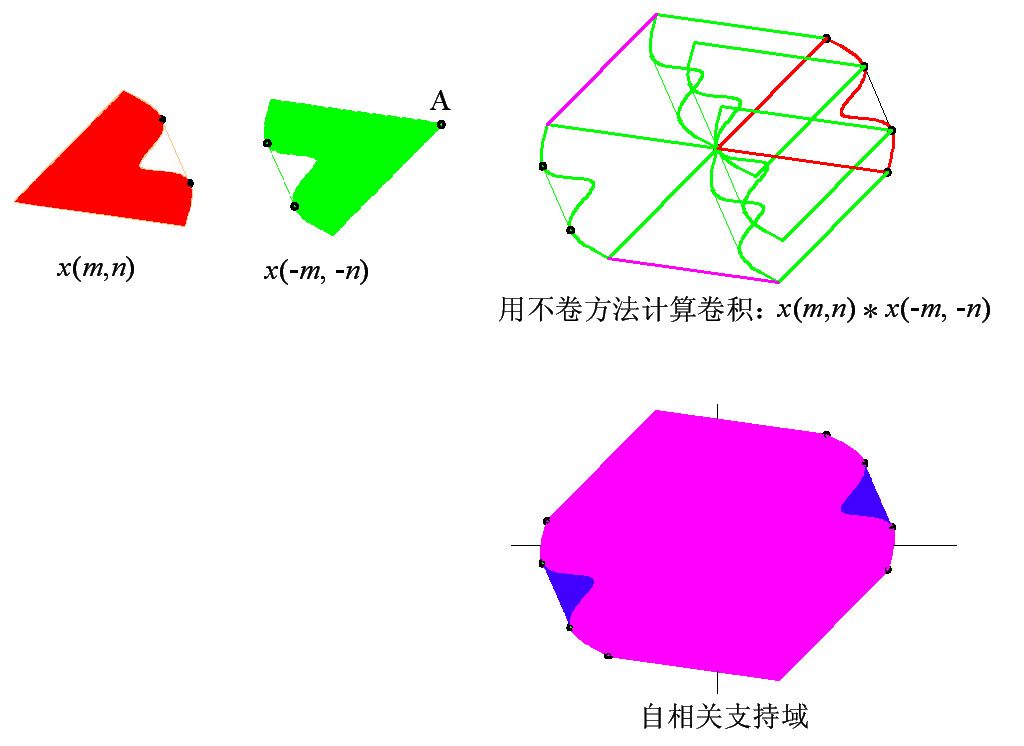
可以看出，（1）自相关支持的各个边是成对对称的，成对对称的两个边分别属于x(m,n) 或 x(-m,-n)。（2）因此按成对取一的方式划分自相关支持的各个边成为两个集合，每个集合应该形成一个封闭图形。

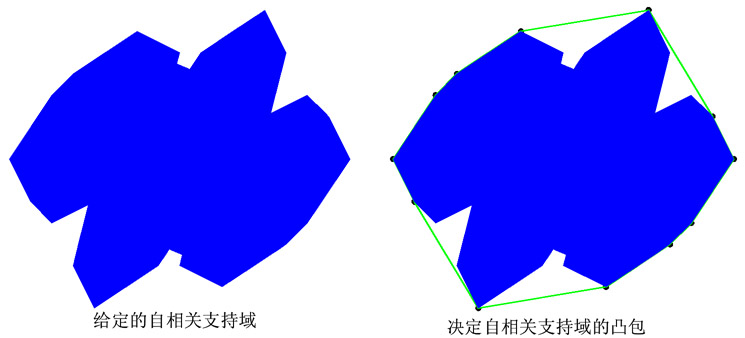
实际处理中的自相关支持常常非凸，须先构造一个包含它的紧的凸包，使具有自相关对称性。先分解凸包成为两个镜像对称的子凸包，它们中任何一个都是目标支持域凸包的估计。将子凸包与原凸包连带自相关支持，按边对边做图形的交运算，就得到目标支持域紧估计。

以下用图示方法描述如何获得目标支持的紧估计。

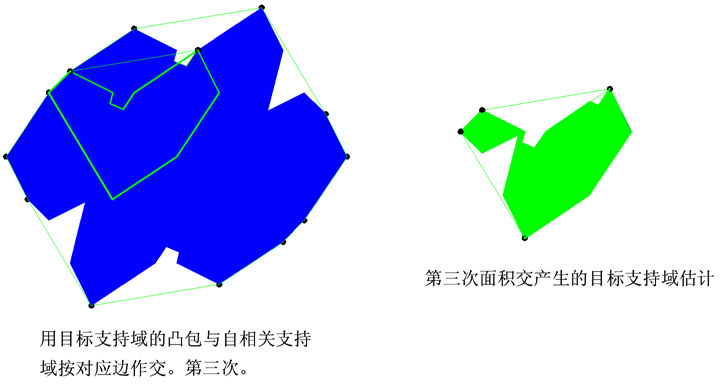
（材料来源于本人为中科院研究生院课程所作课件）

本文引用地址：http://blog.sciencenet.cn/blog-4909-429930.html
上一篇：研学小记：卷积不卷（3）――支持域计算和强制不可约多项式
下一篇：也议中科院

收藏分享举报

当前推荐数：7 推荐人：谢鑫 朱新亮 田灿荣 江万寿 tuner CyuSing vigorous

发表评论评论 (4 个评论)

[4]董成 2011-4-6 16:06: 衍射分析中除了不能测定相位之外，还有衍射实验所得的强度（振幅或“幅度”）数据也是不完全的，只能得到部分衍射强度数据。所以从不完全的衍射强度做相位恢复的难度就更大了。请问您所说的方法在这类问题中实际应用的效果如何？可以给出已经发表的有关参考文献吗？; 博主回复(2011-4-6 18:58)：这是1992-1994在德国做图像处理研究的工作，我本人没有做衍射分析的工作，只读过一些文献，在Journal of Optical Soci. of Amer.,(JOSA)上。迭代富氏变换是一种很灵活的方法，在迭代过程中可以把尽可能得到的先验知识加进去。因此，应该能容许部分幅度缺失。当然，可获得的知识越多越好。这种方法目前还没有进入应用，只是一种方法和理论可能性，值得有人去探索。可能需要跨学科的知识结合。

[3]董成 2011-4-6 10:47: “X 射线衍射分析技术是分析材料分子结构的基本技术。X 射线衍射分析技术是分析材料分子结构的基本技术。可观测到的衍射（Bragg衍射）图样是一个二维函数傅里叶变换的幅度，测不到相位。”
一般情况下都是用衍射技术来测定晶体的三维结构，观测到的单晶衍射也是三维的，而不是二维的。而多晶粉末衍射是通常只能观测到三维衍射在一维方向的投影。只有少数情况用二维探测器观测到的衍射是二维的，但实际对应的晶体结构通常仍然是三维的。; 博主回复(2011-4-6 15:52)：实际情况确实如你所说是三维的。但
（1）常常投影到若干个二维，可以减少计算量；
（2）这里介绍的相位恢复和支持域估计方法原则上可推广到三维，只是计算量更大。
（3）传统的一维估计方法可能需要大力改造。二维是比较现实的出路。二维和三维相位恢复的可能性（解的事实唯一性）隐含在“二变量或三变量多项式通常是不可分解的”这个事实上。

[2]tuner 2011-4-6 08:57: 好文！在X 射线衍射分析中使用傅里叶变换得到原图像的技术听说过，但没接触过。

[1]刘玉仙 2011-4-5 22:35: 是真不懂; 博主回复(2011-4-6 15:31)：先读“卷积不卷（3）”试试！

phymath999

Sunday, June 8, 2014

衍射分析中除了不能测定相位之外，还有衍射实验所得的强度（振幅或“幅度”）数据也是不完全的，只能得到部分衍射强度数据。所以从不完全的衍射强度做相位恢复的难度就更大了

布拉格衍射_百度百科

威廉·劳伦斯·布拉格- 维基百科，自由的百科全书

衍射- 维基百科，自由的百科全书

微波布拉格(Bragg)衍射

布拉格衍射及其应用

布拉格衍射公式- 功能材料- 小木虫- 学术科研第一站

声光bragg衍射的翻译结果 --cnki翻译助手

当前推荐数：7 推荐人：谢鑫 朱新亮 田灿荣 江万寿 tuner CyuSing vigorous

发表评论评论 (4 个评论)

No comments:

Post a Comment

Sunday, June 8, 2014

衍射分析中除了不能测定相位之外，还有衍射实验所得的强度（振幅或“幅度”）数据也是不完全的，只能得到部分衍射强度数据。所以从不完全的衍射强度做相位恢复的难度就更大了

当前推荐数：7 推荐人： 谢鑫 朱新亮 田灿荣 江万寿 tuner CyuSing vigorous

发表评论 评论 (4 个评论)

No comments:

Post a Comment

当前推荐数：7 推荐人：谢鑫朱新亮田灿荣江万寿 tuner CyuSing vigorous

发表评论评论 (4 个评论)