新人求科普，关于旋度与散度| 万物至理小组| 果壳网科技有意思
www.guokr.com/post/529176/
轉為繁體網頁
轉為繁體網頁
电磁场与电磁波1-2 - 百度文库
wenku.baidu.com/view/e2efa2274b35eefdc8d33345
轉為繁體網頁
轉為繁體網頁
旋度- 维基百科，自由的百科全书
zh.wikipedia.org/zh-hk/旋度
轉為繁體網頁
轉為繁體網頁
電勢- 维基百科，自由的百科全书
zh.wikipedia.org/zh-hk/電勢
[PPT]
一总电量为Q>0的金属球，在它附近P点产生的场强为 。 ... θ等于90度，即电场线顺着平面，通量为零；; θ大于90度，即电场线逆着法向穿过曲面，通量为 ... 即在静电场中，场强沿任意闭合路径的线积分恒等于零。 ... 静电场是保守场，静电场力是保守力.
第一章静电场.ppt - 西安电子科技大学
stp.xidian.edu.cn/jpkc/class/em/jiaoan/1.ppt
轉為繁體網頁
轉為繁體網頁
新人求科普，关于旋度与散度
LZ偶尔看到旋度这个新概念，好奇心奔涌而出，打开维基百科却大片大片的公式，推导映入眼球......所以，哪位大神可以解释一下旋度的物理概念（应该是和电磁场有关的吧），以及它的意义。
全部评论(7)
-
1楼 2013-11-16 19:35 fdsn 只看Ta[高中生没专业学过，出错不负责]顶 [0] 评论
wiki:（我只能看懂这些）
在三维直角坐标系Oxyz中，设向量场
为[2]:8：
其中的
，
分别是x轴、y轴、z轴方向上的单位向量，场的分量P、Q、R具有一阶连续偏导数， 那么在各个坐标上的投影分别为：
的向量叫做向量场A的旋度，也就是[1]:14：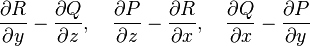
旋度的表达式可以用也行列式记号形式表示[2]:4-5：
需要注意的是这里的行列式记号只有形式上的意义，因为真正的行列式中的系数应该是数而不是
这样的向量。这种表示方法只是便于记忆旋度在直角坐标系中的表达式[3]。
感觉已经讲得很清楚了
物理意义：
（斯托克斯定理）当一个向量场的旋度是零时场为保守场，即闭合曲线上F点乘dl积分为零。物理上就是带着物体走一圈场做功为零，如重力场，电场（无磁通量变化） -
2楼 -
3楼 2013-11-17 11:37 呜呱星人老美的书里有一些比较直观的解释。可以去看看他们的新生微积分那类书。顶 [0] 评论
大致是什么意思呢，我也就是个初学者水平，话说的也不是特别清楚。不过我还是可以稍微说说。
想像一个游泳池。进水口在此，排水口在彼。
面积分说的是啥呢？面积分说的是绕着这个进水管画一个封闭曲面，楼主就想象成球面最简单。忽略进水口与排水口连接的水管，认为水在进水口凭空产生，在出水口凭空消失。那么从内向外（由外向内则反）流过这个曲面的水量就可以大致理解为面积分的值。
现在我们来看，假设我们这个曲面画的不囊括进出水口，且水不可压缩，那么流进这个曲面的水必须流出去。流进多少就流出多少，流出多少就流进多少。正负相加，这个面积分得零。（质量守恒定律）
以上是宏观解释，我们再来看微观的（此处微观与分子原子无关，我们假设水是连续的）
场与法向量点积的面积分等于散度的三重积分（高斯-奥斯特罗格拉兹基散度公式）。流体力学的连续性方程告诉我们，密度对时间的导数加上流率的散度等于零。现在水不可压缩，密度不变，那么流率的散度也就是零。求三重积分肯定还是零。也即，面积分等于零。
以上是不囊括进出水口的情况，我们再来讨论复杂一点的，曲面内部有且只有一个进水口的情况（出水口一样，就是正的变成负的）。宏观上看，有水从内向外流出这个曲面。（不要忘记我们假设水在进水口处是凭空产生的）也即面积分大于零
微观上看呢，在进水口处流率（这个词是我胡编乱造的，因为我根本没有系统的学过流体力学）的散度大于零，在别处流率的散度等于零。那么三重积分积下来（如果把进水口想象成点的话就要用到dirac的delta函数，比较麻烦。所以在这里我就只说个大概意思）是大于零的，也即流量的面积分大于零。
再想像曲面囊括两个口，一个排水一个进水。好了，宏观上，我们发现假设假设排水口有点堵的话，进水就比排水多，面积分为正，反之亦然。微观上呢，进水口的散度就比排水口的散度绝对值大，一积分一叠加你就发现三重积分是正的，于是乎向外净流量也是正的。
再想像，这回不是两个三个进出水口了，想像他们是连续分布的。道理差不多，这个曲面里的水盛不下了就要往外跑，曲面里的水太少别出的水就要补进来。这就是高斯-奥氏散度定理。 - 4楼 2013-11-17 11:50 呜呱星人 只看Ta现在我们再想像，不是一个曲面，而是两个有一部分共用的封闭曲面。（就假设一个椰子被切一刀，切成的两半套上保鲜膜，再和起来。两片保鲜膜重合在一起）我们现在来计算穿过曲面甲，曲面乙以及曲面甲乙的面积分。在“椰子壳”处一切好说，而再保鲜膜处就有意思了：曲面甲在曲面乙的外部，反之亦然。于是乎保鲜膜甲处的外法向和同一点上保鲜膜乙的外法向相反，而流率是一样的，于是乎在保鲜膜上的面积分甲乙互为相反数。（这很正常，流出甲的水流入乙）于是乎在曲面甲乙上的面积分等于椰子壳上的面积分，不论有没有保鲜膜。顶 [0] 评论
这样我们就可以把一个复杂的图形切割开，切割成简单的，无穷小的，然后把它们叠加起来求出整个积分，证明高斯-奥氏散度公式。 - 5楼 2013-11-17 12:12 呜呱星人 只看Ta我们再来看stokes公式。思路是差不多的，只不过这里都是伪向量。泡利的讲义有那么一段讲得还可以，就是张量拿过来就用我有点吓一跳。顶 [0] 评论
我们这次来想象一下。。龙卷风。美国人民表示这玩意破坏力还是挺强的。这里的龙卷风呢，可以有各种不同的形状，方圆均可。风的每一点对应着一个力，这个力会对在这一点上运动的物体做功。（至于为什么小物件非要跟着龙卷风的形状走呢。。我不清楚。我们就要求他这样，或者可以给他一个约束力嘛，反正约束力又不做功。而且就算有别的什么力做功也算不到龙卷风头上）
我们还是先从没有龙卷风开始。没有龙卷风不代表没有力，就像没有进水口不代表没有水流一样。就说这个小物块受重力影响吧（牛顿引力场）可能还受电力影响（暂时忽略磁力，磁力比较复杂，但是其实从不做功）可能还受弹簧力影响。
我在重力场中，扔起一块石头，石头落在我手上。重力对石头并没有做功。在电场里仍起一个带电物体，又回来，仍不做功。实际上，这些场的共同点是：在其中运行的物体 -
7楼 - 8楼 2013-11-17 12:44 呜呱星人接上面）这些场的共同特点是：对一个在其中运动轨迹为封闭曲线的物体做得总功为零。这些场叫做保守场。
总功是宏观解释，我们再来看微观解释。stokes公式说的是曲面上场的法向分量面积分（眼熟么？对了和前面那个只差2点，那就是这里的曲面不是闭合的。那里的曲面是个椰子，这里的曲面是张床单。那里是积分场自身，这里是积分他的旋度）等于场在曲面边界上切向分量的线积分。
保守场的旋度为零（关于保守场我们可以说很多，不过都等价）于是乎面积分为零，线积分为零。
我们把龙卷风加回来，绕龙卷风一周，龙卷风做功不为零。微观解释是龙卷风风立场不是保守的，旋度不为零，于是乎积分不为零，总功不为零。
后面的讨论与上面大同小异了，有一点不一样的就是在第二种情况，边界和曲面再给出的时候是没有定向的，而定向的规则是约定俗成而确定的。所以说这一点不用担心床单反过来也能铺的问题。
No comments:
Post a Comment