最小作用量原理- 维基百科,自由的百科全书
zh.wikipedia.org/zh/最小作用量原理
转为简体网页
Chinese Wikipedia
Loading...
最小作用量原理_百度百科
baike.baidu.com/view/1988735.htm
Translate this page
Baidu Baike
Loading...
最小作用量原理与物理之美_百度文库
wenku.baidu.com/.../6c6adcd8d15abe23482f4def.htm...
Translate this page
[PDF]
光程. 作用量原理. 路径积分. 在电磁学领域, Fermat原理是一个重要的变分原 ... 必要从宏观的角度将最小作用量原理与Fermat 原理 ..... λ 为自由空间中频率为0f.
光程、Fermat原理与最小作用量原理之比较 - 中国科学:物理学 ...
phys.scichina.com:8083/.../downloadArticleFile.do?...
Translate this page
第三章、最小作用量原理 - 上海交通大学科学史与科学哲学系
shc2000.sjtu.edu.cn/.../...
Translate this page
Shanghai Jiao Tong University
Loading...
[PDF]
作为一个例子,考虑一个没有任何势能的自由粒子情况。我们知道粒子从 ..... 所以,
最小作用原理的一个例子:抛物体运动
staff.ustc.edu.cn/~phj/Classical_Mechanics/3_1.pdf
Translate this page
phymath999: 最小作用量原理与相位光程,折射率和光线实际 ...
phymath999.blogspot.com/2012/.../cnvsvtnsnvtct.htm...
Translate this page
音乐快递:phymath01 从拉格朗日函数到作用量,需要对时间 ...
《数理同源》-8-费曼的路径积分(一) - LaiLook知识网
www.lailook.net/klxx/03/2014-05-16/38260.html
Translate this page
《数理同源》-9-费曼的路径积分(二)  精选
精选

||
8. 费曼的路径积分(二)
不过,现在还有一个问题:上一节的推导过程是对时间间隔(t2-t1)趋于无限小的时候才能成立,如果对有限长的一段时间(t- t0)又该怎么办呢?费曼对此日思夜想,终于有一天(从梦中醒来后)感觉自己想通了:只需要将整个有限时间段分成很多很多个小时间段,对每一段都可以应用以上同样的做法。然后再令这些时间小段趋于零,而小段的数目趋于无穷大,加起来后求极限。最后,也同样能够在有限的时间区域中导出薛定谔方程【1】。
以经典拉格朗日量作为相位的传播子可以推导出薛定谔方程的这个事实,说明这种方法与薛定谔方程是等价的。所以现在,我们有了三种方法来描述量子力学:除了薛定谔的微分方程、海森堡的矩阵力学之外,又有了费曼的方法!这三种表述都能得到同样的波函数,然而,费曼这种方法到底是什么意思呢?如果按照费曼所想的办法,将有限的时间段分成无限多个小时间段,听起来倒也不是什么新花样,那不就是微积分的思想吗。不过,从上一节的叙述中可知,每一个时间小段的传播子,都包含了一个积分表达式。现在如果有无限多个小时间段的话,总的传播子就应该要做无限多次积分。那么,这无限多次积分的几何图像是什么呢?让我们从以上描述的费曼的思路过程来理解它。

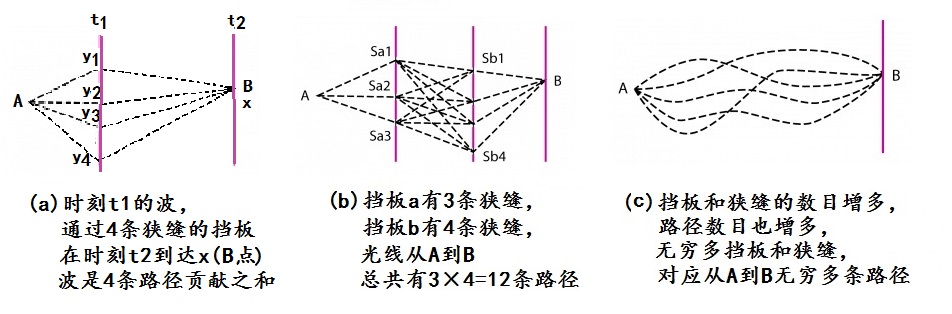
图2:从假想而设立的挡板来理解费曼路径积分
首先,我们考虑从A传播到B的粒子的几率波。如图2a所示,假设粒子传播的过程中,在t1时刻被一个有4条狭缝的挡板挡住了。如果(t2-t1)很小的话,那么,近似而言,这个粒子在t2时刻到达B点的几率是狭缝到B的4条直线路径的贡献之和。如果狭缝数增多,直线路径便增多,各条直线路径对几率的贡献也就相应地叠加上去。关键之点是:狭缝增加到无限多,实际上意味着没有了挡板!因而,没有挡板的情形下,t2时刻到达B点的几率是从t1时刻无限多个不同的位置连到B点的无限多条直线路径的贡献之和。现在,假设A和B之间的时间间隔不是“很小”,那么,的确和微积分的思想一样,现代数学的高招就是将这一段“有限”的时间间隔分成许多许多小间隔,然后对每一个小时间段都运用刚才的方法做一遍。比如说,我们考虑图2b有两个挡板的情形。第一个挡板有3条狭缝,第二个挡板有4条狭缝,那么这时候,这个粒子从A到B的几率是3*4=12条折线路径之和。换个说法,也就是两次求和之乘积。然后,沿用刚才的办法过渡到除去挡板的情形,也就是说,没有挡板的情形下,粒子从A到B的几率是中间两个时刻点无限多个不同的位置连到B点的无限多条“折线”路径的贡献之总和,或称之为二重积分。
再将上面的思路过程推广到A和B之间有n个时间点,即有n个挡板的情形。想象对每个挡板都将以上过程做一遍,然后便不难得出如下结论:粒子从A到B的几率是中间n个时刻点对应的无限多个不同的位置分别连到B点的无限多条“折线”路径的贡献之总和。或者说,是n次无限求和(即积分)之乘积。
再进一步,将时间间隔划分成无限多个时间点,如图2c所示,即令n趋于无穷。这时候,粒子从A到B的几率应该是无限多个积分之乘积。而上述解释过程中所谓的“折线”,也都变成了连续曲线,换言之,这无限多条曲线实际上就是代表了从A到B的所有任意形状的“路径”。
因此,可以将刚才的解释表达得更容易理解一些:从A到B的传播子,或转换函数,是从A到B的所有路径贡献之和。还可以引申成更为数学的语言:这儿的无限多重积分,可以看作是对所有路径的积分,换言之,对“路径空间”的积分。这个路径空间又是什么呢?是所有从A到B的三维曲线构成的空间,这就又回到了我们在本系列最开始介绍伯努利的变分法,即“最速降线问题”时候的那个泛函空间。如此一来,貌似高深的量子力学路径积分与那个简单的几何问题又联系起来了。
后来,费曼企图将这个作法应用到狄拉克的相对论性量子理论时,碰到了困难。再后来,费曼参加到原子弹研究的曼哈顿计划中,无暇顾及这个理论问题。不过他在1942年以此思想为基础完成了他的博士论文“量子力学中的最小作用原理”。大战之后,费曼受聘于康乃尔大学,继续他对量子理论问题的探讨。几年之后,费曼在他的博士论文的基础之上,完善了作用量量子化的路径积分方法。他1948年在《现代物理评论》上发表的“非相对论量子力学的空一时描
写”便是其划时代的代表作。几乎同时,费曼也成功地解决了量子电动力学中的重整化问题,创造出了著名的费曼图和费曼规则,用以方便快捷地近似计算粒子和光子相互作用问题。之后在60年代,费曼又发展了量子场论中的泛函积分方法,其实就是将单粒子的三维函数路径空间推广到场论的多维(无限维)路径空间而已,不过此是后话不表【2】。
费曼的路径积分是“最小作用量原理”在量子力学中的推广。它让我们完全从另外一个角度来理解爱因斯坦的问题:大自然是如何创造这个世界的?科学家们只能从自身的经验和人脑的思维想象来“揣摩”大自然的所谓“意图”。这里涉及到诸多的物理量之中,“哪些是最基本的?”这一类问题。比如说,物理学家最早发现了“力”的概念,后来又有了“能量”的概念。如果有孩子问你:“苹果为什么会掉下来,正好打到牛顿的头上呢?”你起码可以有两种方式回答这个问题。一种方式是从力的观点。你说:“苹果受到地球重力的吸引而下落,我们周围的空间中重力场无处不在,它作用到苹果上,使得苹果在每一个时空点都因为它受到的力而作相应的运动!”。另一种方式呢,你可以从能量的观点来回答:“苹果只有处于势能最低的位置才稳定。所以嘛,它就往下掉,往下掉,一直掉到势能最低无法再低的位置为止!”用更数学的观点来看待这两种说法,第一种是与力场的微分方程有关;第二种方法则是将“能量”视为更为基本的物理量;从前面几节中我们了解了最小作用量原理,所以,你还可以用“作用量”替代“能量”,用第三种说法来解释。也许用作用量来解释苹果的下落不是很直观,那么,我们在上一节中所举的光线、救援者、蚂蚁的行为,便为你提供了很好的实例。
回到理论物理。三个物理量中,力、能量、作用量,到底哪一个更为基本呢?当费曼刚开始提出量子力学的路径积分表述方法时,并未得到主流物理学家的赞同。波尔就是对此长期持反对态度的人之一。波尔实际上非常看重费曼的才华和直率的性格,费曼自己曾经讲过一个故事:按照费曼的说法,费曼刚加入曼哈顿计划时的波尔就如同物理界的神一般受到大家的尊敬。当时,尼尔·波耳任曼哈顿计划的顾问,和他的儿子一起多次到美国洛斯阿拉莫斯实验室访问。费曼如此生动地描述过波尔到来时的两次物理聚会【3】:
“第一次聚会时,我坐在后面的某个角落,只能在众多脑袋瓜的缝隙间看到一点点波耳的影子。但他第二次来开会的那天早上,我接到一个电话。是波尔的儿子打来的,说他父亲想和我谈谈。于是,我和波尔在一个办公室里反复讨论和争论了很久有关原子弹的很多想法。后来我才从小波尔那儿知道了事情的来由:原来上次他们来访后,老波耳跟他儿子说:‘记得坐在后面那小伙子的名字吗?他是这儿唯一一个不怕我的人,只有他会指出我的想法的荒谬。’因此,老波尔决定,下次要讨论什么问题时,不能只找那些只会说‘是,波耳博士!’的人谈话,于是,才在会议之前,先找了我这个‘小人物’去讨论了半天……”
但玻尔对费曼路径积分方法有所误解,还曾经把费曼图误解成粒子运动的轨迹,并对之进行了严厉的批评。没有明确的记载说明爱因斯坦是如何看待路径积分的。费曼和爱因斯坦接触很少,只有过3次短暂的见面。第一次是在普林斯顿大学物理系,1940年末,惠勒建议费曼在魏格纳教授负责的讨论会上报告他们的工作,魏格纳认为惠勒和费曼的工作很重要,他邀请了好几个重量级的大师:天文系的亨利·诺里斯教授、数学系的冯·诺伊曼、当时从苏黎世来访的泡利,当然还特别邀请了大名鼎鼎的爱因斯坦。当时,挑剔的泡利坐在爱因斯坦旁边,自己表示不认可惠勒和费曼的作法,并且询问爱因斯坦的看法,爱因斯坦含糊而温和地答了一句“no”。不过,那时候费曼有关路径积分的思想尚未成熟,报告中讲的主要是有关辐射阻尼的问题。后来,大约是1948年,惠勒曾经将费曼量子力学路径积分的论文交给爱因斯坦看,并对爱因斯坦说:“这个工作不错,对吧?”又问爱因斯坦:“现在,你该相信量子论的正确性了吧!”爱因斯坦也并未直接对费曼文章发表看法,而是沉思了好一会儿,脸色有些灰暗,怏怏不快地说:“也许我有些什么地方弄错了。不过,我仍旧不相信老头子(上帝)会掷骰子!”
六十年代之后,费曼通过他自身人格的魅力、风趣迷人的讲演风格、以及深入浅出的物理论著,使得路径积分的观点对年轻一代物理学家产生了巨大的影响,也逐渐得到老一代前辈的认可。
到七十年代,海森堡和狄拉克都转而相信,量子力学的基本特征是用以解释路径积分的带相位的几率幅,而不是非对易关系。
费曼则在《量子力学与路径积分》这本著作中说:“量子力学中的几率概念并没有改变”、
“所改变了的,并且根本地改变了的,是计算几率的方法。”因此,费曼对量子力学的观点,是基本属于统计诠释一派,只不过,他不是用解微分方程的方法,而是用路径积分的方法来计算几率而已。
微分方程是局域的、立足于力的概念,积分的方法是整体的、基于能量或作用量。这是看问题的两个不同角度,从力的角度看,能量为次级属性。如果从能量或作用量的角度看,力就是一个次级属性。费曼的路径积分使我们从另一个角度来理解量子力学。还不仅仅如此,有时候,更为基本的物理量的正确选择是具有物理意义的,比如AB(阿哈罗诺夫-波姆)效应便是一例。在此我们不再重复叙述,有兴趣者请参考笔者的另一篇博文【4】。

图3:经典到量子
根据路径积分法,从一个时空点(A,tA)到另一个时空点(B, tB)的几率幅,来自于所有可能路径的贡献,每一条路径的贡献的幅度一样,只有相位不同,而其相位则与经典作用量有关,等于(S/ℏ)。
在这儿ℏ是普朗克常数。因此,ℏ正好具有作用量的量纲,可以把它看作是作用量的量子,而S/ℏ表明了对应于每条路径的作用量S的量子化。换言之,路径的作用量子的数目决定了该路径对几率幅的贡献。
更为奇妙的是,路径积分在经典物理和量子物理之间架起了一座桥樑。对宏观尺度来说,作用量子ℏ是个很小很小的量,因此,对每条路线,S 都比ℏ大很多,对该路线的临近路径而言,相位的变化非常巨大而使得这些路径贡献的几率幅相互叠加互相抵消。但有一条路径附近的几率幅不会完全抵消。那就是当这条路径与其临近路线的相位变化不大基本上相同的那条路径,换句话说,也就是对相位的变分为0的那条路径,或者说是作用量S的变分为0的路径。说到这儿,我们已经知道了,那就是经典粒子的路径!如此而来,宏观而言,量子现象就过渡到了经典的运动轨迹,这也就是最小作用量原理与量子力学路径积分之间更深一层的关系。
参考资料:
No comments:
Post a Comment