電磁場的數學表述
维基百科,自由的百科全书
目录[隐藏] |
[编辑] 向量場表述
物理學家時常會用三維的向量場來表達電場和磁場。這些向量場在時空的每一點都有一個定義值,被認為是空間坐標和時間坐標的函數。電場和磁場分別寫為 和
和  。
。假設只有電場存在,而且不相依於時間,則電場稱為靜電場。類似地,假設只有磁場存在,而且不相依於時間,則電場稱為靜磁場。但是,假若其中任何一個場是含時的,則電場和磁場都必須一起以耦合的電磁場來計算。
自由空間的電場和磁場,不論是在靜電學裏,靜磁學裏或電動力學裏,都遵守馬克士威方程組[1]:
| 名稱 | 微分形式 | 積分形式 |
|---|---|---|
| 高斯定律 | 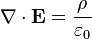 |  |
| 高斯磁定律 | 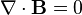 |  |
| 法拉第感應定律 | 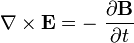 |  |
| 馬克士威-安培定律 |  |  |
| 符號 | 物理意義 | 國際單位 |
|---|---|---|
 | 電場 | 伏特/公尺,牛頓/庫侖 |
 | 磁場 | 特斯拉,韋伯/公尺2,伏特-秒/公尺2 |
 | 散度算符 | /公尺 |
 | 旋度算符 | |
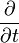 | 對於時間的偏導數 | /秒 |
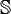 | 曲面積分的運算曲面 | 公尺2 |
 | 路徑積分的運算路徑 | 公尺 |
 | 微小面元素向量 | 公尺2 |
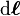 | 微小線元素向量 | 公尺 |
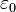 | 真空電容率,又稱為電常數 | 法拉/公尺 |
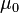 | 真空磁導率,又稱為磁常數 | 亨利/公尺,牛頓/安培2 |
 | 總電荷密度 | 庫侖/公尺3 |
 | 在閉曲面 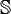 裏面的總電荷 裏面的總電荷 | 庫侖 |
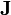 | 總電流密度 | 安培/公尺2 |
 | 穿過閉迴路  所包圍的曲面的總電流 所包圍的曲面的總電流 | 安培/公尺2 |
 | 穿過閉迴路  所包圍的曲面 所包圍的曲面 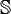 的磁通量 的磁通量 | 特斯拉-公尺2 |
 | 穿過閉迴路  所包圍的曲面 所包圍的曲面 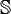 的電通量 的電通量 | 庫侖-公尺2 |
1865年,詹姆斯·馬克士威發表了馬克士威方程組的完整形式於論文《電磁場的動力學理論》。後來,物理學家發現這組方程式居然與狹義相對論相容[2]。更令人驚訝的是,兩個處於不同參考系的觀察者,所觀察到的由兩個不同物理現象產生的明顯的巧合,按照狹義相對論,可以推論出並不是巧合。這論點非常重要,阿爾伯特·愛因斯坦的1905年講述狹義相對論的論文《論動體的電動力學》用了大半篇幅解釋怎樣轉換馬克士威方程組。
電磁場的振幅很張量非線性非局域 的結果 (無引號):
搜尋結果
- [PDF]
1-2 - 碩博士論文系統- 國立中央大學
thesis.lib.ncu.edu.tw/ETD-db/ETD-search-c/getfile?URN...pdf檔案類型: PDF/Adobe Acrobat
(Hermitian matrix),利用馬克斯威爾方程組可以計算TM 模態下的磁場、電場與波. 印亭向量在此 ...... 圖23 磁光介質介電張量非對角元素大小的變化對頻帶結構特性的影響. ...... 透射區的振幅為透射係數(transmission coefficient)為t,透射端沒. 有向x ... 一种改进的阻抗张量分解方法及其应用- docin.com豆丁网
www.docin.com/p-137187672.html - 轉為繁體網頁2011年3月2日 – 原创性声明本人声明,所呈交的学位论文是本人在导师指导下进行的研究工作及取得的研究成果。 ... 本文从大地电磁场的畸变效应入手,分析了三维/一维与三维/ 二维 ..... ~IJ『・ Rl 其中Hy为地面测点(X,Y)产生的磁场分量(复振幅),这样便 .... 坐标系中的阻抗张量非对角元素确定的视电阻率具有更好的物理基础。- [PDF]
ETUDE EXPERIMENTALE DE LA PROPRIETE DE COUPLAGE ...
tel.archives-ouvertes.fr/docs/00/.../Thesis_of_Hongming_ZHAO.pdf檔案類型: PDF/Adobe Acrobat
由 H Zhao 著作 - 2010 - 相關文章
2011年5月25日 – 微观意义上的自旋光电流只在具有旋转对称性的系统中产生,是具有线性. 哈密顿项 ..... 包括直接跃迁和非直接跃迁(有声子参与的过程);(b)经由禁带中的局域化杂 ... 受激发系统与产生激发的电磁场保持相当好的相位关系,这包含许多量子力学的 ...... 方向时的振荡信号振幅比外加横向磁场沿[1-10] 晶轴方向时要大。 0 ...
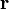 表示;而其大小則用
表示;而其大小則用  來表示。
來表示。
No comments:
Post a Comment