勒贝格测度- 维基百科,自由的百科全书
zh.wikipedia.org/zh-hk/勒贝格测度
轉為繁體網頁
轉為繁體網頁
概率空間- 维基百科,自由的百科全书
zh.wikipedia.org/zh-hk/概率空間
第二章勒贝格测度_百度文库
wenku.baidu.com/view/27e0cad73186bceb19e8bb23.html
轉為繁體網頁
轉為繁體網頁
有理数的测度_百度文库
wenku.baidu.com/view/b9d61eceda38376baf1faebc.html
轉為繁體網頁
轉為繁體網頁
几何测度论(二)---测度论基础(下) - 数学伊甸园- 博客园
www.cnblogs.com/suyh/p/3498356.html
轉為繁體網頁
轉為繁體網頁
熵(Entropy) (第2 頁)
episte.math.ntu.edu.tw/articles/mm/mm_13_3_01/page2.html
概率空間[编辑]
维基百科,自由的百科全书
概率空間是概率論的基礎。概率的嚴格定義基于這個概念。
第一項Ω是一個非空集合,有時稱作“樣本空間”。Ω 的集合元素稱作“樣本輸出”,可寫作ω。
第二項F是樣本空間Ω的幂集的一個非空子集。F的集合元素稱為事件Σ。事件Σ是樣本空間Ω的子集。集合F必須是一個σ-代數:
第三項P稱為概率,或者概率測度。這是一個從集合F到實數域R的函數, 。每個事件都被此函數賦予一個0和1之間的概率值。
。每個事件都被此函數賦予一個0和1之間的概率值。
概率測度經常以黑体表示,例如 或
或 ,也可用符號"Pr"來表示。
,也可用符號"Pr"來表示。
為簡便起見,{ω∈Ω:X(ω)>0}經常只寫作{X>0}。P({X>0})更被簡化為P(X>0)。
若任何与隨机變量X有關的事件和任何与隨机變量Y有關的事件獨立,則X和Y兩個隨机變量是獨立的。
獨立這個概念是概率論和測度論分道扬镳的地方。
若兩個事件A和B不相交,則P(A∪B)=P(A)+P(B)。這個性質可以擴展到由(有限個或者可數無限個)事件組成的事件序列。 但不可數無限個事件組成的事件集合對應的概率与集合元素對應概率之和未必相等,例如若Z是正態分佈的隨机變量,則對任意x有P(Z=x)=0,但是P(Z是實數)=1。
事件A∩B的意思是A并且B;事件A∪B的意思是A或者B.
勒贝格测度[编辑]
定義[编辑]
概率空間(Ω, F, P)是一個總測度為1的測度空間(即P(Ω)=1).第一項Ω是一個非空集合,有時稱作“樣本空間”。Ω 的集合元素稱作“樣本輸出”,可寫作ω。
第二項F是樣本空間Ω的幂集的一個非空子集。F的集合元素稱為事件Σ。事件Σ是樣本空間Ω的子集。集合F必須是一個σ-代數:
 ;
;- 若
 ,則
,則 ;
; - 若
 ,
,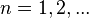 ,則
,則
第三項P稱為概率,或者概率測度。這是一個從集合F到實數域R的函數,
 。每個事件都被此函數賦予一個0和1之間的概率值。
。每個事件都被此函數賦予一個0和1之間的概率值。概率測度經常以黑体表示,例如
 或
或 ,也可用符號"Pr"來表示。
,也可用符號"Pr"來表示。例子[编辑]
若樣本空間是關于一個机會均等的拋硬幣動作,則樣本輸出為“正面”或“反面”。事件為:- {正面},其概率為0.5。
- {反面},其概率為0.5。
- { }=∅ 非正非反,其概率為0.
- {正面,反面},不是正面就是反面,這是Ω,其概率為1。
相關概念[编辑]
隨机變量[编辑]
隨机變量是一個從Ω映射到另一個集合(通常是實數域R)的函數。 它必須是一個可测函數。比如說,若X是一個實隨机變量,則使X為正的樣本輸出的集合{ω∈Ω:X(ω)>0}是一個事件。為簡便起見,{ω∈Ω:X(ω)>0}經常只寫作{X>0}。P({X>0})更被簡化為P(X>0)。
獨立[编辑]
若P(A∩B)=P(A)P(B),則A和B兩個事件是独立的。若任何与隨机變量X有關的事件和任何与隨机變量Y有關的事件獨立,則X和Y兩個隨机變量是獨立的。
獨立這個概念是概率論和測度論分道扬镳的地方。
互斥[编辑]
若P(A∩B)=0,则稱A和B兩個事件互斥或不相交(這個性質要比A∩B=∅弱一些,后者是集合不相交的定義)。若兩個事件A和B不相交,則P(A∪B)=P(A)+P(B)。這個性質可以擴展到由(有限個或者可數無限個)事件組成的事件序列。 但不可數無限個事件組成的事件集合對應的概率与集合元素對應概率之和未必相等,例如若Z是正態分佈的隨机變量,則對任意x有P(Z=x)=0,但是P(Z是實數)=1。
事件A∩B的意思是A并且B;事件A∪B的意思是A或者B.
勒贝格测度[编辑]
维基百科,自由的百科全书
数学上,勒贝格测度是赋予欧几里得空间的子集一个长度、面积、或者体积的标准方法。它广泛应用于实分析,特别是用于定义勒贝格积分。可以赋予一个体积的集合被称为勒贝格可测;勒贝格可测集A的体积或者说测度记作λ(A)。一个值为∞的勒贝格测度是可能的,但是即使如此,在假设选择公理成立时,Rn的所有子集也不都是勒贝格可测的。不可测集的“奇特”行为导致了巴拿赫-塔斯基悖论这样的命题,它是选择公理的一个结果。
我们想构造一个映射m,它能将实数集的子集E映射为非负实数mE。称这样的映射(集函数)为集合E的测度。最理想的情况应该是m具有以下性质:
目录
[隐藏]问题起源[编辑]
人们知道,区间的长度可以定义为端点值之差。若干个不交区间的并的长度应当是它们的长度之和。于是人们希望将长度的概念推广为比区间更复杂的集合。我们想构造一个映射m,它能将实数集的子集E映射为非负实数mE。称这样的映射(集函数)为集合E的测度。最理想的情况应该是m具有以下性质:
- mE对于实数集的所有子集E都有定义。
- 对于一个区间I,mI应当等于其长度(端点数值之差)。
- 如果{En}是一列不相交的集合,并且m在其上有定义,那么
 。
。 - m具有平移不变性,即如果一个m有定义的集合E的每个元素都加一个相同的实数(定义为
 ,记作E+y),那么m(E+y)=mE。
,记作E+y),那么m(E+y)=mE。
No comments:
Post a Comment