维基百科,自由的百科全书
本條目存在如下問題,請協助改善本條目或在討論頁針對議題發表看法。
|
| 当前條目的内容正在依照en:Third_law_of_thermodynamics的内容进行翻译。(2014年1月27日) 如果您熟知条目内容并擅长翻译,欢迎协助改善或校对这篇條目,长期闲置的非中文内容可能会被移除。目前的翻译进度为:
|
| 热力学 |
|---|

经典的卡诺热机
|
这一定律由瓦尔特·能斯特归纳得出,并提出其表述,因而又常被称为能斯特定理或能斯特假定。1923年,吉爾伯特·牛頓·路易士和梅尔·兰德尔提出另一种表述。
随着统计力学的发展,这一定律,正如其他热力学定律一样,得到了解释,而不再是只能由实验验证的经验定律。
这一定律虽然由于适用条件的限制,应用范围并不如热力学第一、第二定律广泛,但仍有重要意义——特别是在物理化学领域。[1]
目录
[隐藏]定律的引出和表述[编辑]
定律的解释[编辑]
定律的数学表述[编辑]
考察一个内部处于热力学平衡的封闭系统。由于系统处于平衡态,其内部不会进行不可逆过程,因而熵增为零。定律的实验验证[编辑]
由定律可得到的几个结论[编辑]
绝对零度是不可达到的[编辑]
File:Can T=0 be reached.jpg
当温度趋近绝对零度时,只有熵不是常值时,才能通过有限的过程达到,否则是不可能的
熱容量[编辑]
蒸汽压[编辑]
潜热[编辑]
³He和⁴He的熔化曲线在有限压强下都会延伸趋近绝对零度。在熔化曲线上各点表述的条件下,系统会处于固液相平衡。而热力学第三定律要求在温度为绝对零度时(如果能达到),系统的熵(无论物质处于何种物态)为定值。由此,可以推出在绝对零度时(如果能达到),系统熔化的潜热是零。另外,在这一结论基础上,通过克劳修斯-克拉佩龙方程可以得到,熔化曲线在绝对零度点的切线斜率为零。热膨胀系数[编辑]
热膨胀系数定义为 。
。考虑麦克斯韦关系,

和式(8) 取 X为p时的情况,
可以看出
 ,即对于任何材料,当温度趋于绝对零度时,其热膨胀系数也会趋于零。
,即对于任何材料,当温度趋于绝对零度时,其热膨胀系数也会趋于零。第5讲.ppt
cc.sjtu.edu.cn/G2S/Utility/download2.aspx?type=2...
轉為繁體網頁
[PPT]
(3)归纳法推理要以自然齐一律和普遍因果定律为基础,但二者没有经验的证据,只不过 ..... 拉梅—1814年入学,弹性力学创始人; 卡诺—1812年入学,热力学第二定律
第7讲工业革命与启蒙运动 - 课程中心
cc.sjtu.edu.cn/G2S/Utility/download2.aspx?type=2...
轉為繁體網頁
[DOC]
从可行性、加快速率、提高效率和效益的角度,应用热力学和动力学原理解决 ... 的标准平衡常数分别为K1θ,K2θ,K3θ,从盖斯定律及Kθ与△Gθ的关系出发,讨论各 ...
大学化学思考题.doc
cc.sjtu.edu.cn/G2S/Utility/download2.aspx?type=2...
轉為繁體網頁
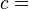








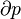
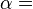

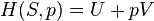

No comments:
Post a Comment