维基百科,自由的百科全书
 ;
;
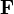 是連心力,
是連心力,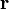 是從力中心點到檢驗位置的徑向向量。
是從力中心點到檢驗位置的徑向向量。連心力可以進一步細分為兩種版本:強版本和弱版本。強版連心力要求連心力相依於徑向距離:
 。
。
目录[隐藏] |
[编辑] 角動量恆定
假設一個粒子,感受到連心力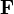 的作用,則施加於此粒子的力矩
的作用,則施加於此粒子的力矩 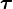 為零:
為零: 。
。
 對於時間
對於時間 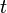 的導數是力矩:
的導數是力矩: 。
。
[编辑] 平面運動
關於此粒子的運動, 。
。
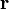 垂直於恆定的角動量
垂直於恆定的角動量  ,所以,此粒子的運動必局限於垂直於角動量的平面。
,所以,此粒子的運動必局限於垂直於角動量的平面。[编辑] 平面速度恆定
採用極坐標系 來表示此粒子的平面運動,原點為力中心點。則角動量為
來表示此粒子的平面運動,原點為力中心點。則角動量為 ;
;
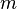 是粒子的質量、
是粒子的質量、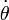 是角速度。
是角速度。粒子與力中心點的連線,掃過的平面的平面速度
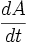 為
為 。
。
[编辑] 連心勢
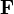 是一個函數
是一個函數  的負梯度:
的負梯度: ,
,
- 連心力的旋度是 0 :
 ,
,
- 對於任何簡單的閉合迴路,連心力所做的機械功
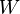 是 0 :
是 0 :
 。
。
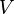 是一個純量勢,注意到由於
是一個純量勢,注意到由於  ,純量勢
,純量勢 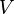 只能相依於
只能相依於  :
: 。
。
 為連心勢。連心力也只能相依於
為連心勢。連心力也只能相依於  :
: 。
。
[编辑] 有效勢能
一个運動於勢能 的粒子的拉格朗日量等於動能减去勢能:
的粒子的拉格朗日量等於動能减去勢能: 。
。
 、
、 ;
;
 為連心力。
為連心力。由於連心勢與角坐標
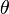 無關,因此其共軛動量(角動量)是個運動常數:
無關,因此其共軛動量(角動量)是個運動常數: 。
。
![\dot{p}_{r} = - \frac{\mathrm{d}}{\mathrm{d}r} \left[ \frac{P_{\theta}^2}{2 m r^2} + V(r) \right]\,\!](http://upload.wikimedia.org/math/2/0/8/208a80650c90ed2cfcc32829f0a28da5.png) 。
。
 。
。
 萬有引力下運動的有效勢能是:
萬有引力下運動的有效勢能是: 。
。
[编辑] 有心运动的轨迹的确定
有心力的运动轨道可以用比内(Binet)公式来计算。在平面极坐标系中,如果令: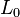 为物体做有心运动时的角动量,则有:
为物体做有心运动时的角动量,则有:[编辑] 平方反比类有心力的运动轨迹方程
将大小与到力心位置距离成平方反比的有心力表示为: ,将它代入上述的方程,得到:
,将它代入上述的方程,得到: 为移项整理后关于
为移项整理后关于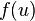 这个多项式的外层系数。通过类比弹簧振子简谐运动方程的求解方法[4],可以类似地解得上述方程的通解:
这个多项式的外层系数。通过类比弹簧振子简谐运动方程的求解方法[4],可以类似地解得上述方程的通解:





No comments:
Post a Comment