引子:
CDMA是个很重要的通信概念,很多的大学教科书上都会提到它,甚至我们今天可能都在使用它。然而提到cdma,很少有资料提到它的思想是多么的有创意,教科书上关于cdma的章节都过于复杂,过于数学化,虽然也有一些简便的描述方式,但是却几乎没有资料揭示cdma是多么的简单,实际上它比其他很多的概念都要更简单。
如果仅仅希望理解诸如cdma的概念而不得不去学习一大堆数学是很悲哀的事情!如果最终你费了九牛二虎之力把数学推理过程搞明白了,你对数学本身的理解将超过你对cdma的理解,本来数学仅仅是为了帮忙理解cdma,可是最终却反客为主了。我认为理解一个概念最好不要从数学开始,数学化的东西只是一个总结,一种表述方式罢了,正如音乐的实质不在五线谱原理和简谱助记法而在旋律本身一样,我敢肯定任何科学理论的提出都不是从数学开始的,但是却总是归于数学,正如任何伟大的音乐作品只从音乐本身开始,伟大的美术作品的作者不需要事先研究配色原理一样。记住,数学只是工具!
一.开始吧,从吉普赛纸牌开始
小的时候,我们都玩过吉普赛纸牌,用来算自己某天会不会有“桃花运”,这种纸牌算出来的桃花运像魔咒一样,使腼腆的你对你喜欢的小女孩说“我喜欢你”(我就这么玩过,结果很尴尬...),不知道为什么这种游戏现在没有人玩了。表面上每张牌上写满了乱七八糟的文字,如下图:

然而当你用一张挖有小洞的纸牌罩在写满字的纸牌上的时候,你会发现上面写着一句话,如下所示:

这种游戏也许和我们现在玩的《愤怒的小鸟》之类的相比有点傻,然而它确实是一个古老的游戏,本文的目的不是为了揭示游戏原理,而是它有助于我们理解cdma。
我们把写满文件的纸牌看做是“仅有一个有效信号,其它对于接收者来讲全是噪音”的叠加信号,而挖有小洞的纸牌就是分配给每一个人的“码”,每一个“码”都不同,因此当用这些码罩到叠加信号上时,能显示出的只是我们感兴趣的信息,比如“你有桃花运”。就这么简单,所有的信号尽管发过来好了,我不怕干扰,因为我用我的“码”可以解出发给我的信息。
显然,如果一张牌上能写100个字,每句有意义的话有5个字,那么我们就可以设计出20张挖有小洞的纸牌作为“码”,每张纸牌上有5个洞,能通透5个字。如果没有“码”,100个字看起来就是乱码,因此这种方式还起到了一定的信息加密的作用。20个码分给20个人,就可以通信了,在和对方交换信息前,先用对方的码把信息填到相应的位置,对方收到后就自己的码往纸牌上一罩,结果就出来。
所谓的码分多址最终就归于一副吉普赛纸牌上。很简单吧
二.好吧,再看看别的例子
除了吉普赛纸牌,其实我们每天都在接触码分多址:
1.大学刚开学的时候,军训时,在火车上,飞机上,大家聊天时,你能一耳朵听出谁是你的老乡,因为有时候别人使用的方言你根本听不懂,也就是说你没有理解那种语言的“码”,我们的大脑中天生拥有一种过滤母语或者方言的“码”!
2.长途旅行中,你很困,旁边的两个家伙叽叽喳喳说个不停,如果他们使用你听不懂的语言,你照样能睡着,但是如果他们说的是普通话,那你就完蛋了,那就忍耐吧
三.该我们自己设计了
大自然已经设计了我们的大脑这种高度复杂的“码分多址设备”,我们当然使用这个设备也能造出一个克隆体,如果我们就是上帝,那么我们希望造出和我们一样的东西,因此码分多址技术是必然要出现的,如果你不承认它是一种创意,起码它也是我们自身的印照!
通过吉普赛纸牌,我们发现,码分多址的要点在于诸多的“码”本身是不能互相干扰的“掩码”,它有两个特点:
一是码之间两两不能互相干扰(因为不能在纸牌的一个位置写下两个不同的字);
二就是它们是掩码,所谓的掩码就是将不需要的信息“掩去”。
这就是要点,我们只要能设计出类似的编码规则就可以了,这难道很难吗?
理解了上述的“码”的两个基本特征之后,接下来再考虑数学实现也不迟,我当然还是试图不使用数学,期望在全文中不提什么“沃尔什函数”,“正交”,“卷积”之类的概念,可是我觉得还是有必要阐述一下,因为第一,正交的概念真是太美了,一下子就把上述两个特征都实现了;第二,不使用那些复杂的推导过程也能理解上述的数学概念,没有学过微积分和矩阵原理也没有问题。
四.为什么需要数学
任何领域几乎都需要数学,数学确实是一个好东西,它不仅仅是一种工具,它还是一种大脑训练操。因为它足够抽象,能够很方便的建模,使各领域的设计师将精力集中在该领域本身,纯逻辑和纯理论抽象的部分交给数学来解决,由于现代数学是建立在一整套很严密的逻辑的基础上的,因此它的结论一般不容置疑(当然不要考虑哥德尔考虑的问题,那是数学家和逻辑学家的工作),而且在数学推理过程中,可以排除特定领域的概念干扰,比如在基于牛顿第二定律计算运动物体速度时,可以排除接触面粗糙程序,阻尼等物理概念。数学完全符合高内聚低耦合的特征,因此虽然数学看起来很令人讨厌,然而当你熟悉了它之后,它真的很有趣!能使我一心一意工作的诱惑有两个,一个是加薪,另一个就是数学,真的是这样(虽然平时不怎么使用数学,然而数学带来的不是知识本身,不是会背几个公式知道几个名词,值得享受的是思考的过程和从中总结出的“道”)。
然而切记,只有两种情况下使用数学,一种是你在体验数学本身,二是你使用它描述或者解决问题,并且此时你已经彻底理解了问题的本质。(有些顶级草根黑客认为代码需要想到及写出,然后慢慢修改调试,正如画油画一样,而大部分公司的经理却厌恶这种论调,他们总希望你在编码之前先提交一堆文档,然后等到最后再用最短的时间编码,这也许就是艺术和技术的区别吧?)
五.先从最简单的情况看起
如果问一个初中生,力是如何合成的,如何分解的,他会马上说出矢量,正交,坐标系,cos,sin等概念,既然初中生都明白力是怎么合成的,那么咱们作为一群大学都毕了业好几年的家伙,怎能不知呢?你如果否定,那既然你知道力是如何合成和分解的,怎么就不能理解码分多址呢?
考虑最简单的只有两个码的码分多址中,叠加的信号就是一个两个个力的合力矢量,而特定用户解出的属于自己的信息就是该合力在一个坐标轴上的分力,他们使用的“码”就是坐标轴上的单位矢量,且坐标轴是正交的(相互垂直的笛卡尔坐标系)。如下图:
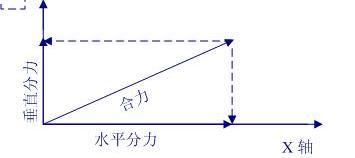
很简单吧,实际上也真是这么简单。回忆吉普赛纸牌,是不是很一致呢,我们可以设纸牌上可以写20个字,一个作为码的纸牌上可以挖10个洞,只要两张挖洞纸牌上的洞的位置不重合,那么可以认为这两张挖洞纸牌就是正交的。第二个特征是掩码,实际上可以通过正交推理出来,因为正交概念本身就是井水不犯河水的关系,顺着笛卡尔坐标系的x轴向原点望去,你只能看到y轴,而看不到x轴,反过来沿着y轴向原点看,你也只能看到x轴,是不是掩码的意思呢?一个正交的概念解决了两个问题。如下图:

以合力解释这个叠加信息的编码是很容易理解的,合力仅仅是实际力的合成,是实际力-垂直力和水平力的承载体,以力的效果来说明它们互相不干扰就是:水平力不会造成物理在垂直方向有位移,垂直力也不会造成物体在水平方向有位移,应用在信息上,用户A使用码X编码的信息i1和用户B使用码Y编码的信息i2最终叠加成了I,也就是合力,然而某一用户如果使用码X将信息I分解,它得到的将是i1,对i2丝毫没有影响,为什么呢?因为码X和码Y是正交的,正如上述的X轴和Y轴正交一样。
六.稍微扩展一点正交,没想到,就这样结束了
归纳能力是人类特有的能力,有趣的是,人们归纳曾经发生的过事的目的恰恰是为了预测未来的事。笛卡尔坐标系是欧几里得空间的正交系,它可以解决和解释大量的问题,然而直到17世纪,数学仍然没有作为一个独立的学科发挥巨大的作用,原因正是到那时为止,数学太形象化了,直到微积分和希尔伯特空间被提出来,数学才从具体的学科中被抽出来,专门向更抽象和逻辑性更强的方向发展。这种发展最终反过来影响着具体的学科,受其影响最大的学科就是物理学和信息学了。
如果大家理解了上述的枝枝蔓蔓,此时就可以一头扎进数学了,但是注意,千万不要恋战,点到为止,再次重申,数学只是工具,除非你想专门研究它!
既然二维的笛卡尔正交系可以抽出两个正交量从而形成两个所谓的“码”,那么如果有一个正交系有N个正交量,那么不就是说有N个“码”了吗?是的,确实正确!并且这样的正交系是存在的,数学作为工具在此发挥了作用。
要讲述正交的概念,很多教科书本着先导出概念的原则先讲述了向量,然后讲述了内积之类的概念,最终告诉你内积为0的两个向量是正交的,当你得到这个答案的时候,你可能已经被内积以及之前的概念搞糊涂了,或者已经厌烦了,已经忘记了当初为何需要知道什么是正交,以及需要正交的哪些性质,因此这种教育方式对于喜欢科学探索的家伙来讲无疑是毒药!什么是正交呢?简单点说两个正交量肯定是相交的,也就是有联系的,但是这种联系很“正”,也就是除了在交点发生关系之外,其它哪里都不发生关系,只要满足这两点都是正交的量,对于二维空间,直角坐标系的x轴和y轴在原点相交,它们又彼此垂直,彼此在对方没有任何分量,因此它们正交。对于超过3个的多个量,只要满足“相关联”,“关系很正”这两个性质都属于正交量,因此理解了这一步,我们看看数学语言是如何描述它的,对于连续量,使用积分来描述,对于离散量来讲,就更简单了,如果我们设空间有M个分量,那么一个向量将表示为:

这就是多维空间的正交向量,就这么简单。如果我们把这样的向量作为“码”分给每一个用户,那么用户用这个向量码和自己的标量信息做一个算术乘法,作为结果Rn,Rn显然也是一个多维向量,然后所有的用户的这些Rn加在一起:R1+R2+...Rm,最终形成一个M维空间的向量,这就相当于一个合力,信息到达接收端后,用户只需要将“合力”分解到自己的“码”上就可以了,注意,为了使运算简单,最好使用单位向量作为码。
六.构造多维正交向量
原理就是这么简单,可是我们怎么去构造这么一组向量满足式子(1)然后从而分配给用户呢?如果你独自思考问题到了这个地步,接下来你要干什么你自己就很明了了,如果你觉得你是个天才,你就去自己去想个办法,如果你觉得你只是想弄明白cdma的原理或者在搞一个新的编码或者别的,那么你肯定去阅读相关的数学资料了。看到了吗?我们第二次使用数学,前一次搞明白了希尔伯特空间向量,这次我们需要搞到一个简单的,且能得到多个正交的向量的方法,是什么呢?哎,最终还是要提到沃尔什函数,Ahha!
还是我的老原则,那就是先看效果,然后反思,或者说试图从一个巨人的脚后跟往上爬,最终爬到另一个巨人的肩膀!好了,先看一眼沃尔什向量长什么样子吧:
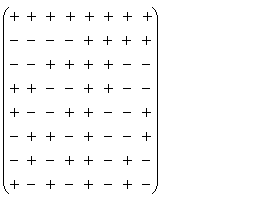
【和大多数教科书一样,我将“1”换成了“+”,将“-1”换成了“-”,沃尔什矩阵中只有“1”和“-1”】
不管怎样,先不管它的原理,看看任意两行或者任意两列,显然是正交的,完全符合需求,然后,和那个力的合成和分解一样,就算就可以了,超级简单,在理解原理前,我们先看看如何进行cdma的核心编码,当我们发现其简单性之后,再来考虑原理,最终我们会为这一切配合的如此完美而叹为观止!
七.沃尔什编码的简单性使得CDMA大有前途
沃尔什矩阵如何编码数据呢?我们知道数据都是0和1组成的,这就更好办了。首先为每一个用户分配一个N阶沃尔什矩阵中的一行或者一列(要么全是行要么全是列),将数据的0,1序列和向量相乘,这是纯粹是标量和向量的乘法,乘以分量即可,...(当然事实上没有这么简单,编码问题什么时候都是很复杂的,然而本文主要帮助大家理解cdma的本质,而不是研究如何编码)。我以一个实例结束核心讨论:
1.用户1的码:a1=(-1 -1 -1 -1 1 1 1 1)--第2行
2.用户2的码:a2=(-1 1 -1 1 1 -1 1 -1)--第7行
3.用户1的数据:d1=110
4.用户2的数据:d2=010
下面开始编码过程,假设发给用户1和用户2的数据叠加在一起,用户1的数据最终成为:
(-1 -1 -1 -1 1 1 1 1)|(-1 -1 -1 -1 1 1 1 1)|(0 0 0 0 0 0 0 0)【前面的|隔开的是用户1的三位数据编码后的结果,每一位用户数据都是标量,和码相乘,结果还是向量】;用户2的数据最终为:
(0 0 0 0 0 0 0 0)|(-1 1 -1 1 1 -1 1 -1)|(0 0 0 0 0 0 0 0),二者叠加后为:
(-1 -1 -1 -1 1 1 1 1)|(-1 -1 -1 -1 1 1 1 1)|(0 0 0 0 0 0 0 0)
(0 0 0 0 0 0 0 0)|(-1 1 -1 1 1 -1 1 -1)|(0 0 0 0 0 0 0 0)
_______________________________________________________________
(-1 -1 -1 -1 1 1 1 1)|(-2 0 -2 0 2 0 2 0)|(0 0 0 0 0 0 0 0)
最终结果是:
(-1 -1 -1 -1 1 1 1 1)|(-2 0 -2 0 2 0 2 0)|(0 0 0 0 0 0 0 0)
这个叠加的数据同时到达用户1和用户2,用户1解码的过程实际上是一个“力的分解”过程,如果是二维的情况,如果我们知道有一个“合力”是(a b),那么要求在x轴上的投影向量,我们该怎么办?其实我们不必求投影向量,只求投影的长度即可,毕竟被编码的数据是标量啊!这就更简单了,随便问一个初中生估计能得到最简单的答案。答案就是:L乘以夹角的余弦值!
然而对于多维向量而言,L是不易的,因为多维向量不好用【勾股定理】(我更喜欢用毕达哥拉斯定理这个词)。那么怎么办呢?向量的事最好由向量自己解决,记住,有很多我们中学时学习到的定理或者公式都是不适合高维空间的,毕竟那是古人经验(计算车轮子的长度,计算横梁)或者纯思辨哲学(苏格拉底,柏拉图,亚里士多德的时代)的成果,那时数学还没有抽象到希尔伯特时代的程度,因此我们还是用现代的方法吧!现代的方法为:

所以忘掉中学时的知识吧。如果我不进一步说明上述的公式是怎样导出的,我还是落入了俗套,因此,我给出简单的推导,哪怕是一点指点迷津的思路也行:

起初数据为k,然后和数据r一起被编码并且叠加在一起,最终又恢复了k,一切使用的都是矩阵的加法和乘法运算,最幸运的是,这些运算都是很简单的。
CDMA的本质理解了吗?实际上,这种方式如此简单的解决了码分多址编码问题,使用了这种方式之后,可以巧妙绕开那些相对复杂的变换或者逼近,比如傅里叶变换和离散余弦变换,因为再也不需要那种方式了,使用CDMA的方式可以使得频谱越宽越有效,而且再也不用靠增加功率来传输信号啦,扩频通信由来于此!
那么沃尔什矩阵究竟是怎么来的呢?可能是沃尔什本人靠他天才的大脑想出来的,也可能...最重要的是,如果理解了哈达玛矩阵的话,理解沃尔什矩阵就简单多了,因为哈达玛矩阵是沃尔什矩阵的一种表述方式,它的最重要的特征就是其递推性,从低阶的矩阵可以推导出高阶的,而且生成原则很简单,仅凭如此它就比其它的编码方式更具优势,更别说它的码分多址特性了。
八.凯撒加密和扩展的凯撒加密
在古代,如果手持一张羊皮纸,上面写着乱七八糟的文字,然后如果有一个人拿着一张打着窟窿眼的羊皮贴到写字的羊皮上之后,就能复原信息,窟窿眼在不同的位置,信息呈现就会有所不同,这是一种数据加密的方式,同时也是一种数据复用的方式,这叫什么呢?其实这就是码分多址啊!因此码分多址天生就和加密不可分,这种编码方式天生具有安全性,究其深层原因,实质在于“码”本身参与了编码,而码是特定区间内用户唯一的,这个码可以理解成密钥,也可以理解成收发方作为一个整体共享的私钥!
彻底理解了码分多址的本质之后,发现它的简单性以及优美原来来源于它靠向量本身编码,我们提到向量觉得起码得要二维才行,实际上我们更希望从1开始,想想看,一维数轴上的数字难道不是向量吗?如果我们使用一维的向量来进行编码,实际上就会发现这原来就是扩展的凯撒加密运算。
什么是凯撒加密呢?简单的说,凯撒加密需要一个10进制的数字k作为密钥,然后初始信息的每一个字母编码为其在字母表中位置加上k的位置处的字母。
扩展的凯撒加密就是使用一个序列a1,a2,a3,...aM作为密钥,然后将待加密的字母序列中每一个字母bN编码为字母表中其所在位置加上aN的位置处的字母,是不是和本文开始处的吉普赛纸牌很相似呢?没有挖洞的吉普赛纸牌我们看不懂写满文字的吉普赛纸牌中的信息含义,因此吉普赛纸牌天生就有保密性的特性,且它和凯撒加密法又是如此相似,并且,更简单的一个例子,如果一个吉普赛人在中国大骂,我们十有八九听不懂他们的话,依然会微笑!
CDMA是个很重要的通信概念,很多的大学教科书上都会提到它,甚至我们今天可能都在使用它。然而提到cdma,很少有资料提到它的思想是多么的有创意,教科书上关于cdma的章节都过于复杂,过于数学化,虽然也有一些简便的描述方式,但是却几乎没有资料揭示cdma是多么的简单,实际上它比其他很多的概念都要更简单。
如果仅仅希望理解诸如cdma的概念而不得不去学习一大堆数学是很悲哀的事情!如果最终你费了九牛二虎之力把数学推理过程搞明白了,你对数学本身的理解将超过你对cdma的理解,本来数学仅仅是为了帮忙理解cdma,可是最终却反客为主了。我认为理解一个概念最好不要从数学开始,数学化的东西只是一个总结,一种表述方式罢了,正如音乐的实质不在五线谱原理和简谱助记法而在旋律本身一样,我敢肯定任何科学理论的提出都不是从数学开始的,但是却总是归于数学,正如任何伟大的音乐作品只从音乐本身开始,伟大的美术作品的作者不需要事先研究配色原理一样。记住,数学只是工具!
一.开始吧,从吉普赛纸牌开始
小的时候,我们都玩过吉普赛纸牌,用来算自己某天会不会有“桃花运”,这种纸牌算出来的桃花运像魔咒一样,使腼腆的你对你喜欢的小女孩说“我喜欢你”(我就这么玩过,结果很尴尬...),不知道为什么这种游戏现在没有人玩了。表面上每张牌上写满了乱七八糟的文字,如下图:

然而当你用一张挖有小洞的纸牌罩在写满字的纸牌上的时候,你会发现上面写着一句话,如下所示:

这种游戏也许和我们现在玩的《愤怒的小鸟》之类的相比有点傻,然而它确实是一个古老的游戏,本文的目的不是为了揭示游戏原理,而是它有助于我们理解cdma。
我们把写满文件的纸牌看做是“仅有一个有效信号,其它对于接收者来讲全是噪音”的叠加信号,而挖有小洞的纸牌就是分配给每一个人的“码”,每一个“码”都不同,因此当用这些码罩到叠加信号上时,能显示出的只是我们感兴趣的信息,比如“你有桃花运”。就这么简单,所有的信号尽管发过来好了,我不怕干扰,因为我用我的“码”可以解出发给我的信息。
显然,如果一张牌上能写100个字,每句有意义的话有5个字,那么我们就可以设计出20张挖有小洞的纸牌作为“码”,每张纸牌上有5个洞,能通透5个字。如果没有“码”,100个字看起来就是乱码,因此这种方式还起到了一定的信息加密的作用。20个码分给20个人,就可以通信了,在和对方交换信息前,先用对方的码把信息填到相应的位置,对方收到后就自己的码往纸牌上一罩,结果就出来。
所谓的码分多址最终就归于一副吉普赛纸牌上。很简单吧
二.好吧,再看看别的例子
除了吉普赛纸牌,其实我们每天都在接触码分多址:
1.大学刚开学的时候,军训时,在火车上,飞机上,大家聊天时,你能一耳朵听出谁是你的老乡,因为有时候别人使用的方言你根本听不懂,也就是说你没有理解那种语言的“码”,我们的大脑中天生拥有一种过滤母语或者方言的“码”!
2.长途旅行中,你很困,旁边的两个家伙叽叽喳喳说个不停,如果他们使用你听不懂的语言,你照样能睡着,但是如果他们说的是普通话,那你就完蛋了,那就忍耐吧
三.该我们自己设计了
大自然已经设计了我们的大脑这种高度复杂的“码分多址设备”,我们当然使用这个设备也能造出一个克隆体,如果我们就是上帝,那么我们希望造出和我们一样的东西,因此码分多址技术是必然要出现的,如果你不承认它是一种创意,起码它也是我们自身的印照!
通过吉普赛纸牌,我们发现,码分多址的要点在于诸多的“码”本身是不能互相干扰的“掩码”,它有两个特点:
一是码之间两两不能互相干扰(因为不能在纸牌的一个位置写下两个不同的字);
二就是它们是掩码,所谓的掩码就是将不需要的信息“掩去”。
这就是要点,我们只要能设计出类似的编码规则就可以了,这难道很难吗?
理解了上述的“码”的两个基本特征之后,接下来再考虑数学实现也不迟,我当然还是试图不使用数学,期望在全文中不提什么“沃尔什函数”,“正交”,“卷积”之类的概念,可是我觉得还是有必要阐述一下,因为第一,正交的概念真是太美了,一下子就把上述两个特征都实现了;第二,不使用那些复杂的推导过程也能理解上述的数学概念,没有学过微积分和矩阵原理也没有问题。
四.为什么需要数学
任何领域几乎都需要数学,数学确实是一个好东西,它不仅仅是一种工具,它还是一种大脑训练操。因为它足够抽象,能够很方便的建模,使各领域的设计师将精力集中在该领域本身,纯逻辑和纯理论抽象的部分交给数学来解决,由于现代数学是建立在一整套很严密的逻辑的基础上的,因此它的结论一般不容置疑(当然不要考虑哥德尔考虑的问题,那是数学家和逻辑学家的工作),而且在数学推理过程中,可以排除特定领域的概念干扰,比如在基于牛顿第二定律计算运动物体速度时,可以排除接触面粗糙程序,阻尼等物理概念。数学完全符合高内聚低耦合的特征,因此虽然数学看起来很令人讨厌,然而当你熟悉了它之后,它真的很有趣!能使我一心一意工作的诱惑有两个,一个是加薪,另一个就是数学,真的是这样(虽然平时不怎么使用数学,然而数学带来的不是知识本身,不是会背几个公式知道几个名词,值得享受的是思考的过程和从中总结出的“道”)。
然而切记,只有两种情况下使用数学,一种是你在体验数学本身,二是你使用它描述或者解决问题,并且此时你已经彻底理解了问题的本质。(有些顶级草根黑客认为代码需要想到及写出,然后慢慢修改调试,正如画油画一样,而大部分公司的经理却厌恶这种论调,他们总希望你在编码之前先提交一堆文档,然后等到最后再用最短的时间编码,这也许就是艺术和技术的区别吧?)
五.先从最简单的情况看起
如果问一个初中生,力是如何合成的,如何分解的,他会马上说出矢量,正交,坐标系,cos,sin等概念,既然初中生都明白力是怎么合成的,那么咱们作为一群大学都毕了业好几年的家伙,怎能不知呢?你如果否定,那既然你知道力是如何合成和分解的,怎么就不能理解码分多址呢?
考虑最简单的只有两个码的码分多址中,叠加的信号就是一个两个个力的合力矢量,而特定用户解出的属于自己的信息就是该合力在一个坐标轴上的分力,他们使用的“码”就是坐标轴上的单位矢量,且坐标轴是正交的(相互垂直的笛卡尔坐标系)。如下图:

很简单吧,实际上也真是这么简单。回忆吉普赛纸牌,是不是很一致呢,我们可以设纸牌上可以写20个字,一个作为码的纸牌上可以挖10个洞,只要两张挖洞纸牌上的洞的位置不重合,那么可以认为这两张挖洞纸牌就是正交的。第二个特征是掩码,实际上可以通过正交推理出来,因为正交概念本身就是井水不犯河水的关系,顺着笛卡尔坐标系的x轴向原点望去,你只能看到y轴,而看不到x轴,反过来沿着y轴向原点看,你也只能看到x轴,是不是掩码的意思呢?一个正交的概念解决了两个问题。如下图:

以合力解释这个叠加信息的编码是很容易理解的,合力仅仅是实际力的合成,是实际力-垂直力和水平力的承载体,以力的效果来说明它们互相不干扰就是:水平力不会造成物理在垂直方向有位移,垂直力也不会造成物体在水平方向有位移,应用在信息上,用户A使用码X编码的信息i1和用户B使用码Y编码的信息i2最终叠加成了I,也就是合力,然而某一用户如果使用码X将信息I分解,它得到的将是i1,对i2丝毫没有影响,为什么呢?因为码X和码Y是正交的,正如上述的X轴和Y轴正交一样。
六.稍微扩展一点正交,没想到,就这样结束了
归纳能力是人类特有的能力,有趣的是,人们归纳曾经发生的过事的目的恰恰是为了预测未来的事。笛卡尔坐标系是欧几里得空间的正交系,它可以解决和解释大量的问题,然而直到17世纪,数学仍然没有作为一个独立的学科发挥巨大的作用,原因正是到那时为止,数学太形象化了,直到微积分和希尔伯特空间被提出来,数学才从具体的学科中被抽出来,专门向更抽象和逻辑性更强的方向发展。这种发展最终反过来影响着具体的学科,受其影响最大的学科就是物理学和信息学了。
如果大家理解了上述的枝枝蔓蔓,此时就可以一头扎进数学了,但是注意,千万不要恋战,点到为止,再次重申,数学只是工具,除非你想专门研究它!
既然二维的笛卡尔正交系可以抽出两个正交量从而形成两个所谓的“码”,那么如果有一个正交系有N个正交量,那么不就是说有N个“码”了吗?是的,确实正确!并且这样的正交系是存在的,数学作为工具在此发挥了作用。
要讲述正交的概念,很多教科书本着先导出概念的原则先讲述了向量,然后讲述了内积之类的概念,最终告诉你内积为0的两个向量是正交的,当你得到这个答案的时候,你可能已经被内积以及之前的概念搞糊涂了,或者已经厌烦了,已经忘记了当初为何需要知道什么是正交,以及需要正交的哪些性质,因此这种教育方式对于喜欢科学探索的家伙来讲无疑是毒药!什么是正交呢?简单点说两个正交量肯定是相交的,也就是有联系的,但是这种联系很“正”,也就是除了在交点发生关系之外,其它哪里都不发生关系,只要满足这两点都是正交的量,对于二维空间,直角坐标系的x轴和y轴在原点相交,它们又彼此垂直,彼此在对方没有任何分量,因此它们正交。对于超过3个的多个量,只要满足“相关联”,“关系很正”这两个性质都属于正交量,因此理解了这一步,我们看看数学语言是如何描述它的,对于连续量,使用积分来描述,对于离散量来讲,就更简单了,如果我们设空间有M个分量,那么一个向量将表示为:

这就是多维空间的正交向量,就这么简单。如果我们把这样的向量作为“码”分给每一个用户,那么用户用这个向量码和自己的标量信息做一个算术乘法,作为结果Rn,Rn显然也是一个多维向量,然后所有的用户的这些Rn加在一起:R1+R2+...Rm,最终形成一个M维空间的向量,这就相当于一个合力,信息到达接收端后,用户只需要将“合力”分解到自己的“码”上就可以了,注意,为了使运算简单,最好使用单位向量作为码。
六.构造多维正交向量
原理就是这么简单,可是我们怎么去构造这么一组向量满足式子(1)然后从而分配给用户呢?如果你独自思考问题到了这个地步,接下来你要干什么你自己就很明了了,如果你觉得你是个天才,你就去自己去想个办法,如果你觉得你只是想弄明白cdma的原理或者在搞一个新的编码或者别的,那么你肯定去阅读相关的数学资料了。看到了吗?我们第二次使用数学,前一次搞明白了希尔伯特空间向量,这次我们需要搞到一个简单的,且能得到多个正交的向量的方法,是什么呢?哎,最终还是要提到沃尔什函数,Ahha!
还是我的老原则,那就是先看效果,然后反思,或者说试图从一个巨人的脚后跟往上爬,最终爬到另一个巨人的肩膀!好了,先看一眼沃尔什向量长什么样子吧:
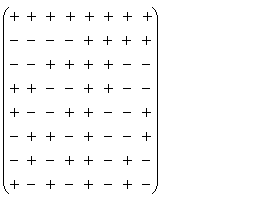
【和大多数教科书一样,我将“1”换成了“+”,将“-1”换成了“-”,沃尔什矩阵中只有“1”和“-1”】
不管怎样,先不管它的原理,看看任意两行或者任意两列,显然是正交的,完全符合需求,然后,和那个力的合成和分解一样,就算就可以了,超级简单,在理解原理前,我们先看看如何进行cdma的核心编码,当我们发现其简单性之后,再来考虑原理,最终我们会为这一切配合的如此完美而叹为观止!
七.沃尔什编码的简单性使得CDMA大有前途
沃尔什矩阵如何编码数据呢?我们知道数据都是0和1组成的,这就更好办了。首先为每一个用户分配一个N阶沃尔什矩阵中的一行或者一列(要么全是行要么全是列),将数据的0,1序列和向量相乘,这是纯粹是标量和向量的乘法,乘以分量即可,...(当然事实上没有这么简单,编码问题什么时候都是很复杂的,然而本文主要帮助大家理解cdma的本质,而不是研究如何编码)。我以一个实例结束核心讨论:
1.用户1的码:a1=(-1 -1 -1 -1 1 1 1 1)--第2行
2.用户2的码:a2=(-1 1 -1 1 1 -1 1 -1)--第7行
3.用户1的数据:d1=110
4.用户2的数据:d2=010
下面开始编码过程,假设发给用户1和用户2的数据叠加在一起,用户1的数据最终成为:
(-1 -1 -1 -1 1 1 1 1)|(-1 -1 -1 -1 1 1 1 1)|(0 0 0 0 0 0 0 0)【前面的|隔开的是用户1的三位数据编码后的结果,每一位用户数据都是标量,和码相乘,结果还是向量】;用户2的数据最终为:
(0 0 0 0 0 0 0 0)|(-1 1 -1 1 1 -1 1 -1)|(0 0 0 0 0 0 0 0),二者叠加后为:
(-1 -1 -1 -1 1 1 1 1)|(-1 -1 -1 -1 1 1 1 1)|(0 0 0 0 0 0 0 0)
(0 0 0 0 0 0 0 0)|(-1 1 -1 1 1 -1 1 -1)|(0 0 0 0 0 0 0 0)
_______________________________________________________________
(-1 -1 -1 -1 1 1 1 1)|(-2 0 -2 0 2 0 2 0)|(0 0 0 0 0 0 0 0)
最终结果是:
(-1 -1 -1 -1 1 1 1 1)|(-2 0 -2 0 2 0 2 0)|(0 0 0 0 0 0 0 0)
这个叠加的数据同时到达用户1和用户2,用户1解码的过程实际上是一个“力的分解”过程,如果是二维的情况,如果我们知道有一个“合力”是(a b),那么要求在x轴上的投影向量,我们该怎么办?其实我们不必求投影向量,只求投影的长度即可,毕竟被编码的数据是标量啊!这就更简单了,随便问一个初中生估计能得到最简单的答案。答案就是:L乘以夹角的余弦值!
然而对于多维向量而言,L是不易的,因为多维向量不好用【勾股定理】(我更喜欢用毕达哥拉斯定理这个词)。那么怎么办呢?向量的事最好由向量自己解决,记住,有很多我们中学时学习到的定理或者公式都是不适合高维空间的,毕竟那是古人经验(计算车轮子的长度,计算横梁)或者纯思辨哲学(苏格拉底,柏拉图,亚里士多德的时代)的成果,那时数学还没有抽象到希尔伯特时代的程度,因此我们还是用现代的方法吧!现代的方法为:

所以忘掉中学时的知识吧。如果我不进一步说明上述的公式是怎样导出的,我还是落入了俗套,因此,我给出简单的推导,哪怕是一点指点迷津的思路也行:

起初数据为k,然后和数据r一起被编码并且叠加在一起,最终又恢复了k,一切使用的都是矩阵的加法和乘法运算,最幸运的是,这些运算都是很简单的。
CDMA的本质理解了吗?实际上,这种方式如此简单的解决了码分多址编码问题,使用了这种方式之后,可以巧妙绕开那些相对复杂的变换或者逼近,比如傅里叶变换和离散余弦变换,因为再也不需要那种方式了,使用CDMA的方式可以使得频谱越宽越有效,而且再也不用靠增加功率来传输信号啦,扩频通信由来于此!
那么沃尔什矩阵究竟是怎么来的呢?可能是沃尔什本人靠他天才的大脑想出来的,也可能...最重要的是,如果理解了哈达玛矩阵的话,理解沃尔什矩阵就简单多了,因为哈达玛矩阵是沃尔什矩阵的一种表述方式,它的最重要的特征就是其递推性,从低阶的矩阵可以推导出高阶的,而且生成原则很简单,仅凭如此它就比其它的编码方式更具优势,更别说它的码分多址特性了。
八.凯撒加密和扩展的凯撒加密
在古代,如果手持一张羊皮纸,上面写着乱七八糟的文字,然后如果有一个人拿着一张打着窟窿眼的羊皮贴到写字的羊皮上之后,就能复原信息,窟窿眼在不同的位置,信息呈现就会有所不同,这是一种数据加密的方式,同时也是一种数据复用的方式,这叫什么呢?其实这就是码分多址啊!因此码分多址天生就和加密不可分,这种编码方式天生具有安全性,究其深层原因,实质在于“码”本身参与了编码,而码是特定区间内用户唯一的,这个码可以理解成密钥,也可以理解成收发方作为一个整体共享的私钥!
彻底理解了码分多址的本质之后,发现它的简单性以及优美原来来源于它靠向量本身编码,我们提到向量觉得起码得要二维才行,实际上我们更希望从1开始,想想看,一维数轴上的数字难道不是向量吗?如果我们使用一维的向量来进行编码,实际上就会发现这原来就是扩展的凯撒加密运算。
什么是凯撒加密呢?简单的说,凯撒加密需要一个10进制的数字k作为密钥,然后初始信息的每一个字母编码为其在字母表中位置加上k的位置处的字母。
扩展的凯撒加密就是使用一个序列a1,a2,a3,...aM作为密钥,然后将待加密的字母序列中每一个字母bN编码为字母表中其所在位置加上aN的位置处的字母,是不是和本文开始处的吉普赛纸牌很相似呢?没有挖洞的吉普赛纸牌我们看不懂写满文字的吉普赛纸牌中的信息含义,因此吉普赛纸牌天生就有保密性的特性,且它和凯撒加密法又是如此相似,并且,更简单的一个例子,如果一个吉普赛人在中国大骂,我们十有八九听不懂他们的话,依然会微笑!
No comments:
Post a Comment