http://frankliou.wordpress.com/2012/02/24/%E6%9F%AF%E8%A5%BF%E5%88%97%E5%AE%8C%E5%82%99%E5%8C%96/
賦距空間的完備化
二月 24, 2012
完備化的基本定義
令取
(柯西列)定義:如果對任意的
收斂序列是柯西列,反之是否Cauchy列是否為收斂序列?我們先來看以下的例子,了解到一般的賦距空間中的柯西列未必是收斂數列。
範例1.令數列
(完備空間)定義:如果一個賦距空間的所有Cauchy列都是收斂序列,則我們稱此賦距空間為完備的賦距空間(complete metric space)。
完備空間是相當重要的,因為我們希望透過利用空間中的Cauchy列去建構某種方程(線性或非線性微分或積分方程)的解。例如,我們希望建立積分方程
的解。如果你的空間不是完備的,那麼利用柯西列去構造方程的解便沒有任何意義。但幸運的是,所有的賦距空間 都包含於某個更大的完備賦距空間中。如果
都包含於某個更大的完備賦距空間中。如果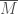 是包含
是包含 的完備賦距空間,並且
的完備賦距空間,並且 是
是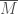 的稠密子集,則我們稱
的稠密子集,則我們稱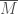 是
是 的完備化(completion)。在進入完備化空間的數學定義之前,先讓我們熟悉一些賦距空間中的基本定義。
的完備化(completion)。在進入完備化空間的數學定義之前,先讓我們熟悉一些賦距空間中的基本定義。
(保長映射)定義:假設(賦距空間的同構)定義:如果存在一個一對一且映成的函數
附註:我們可以定義一個關係如下:任給兩個賦距空間
(稠密)定義:令
(完備化)定義:令
(1)
(2)
命題:如果
(完備化)定義:令
說明:為了方便起見,通常我們會把
完備化空間的建構
令
不難証明 是一個等價關係(equivalence relation)。給定一個Cauchy 列
是一個等價關係(equivalence relation)。給定一個Cauchy 列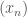 ,我們記
,我們記![[(x_{n})] [(x_{n})]](http://s0.wp.com/latex.php?latex=%5B%28x_%7Bn%7D%29%5D&bg=ffffff&fg=444444&s=0) 為所有與
為所有與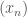 等價的柯西列所成的集合。令
等價的柯西列所成的集合。令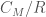 是所有
是所有 等價類所成的集合。我們稱
等價類所成的集合。我們稱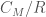 為此等價關係的商空間(quotient space)。在這個集合上,我們定義一個函數
為此等價關係的商空間(quotient space)。在這個集合上,我們定義一個函數 如下
如下
命題:
如果
命題:
重要的範例
令範例1.(
範例2.(Sobolev 空間)在
No comments:
Post a Comment