Everett (╮(╯▽╰)╭ ~(= ̄ U  ̄=)~) 2010-01-13 19:29:29
2010-01-13 14:12:35 断雁嵬蝶
哦,我有个地方也不太清楚,二次量子化后描述态的应该还是波函数吧?
=====================
是的,二次量子化以后,波函数就升级为“波泛函”了。Wave functional? 嗯,我又民科了,这个词是我生造的 :-)……
所谓量子化就是一个确定性丧失的过程。在一次量子化中,所有物理量的确定性都丧失了。形式上看,就是物理量从确定的数,变成不确定的算符。但是一个算符挂在空中摆来摆去是没有意义的。只有当算符落实到波函数上的时候,它才能获得意义。所以波函数的引入,对于一次量子化来说,是显然而且必须的。波函数是关于粒子状态的函数,取值为复数,其模方表示粒子出现在该状态的几率。从此,一切物理量都依概率分布,我们再也不能问“能量是多大”,只能问“能量是这么大的概率是多少”。
但是一次量子化并不是一场彻底的革命。有两个物理量仍然是确定的,是可以测准的:一个是几率本身,另一个是作为相位的作用量。它们合在一起可以构造出波函数。既然一切物理量都不确定了,那么为什么只有概率分布还是确定的?概率分布为什么不能也依概率分布?因此,二次量子化就是要继续这场革命,将不确定进行到底,剥夺波函数的确定性,把波函数算符化,使之成为场算符。
但是场算符本身也是没有意义的,因为任何算符都不能独立存在,场算符最终也要落实到一个对象上去。但那不是波函数,因为场算符本身就代表波函数,因此场算符应该作用在更高级的波函数上,那就是波泛函 Ψ。
波泛函是一个从Hilbert空间向复数域的映射,Ψ[φ] 把场的每种经典构型 φ(x) (也就是波函数),映射到一个复数 Ψ 上。这个复数就描述了出现φ(x)那种波函数的几率幅,因此可以说是几率之几率。所有的波泛函构成一个更大的“Hilbert空间”。
基于这种构造,我们还可以实施第三次量子化,就是把波泛函再正则量子化为泛函场算符。这样这些场算符同样需要落实。它们作用在“波泛泛函”上面。如此递推,可至无穷。
事实上,从量子力学开始第一次量子化的时候,它就已经蕴含了以后所有阶次的量子化。有了一次量子化就会有二次,有了二次就会有三次。所谓,道生一,一生二,二生三,三生万物。因此,量子力学从原则上讲是一个无穷次量子化的理论,这样的理论中再也没有任何的确定性,因为任何一阶的波函数都会在下一次量子化中被算符化。世界的本质应该是非决定论的,终极的物理学应该是确定性的完全丧失!
那么为什么我们还整天在一次量子化的框架下计算波函数,忙得不亦乐乎?因为,这是一种合理的近似。人们已经在许多场论模型中认识到,量子场的维数越高,量子涨落的效果越弱。每一次量子化,都使场的维度升高一个aleph number。因此很快,量子涨落就会被弱化,于是我们可以做经典近似。就是说,在某次量子化的时候来个截断,用波函数来取代场算符。这样就有了我们常用的一次或二次量子化。
但是我们要记住的事情是,不管是几次量子化都是一种经典近似,都是一定截断下的有效理论。在必要的时候,我们要把这个截断推向更高阶,以获得更好的结果。我们已经知道,平衡态统计力学是Wick转动下二次量子化的量子场论。平衡统计的一个基本观点是认为,平衡系综里面的系统服从Gibbs分布。但是现在我们遇到新问题了,那就是非平衡统计。非平衡统计可以看成是很多个不同版本的平衡统计在依概率分布。因此,统计的对象不再是系统了,而是系综本身。我们要问系综是如何在“系综综”里面分布的?这就是第三次量子化,非平衡是三次量子化的效应。令人感叹的是,三次量子化居然是在统计力学中首先实现,而不是在量子力学,可见量子与统计的某种关系应该是非常深刻的。
艾禮富數[编辑]
维基百科,自由的百科全书
| 各种各样的數 | ||
| 基本 | ||
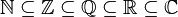
| ||
| 延伸 | ||
| ||
| 其他 | ||
 = 3.141592653… = 3.141592653…自然對數的底  = 2.718281828… = 2.718281828…虛數單位  = =  無窮大  |
可數集(包括自然數)的勢標記為
 ,下一個較大的勢為
,下一個較大的勢為 ,再下一個是
,再下一個是 ,以此類推。一直繼續下來,便可以對任一序數 α 定義一個基數
,以此類推。一直繼續下來,便可以對任一序數 α 定義一個基數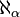 。
。這一概念來自於格奧爾格·康托,他定義了勢,並认识到無限集合是可以有不同的勢的。
阿列夫數与一般在代數與微積分中出現的無限 (∞) 不同。阿列夫數用来衡量集合的大小,而無限只是定義成實數線上的最大的極限或擴展的實數軸上的端點。某些阿列夫數會大於另一些阿列夫數,而無限只是無限而已。
構造性定義[编辑]
阿列夫數的直觀定義並沒有解釋什麽叫“下一個較大的勢”,也沒有證明是否存在“下一個較大的勢”。即便承認對任意的基數都存在更大的基數,是否存在“下一個較大的勢”使得這個基數和“下一個較大的基數”之間不再有其他的基數仍然是個問題。下面的構造型定義解決這個問題:[1]:28- ℵ₀ 定義從前,它是一個良序集 ℕ 的序數;
- 考慮良序集[1]:25按照某种同構關係[注 1]划出的等價類[1]:18[注 2];
- 如上定義的等價類有一個特點:可比較[1]:25,
- 設 ℵₐ 已定義且是一良序集的基數,考慮:
數“阿列夫”[编辑]
在中國大陸,實數集的基數常被記爲 c 或 ℵ,卽 ℵ := ℶ₁,這樣連續統假設就常常被表述爲 ℵ = ℵ₁.閲讀相關讀物時應避免混淆。人們在學數學分析(微積分)時常常以爲自己時常遇到的是阿列夫数,事實上他們遇到的是 “ℵ”或“c”,卽角標爲1的 ℶ 數。除非討論集合論,否則阿列夫数將是最不常用的基數之一Aleph number
From Wikipedia, the free encyclopedia
"Aleph One" redirects here. For other uses, see Aleph One (disambiguation).
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality (or size) of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph (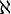 ).
).The cardinality of the natural numbers is
 (read aleph-naught, aleph-null, or aleph-zero), the next larger cardinality is aleph-one
(read aleph-naught, aleph-null, or aleph-zero), the next larger cardinality is aleph-one  , then
, then  and so on. Continuing in this manner, it is possible to define a cardinal number
and so on. Continuing in this manner, it is possible to define a cardinal number 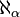 for every ordinal number α, as described below.
for every ordinal number α, as described below.The concept goes back to Georg Cantor, who defined the notion of cardinality and realized that infinite sets can have different cardinalities.
The aleph numbers differ from the infinity (∞) commonly found in algebra and calculus. Alephs measure the sizes of sets; infinity, on the other hand, is commonly defined as an extreme limit of the real number line (applied to a function or sequence that "diverges to infinity" or "increases without bound"), or an extreme point of the extended real number line.
想问个外行的问题,量子场论和量子力学是什么关系...


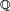
![\begin{smallmatrix} \mathbb{Z}[i] \end{smallmatrix}](http://upload.wikimedia.org/math/5/2/2/522c8c20a747acc35a997e5f1e3e2b7f.png)
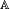

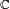
![\begin{smallmatrix} \mathbb{Z}[\omega] \end{smallmatrix}](http://upload.wikimedia.org/math/2/8/0/280b4c450c08bf8046ebcc5b55220b9c.png)

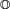



No comments:
Post a Comment