線代啟示錄
I seek not to know the answers, but to understand the questions.

梯度、旋度與散度
本文的閱讀等級:初級
向量算子是向量分析 (vector calculus 或 vector analysis) 的馱馬,最重要的算子包括梯度 (gradient)、旋度 (curl) 和散度 (divergence)。令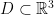 是一開集,
是一開集, 是一次連續可微函數 (以
是一次連續可微函數 (以 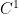 表示),且
表示),且 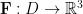 是定義於
是定義於 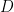 的一
的一 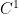 向量場 (vector field)。所謂向量場其實就是一個向量函數,例如,
向量場 (vector field)。所謂向量場其實就是一個向量函數,例如,
 ,
有些物理和微積分課本將向量場
,
有些物理和微積分課本將向量場  表示為
表示為
 ,
其中
,
其中 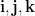 是
是 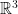 的標準單位向量 (線性代數慣用的對應記號為
的標準單位向量 (線性代數慣用的對應記號為  )。為便利表達,我們將微分算子
)。為便利表達,我們將微分算子  (讀作nabla) 視為一向量:
(讀作nabla) 視為一向量:
![\displaystyle \nabla =\begin{bmatrix} \frac{\partial }{\partial x}\\[0.3em] \frac{\partial }{\partial y}\\[0.3em] \frac{\partial }{\partial z} \end{bmatrix}=\begin{bmatrix} D_x\\ D_y\\ D_z \end{bmatrix} \displaystyle \nabla =\begin{bmatrix} \frac{\partial }{\partial x}\\[0.3em] \frac{\partial }{\partial y}\\[0.3em] \frac{\partial }{\partial z} \end{bmatrix}=\begin{bmatrix} D_x\\ D_y\\ D_z \end{bmatrix}](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cnabla+%3D%5Cbegin%7Bbmatrix%7D++%5Cfrac%7B%5Cpartial+%7D%7B%5Cpartial+x%7D%5C%5C%5B0.3em%5D++%5Cfrac%7B%5Cpartial+%7D%7B%5Cpartial+y%7D%5C%5C%5B0.3em%5D++%5Cfrac%7B%5Cpartial+%7D%7B%5Cpartial+z%7D++%5Cend%7Bbmatrix%7D%3D%5Cbegin%7Bbmatrix%7D++D_x%5C%5C++D_y%5C%5C++D_z++%5Cend%7Bbmatrix%7D&bg=ffffff&fg=000000&s=0) ,
這裡
,
這裡  是偏微分算子。函數
是偏微分算子。函數  的梯度 (grad),向量場
的梯度 (grad),向量場  的旋度 (curl) 和散度 (div) 定義如下:
的旋度 (curl) 和散度 (div) 定義如下:
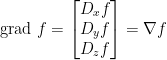

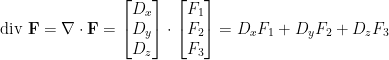 。
旋度和散度的定義很容易混淆,初接觸時不妨用助記術來聯想:旋度 (curl) 和外積 (cross product) 的第一個英文字母都是「c」,散度 (div) 和內積 (dot) 的第一個英文字母都是「d」。通過微分形式 (differential form) 和外微分 (exterior derivative) 可以幫助我們理解這些向量算子的幾何意義,在此不深入討論,本文僅利用行列式和基礎向量運算推導梯度、旋度和散度的一些恆等式。
。
旋度和散度的定義很容易混淆,初接觸時不妨用助記術來聯想:旋度 (curl) 和外積 (cross product) 的第一個英文字母都是「c」,散度 (div) 和內積 (dot) 的第一個英文字母都是「d」。通過微分形式 (differential form) 和外微分 (exterior derivative) 可以幫助我們理解這些向量算子的幾何意義,在此不深入討論,本文僅利用行列式和基礎向量運算推導梯度、旋度和散度的一些恆等式。
我們可以從 Jacobian 矩陣得到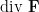 和
和  (見“Jacobian 矩陣與行列式”)。向量場
(見“Jacobian 矩陣與行列式”)。向量場  的 Jacobian 矩陣為
的 Jacobian 矩陣為
 。
觀察得知
。
觀察得知  。寫出
。寫出  的卡氏分解
的卡氏分解 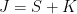 ,其中
,其中 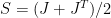 是對稱部分,
是對稱部分,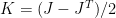 是反對稱部分,如下:
是反對稱部分,如下:
 。
觀察發現
。
觀察發現  的三個元
的三個元 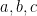 即為
即為 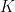 的下列對應元:
的下列對應元:
![\displaystyle K=\frac{1}{2}\left[\!\!\begin{array}{rrr} 0&-c&b\\ c&0&-a\\ -b&a&0 \end{array}\!\!\right] \displaystyle K=\frac{1}{2}\left[\!\!\begin{array}{rrr} 0&-c&b\\ c&0&-a\\ -b&a&0 \end{array}\!\!\right]](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle++K%3D%5Cfrac%7B1%7D%7B2%7D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Brrr%7D++0%26-c%26b%5C%5C++c%260%26-a%5C%5C++-b%26a%260++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0) 。
。
另一個方式是透過行列式運算。令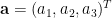 ,
, ,
, 。為方便書寫與計算,我們將外積
。為方便書寫與計算,我們將外積  以行列式表示為
以行列式表示為
 。
注意,在計算行列式時,向量
。
注意,在計算行列式時,向量 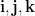 視同純量。同樣地,
視同純量。同樣地,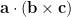 也可以用行列式表示如下 (見“答張盛東──關於外積與行列式的關係”):
也可以用行列式表示如下 (見“答張盛東──關於外積與行列式的關係”):
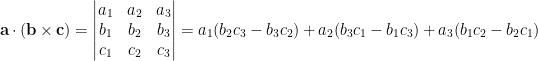 。
。
下面我們運用行列式來推導幾個梯度、旋度和散度的公式。
(1) 對於任一 函數
函數  ,梯度的旋度為零向量:
,梯度的旋度為零向量:
 。
寫出
。
寫出  ,根據定義式,
,根據定義式,
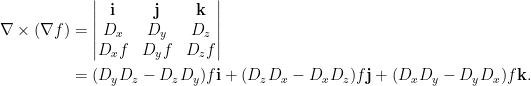 偏微分具有對稱性 (或說可交換性),即
偏微分具有對稱性 (或說可交換性),即  ,故每一項都等於零。
,故每一項都等於零。
(2) 對於任一 向量場
向量場  ,旋度的散度為零:
,旋度的散度為零:
 。
使用行列式表達式,由偏微分的對稱性可推論
。
使用行列式表達式,由偏微分的對稱性可推論
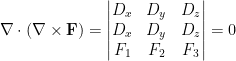 。
另一個較為「激進」的說法是行列式有相同的兩列因此為零。
。
另一個較為「激進」的說法是行列式有相同的兩列因此為零。
(3) 對於任一 函數
函數  ,梯度的散度稱為
,梯度的散度稱為  的 Laplacian:
的 Laplacian:
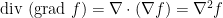 ,
其中 Laplace 算子定義為
,
其中 Laplace 算子定義為  。直接用內積運算可得
。直接用內積運算可得
 。
對於向量場,我們也可以按類似方式定義
。
對於向量場,我們也可以按類似方式定義
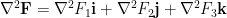 。
。
(4) 對於任一 向量場
向量場  ,
,
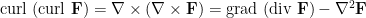 。
這個等式將梯度、旋度、散度和 Laplacian 四個算子聯繫在一起。證明於下:寫出
。
這個等式將梯度、旋度、散度和 Laplacian 四個算子聯繫在一起。證明於下:寫出  ,套用行列式表達式,
,套用行列式表達式,
 上式看似複雜,幸好只要化簡其中一項,利用對稱性即可推得其餘項。直接乘開
上式看似複雜,幸好只要化簡其中一項,利用對稱性即可推得其餘項。直接乘開  的係數或使用行列式餘因子公式化簡,過程如下:
的係數或使用行列式餘因子公式化簡,過程如下:
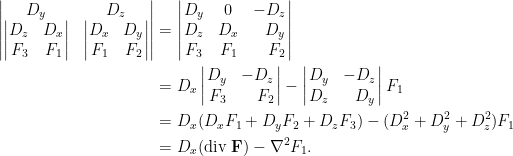 再將
再將 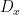 和
和 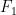 替換為
替換為 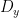 和
和 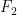 ,以及
,以及  和
和  便得到其他二項。整理結果,可得
便得到其他二項。整理結果,可得
 ,
此即所求。
,
此即所求。
最後我列舉一些常見的向量分析公式,供讀者自行練習證明[1]。以下 是常數,
是常數, 和
和 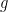 是純量函數,
是純量函數,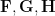 是向量場。
是向量場。
參考來源:
[1] Jerrold E. Marsden 與 Anthony J. Tromba 合著 Vector Calculus,1976,頁166。
向量算子是向量分析 (vector calculus 或 vector analysis) 的馱馬,最重要的算子包括梯度 (gradient)、旋度 (curl) 和散度 (divergence)。令
我們可以從 Jacobian 矩陣得到
另一個方式是透過行列式運算。令
下面我們運用行列式來推導幾個梯度、旋度和散度的公式。
(1) 對於任一
(2) 對於任一
(3) 對於任一
(4) 對於任一
最後我列舉一些常見的向量分析公式,供讀者自行練習證明[1]。以下
,
參考來源:
[1] Jerrold E. Marsden 與 Anthony J. Tromba 合著 Vector Calculus,1976,頁166。
This entry was posted in 特別主題, 主題專欄 and tagged Jacobian 矩陣, Laplace 算子, 外積, 散度, 旋度, 梯度. Bookmark the permalink.
——————–
您文章裡頭談到:
旋度的散度為零,另一個較為「激進」的說法是行列式有相同的兩列因此為零。
我以前也曾經有這個想法,用行列式的性質,一眼看出,它等於零!
但是所看過幾本向量分析的書,皆沒這樣寫。
大概是我看過的書不多吧!
我不知道,是否有哪一本向量分析的教科書,真的這樣寫?
——————–
另外,維基百科談「旋度」
https://zh.wikipedia.org/wiki/%E6%97%8B%E5%BA%A6
有一句話,行列式記號只有形式上的意義,因為真正的行列式中的係數應該是數,而不是i, j, k這樣的向量。這種表示方法只是便於記憶旋度在直角坐標系中的表達式。
我看到這句話,思考著,行列式裡,真的必需存放「數值」嗎?運算子放在行列式之中,只是方便記憶嗎?
我所知道的,像是牛頓與萊布尼茲的微積分,經過三百餘年,Weierstrass與Cauchy等人,作了嚴謹證明。
歐拉的著作,原本份量已不少,原書的許多地方僅是輕描淡寫。有人用詳細論證方式,重新演算,變成更厚之巨冊。
另外,複數域的自然指數Exp(z)還沒證明,(我忘了是哪位數學家) 竟然把它比照實數域的Exp(x)使用,這是不是很「危險」?很「不嚴謹」?萬一錯了怎麼辦?幸好還能算出答案,早年卻沒有證明。後人發展「複變函數論」,才真的證明Exp(z)的微分、積分等各種性質,不僅表達式與實數域的Exp(x)相似,也是可靠的!
這回在老師的部落格談到,微分運算子放在行列式裡頭,div (curl F) 的演算,兩列微分運算子相同,由行列式的性質可知,行列式值為零。雖然「不嚴謹」,看起來卻是一種幫助「認知」的好方法。
以上這些,我想表達,數學教育,有時太過於著重「嚴謹」,而使學生畏懼。
如果先享受「概念式」學習,然後,有興趣詳細研究的人,可以升級到「嚴謹」階段。循序漸進教學,可以讓更多人喜歡數學。
我常來周老師的部落格瀏覽,就是喜歡看看「不一樣」的論述方式,得到許多靈感啟發!
感謝老師持續寫作,嘉惠許多學生。