phymath999: 系统初始态是一个退耦合纯态。态矢为甲

Sunday, May 4, 2014

系统初始态是一个退耦合纯态。态矢为甲

混合態量子系統出現的案例包括，處於熱力學平衡或化學平衡的系統、製備歷史不確定或隨機變化的系統（因此不知道到底系統處於哪個純態）。假設量子系統處於由幾個糾纏在一起的亞系統所組成的純態，則雖然整個系統處於純態，每一個亞系統仍舊可能處於混合態。在量子退相干理論裏，密度算符是重要理論工具。
密度算符是一種線性算符，是自伴算符、非負算符（nonnegative operator）、跡數為1的算符。關於密度算符的數學形式論是由約翰·馮·諾伊曼與列夫·郎道各自獨立於1927年給出。^[1]^[2]^:48-55^[3]

问题：叠加态和混合态有何区别？_相对论吧_百度贴吧

tieba.baidu.com/p/1054314870‎
轉為繁體網頁

2011年4月17日 - 我的理解就是，因为给定的纯态态矢并不一定正交，所以当某个态是多个纯态的混合，但却并没有相干项的时候，这个态就不能用希尔伯特空间里的 ...

（理论物理专业优秀论文）两个二能级原子与单模真空场相互 ...

www.docin.com › 论文 › 毕业论文‎
轉為繁體網頁

2011年12月2日 - 系统初始态是一个退耦合纯态。态矢为甲（o））爿L。（o）徊l□（o））＝｜＋＋o）（3．4）在相互作用绘景中，任意时刻t＞0，系统的态矢随时间的演化 ...

基于量子反馈的量子态调控方案研究_CNKI学问

xuewen.cnki.net/CMFD-1012399780.nh.html‎
轉為繁體網頁

量子信息理论 ·量子跃迁 ·最大纠缠态 ·零差探测 ·相干性 ·量子相干 ·量子纠缠 ·密度算子 ·激发态布居数 ·纯态 ·态矢空间 ·混合纠缠态 ·消相干 ·entanglement ·反馈方案 ...

光子纠缠与量子通信- 硕士论文- 道客巴巴

www.doc88.com › 所有文档 › 学术论文‎
轉為繁體網頁

2012年5月3日 - 为了更好的理解经典比特和量子比特的区别，我们可以参考图2．1，图中的Bloch球，从始于球心，指向球表面一点的矢量对应一个纯态态矢，球表面 ...

[PDF]

下载 - 上海交通大学

ccs.sjtu.edu.cn/gfile.php?dt=f&id=458‎
轉為繁體網頁

稳定态的热光场。按照密度算符理论，描述处于混合态的光场的密度算符定义为： i i i i. P ρ ψ ψ. = ∑. （2-12）. 式中 i ψ ——归一化的光场纯态态矢； i. P ——光场处于 ...

[DOC]

葉公杼

psroc.phys.ntu.edu.tw/bimonth/download.php?cpid=133&d=2...‎

量子資訊科學是物理學與資訊科學相結合的一個新興交叉領域，涉及物理、數學、 ... 如果我們用量子力學中兩個互相獨立正交的量子態，如光子的兩個極化態、或電子、 ...

[PDF]

慢光與光儲存在量子資訊科學之應用

psroc.phys.ntu.edu.tw/bimonth/v30/524.pdf‎

光速減. 慢甚至完全停止所衍生的光儲存（storage of light）. [17-21]也提供了光子與原子交換波函數或量子態的方. 法[22-24]，這些研究對量子訊息的操縱有重大的影響.

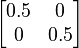$\begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \\ \end{bmatrix}$ 。

通過垂直平面偏振器（3）之後，光子處於垂直偏振純態（4），密度矩陣為

$\begin{bmatrix} 1 & 0 \\ 0 & 0 \\ \end{bmatrix}$ 。

純態（pure state）這個名詞出現在幾個領域，包括物理方面的量子力學以及數學方面的泛函分析理論。

量子力學[编辑]

在量子力學當中，純態由一個相同統計系綜(ensemble)所構成，而相對於純態的混態(mixed state)則可以分解兩個以上的系綜。在量子力學中有諸多表示型(formalism)，一個量子態可由密度矩陣或稱密度算符表示，區分純態和混態的方法即可由此得之。純態S可用狄拉克符号的右括向量表示：

$S = | \Psi \rangle$ ，

或寫成密度矩陣表示型則為：

$S = \rho = | \Psi \rangle \langle \Psi |$ ；

而混態的密度矩陣則為

$S = \rho = \Sigma_i c_i | \Psi_i \rangle \langle \Psi_i |, \Sigma _i c_i = 1$ 。

就某種意義上來說，純態也可以說成是混態中的一項特例。只要將上式 $c_i \,$ 其中一項設為1， $c_i \,$ 其他項皆為0，則純態式子就可從混態式子中迸現出來。

區分純態與混態[编辑]

區分純態與混態的方法要利用到 $tr(\rho) \,$ 。 $tr(\rho) \,$ 表示對矩陣 $\rho \,$ 取對角線元素和(trace)，將純態和混態做歸一化動作，使得 $tr(\rho) \,$ 之值皆會是1。
而兩者不同處在於 $tr(\rho^2) \,$ ：歸一化過的純態 $tr(\rho^2)=tr(\rho)=1 \,$ ，而歸一化過的混態則 $tr(\rho^2)<1 \,$ ，和 $tr(\rho)=1 \,$ 不同，由此得以辨別出純態與混態。

舉例[编辑]

$\rho_1 = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{pmatrix}$ 為純態， $\rho_2 = \begin{pmatrix} \frac{1}{2} & 0 \\ 0 & \frac{1}{2} \end{pmatrix}$ 為混態

$\Rightarrow tr(\rho_1)=tr(\rho_2) = \frac{1}{2} + \frac{1}{2} = 1$

$\rho_1^2 = \rho_1 * \rho_1 = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{pmatrix}$ ； $\rho_2^2 = \rho_2 * \rho_2 = \begin{pmatrix} \frac{1}{4} & 0 \\ 0 & \frac{1}{4} \end{pmatrix}$ 。

$\Rightarrow tr(\rho_1^2)=tr(\rho_1) = \frac{1}{2} + \frac{1}{2} = 1$ ； $tr(\rho_2^2) = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} \ne tr(\rho_2) = 1$

量子脫散現象的過程中，與環境的交互作用會讓密度矩陣的非對角線元素(off-diagonal elements)隨時間衰減到0。也就是說在這個例子，隨著時間 $t \,$ 逐漸增加， 原本純態 $\rho_1 = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} e^{-\frac{t}{T_2}} \\ \frac{1}{2} e^{-\frac{t}{T_2}} & \frac{1}{2} \end{pmatrix} \Rightarrow \rho_1(t=0) = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{pmatrix}$
$\begin{matrix} {}^{t \rightarrow \infty} \\ \to \\ {} \\ {} \\ {} \\ {} \end{matrix}\quad \,$ 混態 $\rho_2 = \begin{pmatrix} \frac{1}{2} & 0 \\ 0 & \frac{1}{2} \end{pmatrix}$ 。

以混沌方式被激发，这就是我们所说的热光。而热态属于统计混合态，不能像描述纯态光场那样用态矢来描述热光场，因此我们采用密度算符来描述处于混和稳定态的热光场。按照密度算符理论，描述处于混合态的光场的密度算符定义为：

（2-12） iiiiPρψψΣ

式中 ——归一化的光场纯态态矢； iψ

——光场处于纯态的概率； iPiψ

描述多模热光场的密度算符可以写为：

（2-13） 1{}()(1)kkknkkknnkknnnnρ+=+ΣΠ

式中 ——是光场第k模的平均光子数kn

对于一个多模并存的热光场，由于其各个模式之间相互统计独立，其二阶关联度和一阶关联度满足下列关系：

（2-14） 2(2)(1)1()ggτ+

如果假设光源不是均匀加宽的，即光场具有高斯谱线型的分布，则有：

（2-15） 202()2212kkkneωωδωπδ−−∝

式中——对应的线宽参数δ

由多模热光场的密度算符公式（2-12）计算可得：

（2-16） 2()(1)2()()kikkkkkknegnωτωτω−=ΣΣ

根据公式（2-14），（2-15），（2-16），多模热光场的二阶关联度计算可得

phymath999