可数无穷大不可数无穷大都是一个方向的(一个正方向)。 而复数无穷大是全方位的,它有不可数无穷多个方向!就像平面上的零点的“邻域”里有无穷多个方向。
邻域是数学概念,这里指平面上一个点附近任意小的一个区域内的所有点。所以,有不可数无穷多个,而且还包括不可数无穷多个方向
走近量子纠缠-14-qubit和费曼
|
从上一节我们学到了,计算信息科学中的一个量子比特,可以对应于量子物理中一个粒子的叠加态。使用狄拉克的符号,单粒子叠加态(或量子比特)可以表示为:
|量子比特> = a|0> + b|1>, (14.1)
这里的a、b,是满足(|a|2+|b|2= 1)的任意复数,它们对应于两个定态在叠加态中所占的比例系数。当a=0,或者b=0时,叠加态就简化成两个定态|0>和|1>。两个比例系数的平方:|a|2或|b|2,分别代表测量时,测得粒子的状态是每个定态的几率。
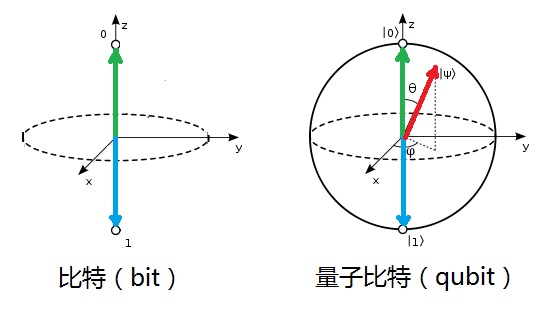
既然qubit是量子计算中的最基本的单元,我们对它稍微研究得更详细一点。下面图中是比特和量子比特的几何表示。图中绿矢和蓝矢,分别表示经典计算中所用的0和1两种状态。右边量子比特示意图中的红矢,表示量子世界中一个一般的叠加态,这些所有叠加态的端点,组成一个半径为1的单位球面,称之为Bloch球面。经典比特中的0和1也被包含在这个球面中。
表达式(14.1)中的比例系数a和b为复数,每个复数分别有一个实部,一个虚部,可以写成:
a = areal + aimagi , (14.2)
b = breal + bimagi , (14.3)
这儿的i = sqrt(-1),-1的平方根。
从(14.2)和(14.3)初看起来,以为一个量子比特具有4个任意常数(areal、aimag、breal、bimag),也就是说,有4个自由度。但实际上,一个量子比特只有2个自由度。其原因是因为在这4个任意常数之间,规定了如下2个约束:一是a、b需要满足几率归一化的条件:(|a|2+|b|2= 1)。二是两个复数a、b中,只有它们相对的相位差才有物理意义,量子叠加态的绝对相位是不可观测的,没有物理意义。因此,我们就干脆将a简化表示成一个实数,即cos(q/2)的形式,而a、b之间的相位差记为 f 。这样一来,两个自由度以两个实数角度q和f表示,(14.2)和(14.3)可写成:
a = cos(q/2), (14.4)
b = exp(if)sin(q/2), (14.5)
因此,一个qubit用叠加态来表示:
|量子比特> = |y> = a|1> + b|0>,
上式中的a、b由(14.4)和(14.5)所决定。不难看出,将量子比特态|y>在三维极坐标中表示出来,就是上面图中Bloch球面上的一个点。
综上所述,一个qubit有无穷多个状态,遍布整个球面。每个状态对应于Bloch单位球面上的一个点。在量子比特上进行一个运算,把qubit从一个状态变成另一个状态,或者说,将球面上的一个点变成另一个点。这种对应于布洛赫球面旋转的变换是一种幺正变换(Unitary Transformation)。所以,对qubit作一系列运算就相当于进行一连串的幺正变换。
从布洛赫球的图中还可以看到,经典计算机中的bit两个状态:|1> 和 |0>,也已经被包含在布洛赫球面中,分别对应于球面上南极和北极两个点。所以,我们可以说,经典比特是量子比特的特例。或者说,量子计算机是经典计算机的推广。
这个推广非同一般,从经典计算机推广到量子计算机,使得计算能力成指数倍地增长。
使用量子比特,与使用经典比特的另一個不同之处,是当我们有多于一個qubit连在一起時,能将它们互相关联起来,构成纠缠态。也就是说,经典计算机中,许多bit靠在一起组成寄存器时,每个bit独立坐在自己的座位上,互相不关联。而量子计算机里的qubit不但紧紧靠在一起,还手挽着手,显得分外亲热。当然,这些qubits是以何种方式,如何牵手的?是每两个qubits都牵着手呢,还是只是两个相邻的qubits才牵手?它们牵手的方式,对我们的计算及通讯,又有些什么不同的作用和意义?对这些问题,科学家们也是极为考究的。
再以上一节中提到过的三粒子GHZ纠缠态和W纠缠态为例说明。首先,我们将这两种纠缠态的表达式推广到n个qubit的情形。那时,它们可以写成:
|GHZ>n = |11…1> + |00…0> (14.6)
|W>n= |10…0> + |01…0> + … |00…1> (14.7)
上一节中我们还将GHZ纠缠态比喻为Borromean环,而将W纠缠态比喻为Hopf环。简言之,GHZ纠缠态是断开一个就全部断开,而W纠缠态却是断开一个不影响其余。对于n个qubit构成的GHZ态和W态,这个描述仍然适用。比如,拿W态来说吧,n个qubit构成的W纠缠态,在其中一个纠缠断开了的情况下,其余n-1个qubit还能继续保持互相纠缠。这个性质可以用到量子计算机的存储器上,以保证存储器在一个单元出了问题时,其余部分还有可能维持正常工作。GHZ纠缠态的性质在量子通讯中也有它的用武之地,它就像是有许多把锁,全部套在一起,锁住了一个共用的大房间,每个人都只需要打开自己的那把锁,房间就开了。这可以类似于所有的合伙人共用一套密码来传递信息的情况,大家都能用自己的钥匙打开房间,使用起来才比较方便。
量子计算机的最初设想,是美国物理学家理查德•费曼提出来的。我们在此文中,曾经多次提到费曼。费曼1918年生于纽约一个犹太人家庭。想必不少人都读过那几本颇为精采的、描写费曼趣事的自传性的小册子:《别闹了,费曼先生》和《你干吗在乎别人怎么想》等等。不同于一般理论物理学家在人们心目中的严谨刻板形象,费曼被人誉为“一个智慧超凡的科学鬼才”,其传奇故事脍炙人口。他从小就是个科学顽童,后来不仅是著名的物理学家,也是一位开保险箱专家和经常演出的邦戈鼓手。此外,他还曾经像一位真正的画家一样卖掉过自己的好几幅绘画作品。中学毕业后,他进入波士顿的麻省理工学院读大学本科,再后来到普林斯顿大学读Ph.D.,师从约翰·惠勒。刚从研究生毕业,他就参加了研制第一颗原子弹的著名曼哈顿计划。之后,他开创路径积分的想法,在量子场论中,用形象的费曼图,直观地表示粒子散射、反应和转化等过程。因为他对量子电动力学的杰出贡献,被授予1965年的诺贝尔物理学奖。
1981年的五月,美国波士顿MIT的校园里,鲜花盛开,绿草如茵。科学家们在这儿召开了物理学和计算机技术的第一次会议,费曼博士在会上作了一个“Simulating Physics With Computers”的报告,从此揭开了研究发展量子计算机的新篇章。

像许多科学家一样,费曼先生企图用计算的方式来模拟这个物理世界。他在报告中提出了一连串令人深思的问题。首要问题是:经典的图灵计算机可以用来模拟量子物理吗?答案是否定的,就像现在的经典计算机无法在足够短的时间内破解保密通讯的密码一样,当我们试图用计算机来模拟量子力学时,计算量将随着系统(微观粒子数)的增大而指数增加。那么,既然经典的计算机不行,是否有其他的计算模式可以模拟量子世界呢?费曼的想法别出一格,却又合情合理:他认为微观世界的本质是量子的,想要模拟它,就得用和自然界的工作原理一样的方式,也就是量子的方式才行。对此,费曼风趣地表示,既然这个该死的大自然不是经典的,你最好是“模拟它的方法来模拟它”,以其人之道,还治其人之身嘛!我们得做到和大自然做的一模一样。那就是说,我们要想模拟这个量子行为的世界,就得研究微观世界的量子是如何工作的,然后,建造一个按照量子力学的规律来运行的计算机,最后才能模拟它。不过,费曼最后又感叹地说:“天哪,这是一个非常精彩的问题,但却不是那么容易解决的!”
是可爱的费曼先生首先将物理学和计算机理论联系到一起,是他在MIT会上精彩的演讲,使得计算机科学家开始用热情的目光关注物理学的进展,关注量子力学。于是,这才有了后来种种有关“qubit”及其算法的研究,以及量子信息、量子计算、量子通讯、量子传输等等各个技术领域的重大发展和突破。
难能可贵的是,费曼还是一个孜孜不倦的物理教育家,他为大学生们所写的《费曼物理学讲义》,是由费曼的课上录音记录整理而成的,有趣的是,据说费曼真正去课堂上课时,每次只带一张纸!这三大册物理讲义,远远不同于一般的教科书,特别是书中融入了费曼的个人思维方式和对物理学的观点,至今仍然被视为大学物理教材中的经典。
理查德•费曼于1988年69岁时去世。一代奇才从此长眠地下,留给我们他对物理学,对计算机科学,对艺术,对生活的超凡理解和无限热忱。还有他在病床上逝世前的最后一句话,如今听起来,是否也颇有费曼先生活跃风趣的影子暗藏其中呢?费曼最后的话是:
“还好,人只需要死一次!否则很讨厌,因为它是如此地沉闷……”
别了,费曼先生!
No comments:
Post a Comment