自然底數 e 的定義 (上)
上周和 S 閒聊時 無意間聊到自然底數 e (又稱尤拉常數)
就我們從高中第一次接觸到他 一直到念了大學 大致上看到的定義有下面三種:
1. 定義下面數列的極限值為 e:
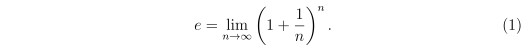
2. 我們先定義對數函數
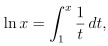
則自然對數 ln x 的底數, 我們就定義為 e. 即
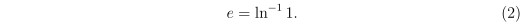
3. 定義指數函數
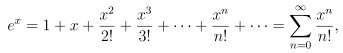
其中 0! = 1. 則 x = 1 代入可以得到

而我們兩個當天討論的重點在於
「這三種完全迥異的定義方式所定義出來的 e, 我們是怎麼肯定他們是 "相同" 的」
不過 這三個值相等 (或說這三個敘述是等價) 的證明 我們留到最後再說
第一個定義我是在高三的時候遇到 (這部分內容已在 88 年後的課綱已刪除)
去考慮這個數列

的極限是有他的背景和意義:
一來 納皮爾當初在粗創 "對數" 這個概念時 用的是以底數 b = 1 - 10^{-8} = 0.9999999 所形成的關係:
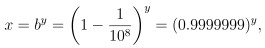
然後去計算對應到每一個整數 y 的值 x
或許你會覺得奇怪 怎麼會去考慮用這麼奇怪的數字 b 來做為底數
但如果你真的去計算 (用 Excel 就可以了) 你會發現所對應的 x 值的變化非常的小:
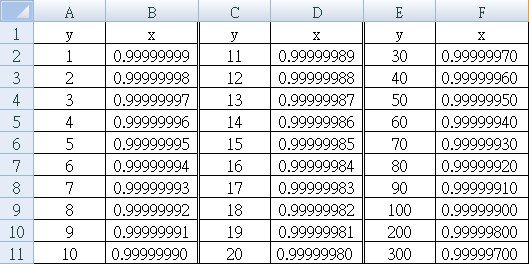
這樣的好處是 你不用擔心在對數表裡找不到你要的 x 而無法使用對數的性質來做計算
雖然納皮爾並不是用 e 來當作他的底數 但他所使用的 b 為後代的我們帶來啟發
更重要的是 為什麼我們會去討論以這個奇怪數列的極限值當作底數的對數 就其來有自了
第二個原因 是和銀行的計息有關-跟計算複利的期數有關
複利計息的意思是: 每次計息時是以戶頭裡 "所有的錢" 來計息利息 因此會利滾利
(另一種計息方式是單利 是指每次計息皆以 "存進去的錢" 來計算 之前生的利息不能再生息)
假設我們存入的本金為 A 元 年利率為 r 每年計息一次 則

以此類推 到第 t 年時 我們的本利和 S 就有
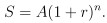
但並不是所有的銀行計算利息的方式都是一年一次
如果他一年計息兩次 則每次的利率即為年利率 r 除以 2 但半年就會記息一次
因此第 t 年就會記息 2t 次 所得到的本利和 S 即為
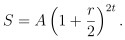
所以 如果一年計息 n 次 則每次的利率為 r/n 而且 t 年後的本利和 S 就是
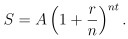
當然 身為顧客的我們 一定會問 到底分成幾期對我們是比較有利的
也就是去看當 n 越來越大時 數列
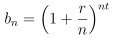
的值會是怎樣的變化
而數列 {b_n} 跟我們在第一個定義裡所使用的數列 {a_n} 類似 (當 r = 1, t = 1 兩者就是一樣了)
所以去討論 {a_n} 的極限是有他實際應用的地方
(因此我們知道 分太多期的意義不大 因為他會趨近一個定值 而不是無止盡的變大)
這三個定義中 第二個定義對我來說是比另外兩個還要 "自然" 的
我們是會去看一個數列的極限 也的確會去考慮一個無窮級數的和
但把這麼奇怪的數字拿來當作對數的底數 這怎麼想我也不會想去做這樣的事情
第二個定義幾乎是所有微積分課本對對數函數 ln x 以及自然底數 e 的定義方式
根據積分公式
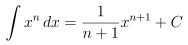
可以得到下表:
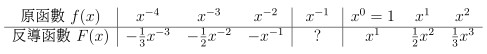
我們發現當 n = -1 代入積分公式時會時分母變成 0 無法使用積分公式
因此一切的關鍵就是想知道 "1/x 的積分會是誰" 或者是 "誰微分後會得到 1/x"
我們知道 對 1/x 積分的意思就是去看 y = 1 /x 下方的面積
因此 我們可以很肯定的知道 函數
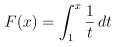
是存在的
但! 注意一件事!
到目前為止 我們無法得知 F(x) 會是一個對數函數! 這是需要檢查的!
只是 我很好奇第一個發現 F(x) 是對數函的人 是基於怎樣的觀察而去做下面的檢查
不論是以哪一個數為底數 只要符合下面兩個條件 他就是對數函數家族的一員:
(i) 對於任意的底數, log 1 都會等於 0
對我們來說 就是要去說 F(0) = 1
這是一個簡單的事 直接從定義就可以得到:
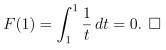
(ii) 對數律 log (ab) = log (a) + log (b) 要保持
對我們來說 就是要證 F(ab) = F(a) + F(b)
這就不容易了 證明如下:

O.K. 現在確定了 F(x) 是一個對數函數 因此我們把他記作 ln x
既然 F(x) = ln x 是一個對數函數 當然我們會問他是以哪一個數為底數的對數函數
這不是個簡單的問題 但有個簡單的解決方法
就是直接定義 ln x 的底數用符號 e 來表示 夠賤吧 XD
而這樣定義的好處 也出現在找指數函數 e^x 的微分上
(廢話 微積分課本裡用了一個不好找微分的方式來定義 e^x 這豈不是拿石頭砸自己的腳嗎?)
首先 因為 e 是對數函數 ln x 的底數 因此指數函數 e^x 和 ln x 互為反函數
又我們知道 ln x 是 1/x 積分的結果 所以反過來說 ln x 的微分就是 1/x
因此使用隱含數為分法 令 y = e^x 則
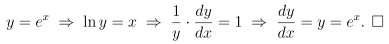
第三個定義出現在高等微積分課本
對一個第一次認識自然底數 e 的人而言
應該會覺得這個定義最莫名其妙 至少到目前為止 我還找不到一個自然說法讓 e 要這樣定義
再換個角度看 他其實也就只是指數函數 e^x 的泰勒展開式
但這個幂級數在數學的分析領域裡 卻是非常重要 也非常好用
舉個最經典的令子:
除了 e^x 是用幂級數表示外 我們也將正弦函數 sin x 與餘弦函數 cos x 用幂級數表示:
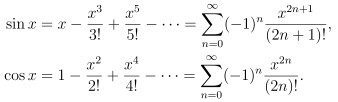
接著 我們把 x = iy 代入 得到
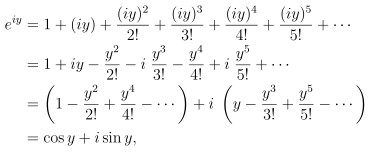
最後把 y = pi 代入 就會得到鼎鼎大名的 "尤拉公式":
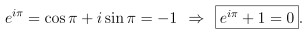
這個集合了 0, 1, i, e, pi 五個數學基本元素的公式
到現在還是決大多數數學家認為最美個數學公式
很神奇吧 他是這樣被發現的
而因為這些幂級數真的是太有用了 也比前兩個定義好用太多了
所以編書者常常為了節省時間 節省篇幅
就直接拿這個幂級數來當作 e^x 的定義
以減省從前兩個定義翻山過嶺才得到這個幂級數的過程 方便後面的發展
寫到這邊 赫然發現
我一開始所提的問題 現在連邊都還沒有勾上
只是再寫下去 對一篇網誌來說 我覺得太長了 (其實是自己累了 想休息了)
所以就敬請期待下集囉 ^^
就我們從高中第一次接觸到他 一直到念了大學 大致上看到的定義有下面三種:
1. 定義下面數列的極限值為 e:
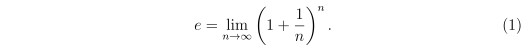
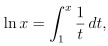
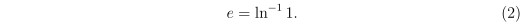
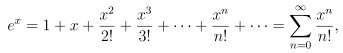

「這三種完全迥異的定義方式所定義出來的 e, 我們是怎麼肯定他們是 "相同" 的」
不過 這三個值相等 (或說這三個敘述是等價) 的證明 我們留到最後再說
第一個定義我是在高三的時候遇到 (這部分內容已在 88 年後的課綱已刪除)
去考慮這個數列

一來 納皮爾當初在粗創 "對數" 這個概念時 用的是以底數 b = 1 - 10^{-8} = 0.9999999 所形成的關係:
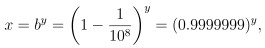
或許你會覺得奇怪 怎麼會去考慮用這麼奇怪的數字 b 來做為底數
但如果你真的去計算 (用 Excel 就可以了) 你會發現所對應的 x 值的變化非常的小:

雖然納皮爾並不是用 e 來當作他的底數 但他所使用的 b 為後代的我們帶來啟發
更重要的是 為什麼我們會去討論以這個奇怪數列的極限值當作底數的對數 就其來有自了
第二個原因 是和銀行的計息有關-跟計算複利的期數有關
複利計息的意思是: 每次計息時是以戶頭裡 "所有的錢" 來計息利息 因此會利滾利
(另一種計息方式是單利 是指每次計息皆以 "存進去的錢" 來計算 之前生的利息不能再生息)
假設我們存入的本金為 A 元 年利率為 r 每年計息一次 則

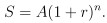
如果他一年計息兩次 則每次的利率即為年利率 r 除以 2 但半年就會記息一次
因此第 t 年就會記息 2t 次 所得到的本利和 S 即為
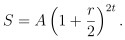
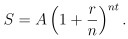
也就是去看當 n 越來越大時 數列
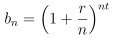
而數列 {b_n} 跟我們在第一個定義裡所使用的數列 {a_n} 類似 (當 r = 1, t = 1 兩者就是一樣了)
所以去討論 {a_n} 的極限是有他實際應用的地方
(因此我們知道 分太多期的意義不大 因為他會趨近一個定值 而不是無止盡的變大)
這三個定義中 第二個定義對我來說是比另外兩個還要 "自然" 的
我們是會去看一個數列的極限 也的確會去考慮一個無窮級數的和
但把這麼奇怪的數字拿來當作對數的底數 這怎麼想我也不會想去做這樣的事情
第二個定義幾乎是所有微積分課本對對數函數 ln x 以及自然底數 e 的定義方式
根據積分公式
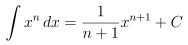
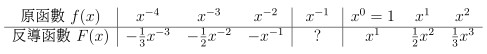
因此一切的關鍵就是想知道 "1/x 的積分會是誰" 或者是 "誰微分後會得到 1/x"
我們知道 對 1/x 積分的意思就是去看 y = 1 /x 下方的面積
因此 我們可以很肯定的知道 函數
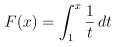
但! 注意一件事!
到目前為止 我們無法得知 F(x) 會是一個對數函數! 這是需要檢查的!
只是 我很好奇第一個發現 F(x) 是對數函的人 是基於怎樣的觀察而去做下面的檢查
不論是以哪一個數為底數 只要符合下面兩個條件 他就是對數函數家族的一員:
(i) 對於任意的底數, log 1 都會等於 0
對我們來說 就是要去說 F(0) = 1
這是一個簡單的事 直接從定義就可以得到:
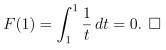
對我們來說 就是要證 F(ab) = F(a) + F(b)
這就不容易了 證明如下:

既然 F(x) = ln x 是一個對數函數 當然我們會問他是以哪一個數為底數的對數函數
這不是個簡單的問題 但有個簡單的解決方法
就是直接定義 ln x 的底數用符號 e 來表示 夠賤吧 XD
而這樣定義的好處 也出現在找指數函數 e^x 的微分上
(廢話 微積分課本裡用了一個不好找微分的方式來定義 e^x 這豈不是拿石頭砸自己的腳嗎?)
首先 因為 e 是對數函數 ln x 的底數 因此指數函數 e^x 和 ln x 互為反函數
又我們知道 ln x 是 1/x 積分的結果 所以反過來說 ln x 的微分就是 1/x
因此使用隱含數為分法 令 y = e^x 則
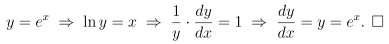
第三個定義出現在高等微積分課本
對一個第一次認識自然底數 e 的人而言
應該會覺得這個定義最莫名其妙 至少到目前為止 我還找不到一個自然說法讓 e 要這樣定義
再換個角度看 他其實也就只是指數函數 e^x 的泰勒展開式
但這個幂級數在數學的分析領域裡 卻是非常重要 也非常好用
舉個最經典的令子:
除了 e^x 是用幂級數表示外 我們也將正弦函數 sin x 與餘弦函數 cos x 用幂級數表示:
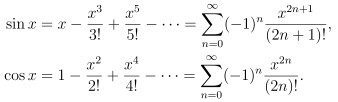
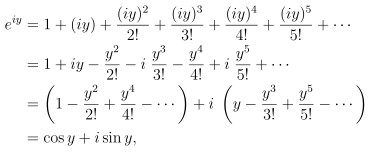
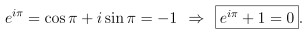
到現在還是決大多數數學家認為最美個數學公式
很神奇吧 他是這樣被發現的
而因為這些幂級數真的是太有用了 也比前兩個定義好用太多了
所以編書者常常為了節省時間 節省篇幅
就直接拿這個幂級數來當作 e^x 的定義
以減省從前兩個定義翻山過嶺才得到這個幂級數的過程 方便後面的發展
寫到這邊 赫然發現
我一開始所提的問題 現在連邊都還沒有勾上
只是再寫下去 對一篇網誌來說 我覺得太長了 (其實是自己累了 想休息了)
所以就敬請期待下集囉 ^^




No comments:
Post a Comment