math01 我是e的x次方 ex不論對x微分幾次，結果都還是ex，

自然對數的底數e

台灣師大數學系二年級 趙國亨

滄海桑田世事非 始終不變未曾悔

高中教師常常用這麼一則笑話，幫助學生記憶一個很特別的微分公式，故事是這麼說的：

在一家精神病院裡，有個病患整天對著別人說，「我微分你我微分你」，也不知為什麼，這些病患都有一點簡單的微積分概念，總以為有一天自己會像一般多項式函數般，被微分到變成零而消失，因此對他避之唯恐不及，然而某天他卻遇上了一個始終不為所動的人，他很意外地問他為何不會害怕，這個人淡淡地對他說，「我是e的x次方。」

這個微分公式就是：e^x不論對x微分幾次，結果都還是e^x，一絲不變！難怪數學系的學生會用e^x，來比喻堅定不移的愛情！

熟悉數學的人都知道，在π之後，第二個最重要的數學常數是e。但是不同於π的歷史輝煌，它擁有「由π的準確位數可以看出一個文明當時的數學水準，甚至是文化水準」這般地位，自然對數的底數e的出現幾乎不可考，我們僅知道人們發現數列 (1+1/n)ⁿ在n趨近於 ∞ 時，會趨近於一個常數。這個數列是由於金融業的發達，為了處理複利的計息週期而出現，然後這個常數的估計值，則要等到對數出現後，才能被真實地評定。

對數函數無所假 天文學家延生涯

十七世紀初，蘇格蘭數學家John Napier『發明』了對數 (logarithm)。其實，筆者也不知道該不該稱呼Napier為數學家，畢竟他是個對宗教狂熱、具有機械天份、喜歡用鬼點子解決問題的有趣貴族。更讓人意外的，是他居然紮實地做了廿年的苦工，完成了史上第一張對數表。

與我們現在所熟知的對數不同，這張對數表的底數是1-10^-7而不是10，以10為底的常用對數在Briggs與Napier見面之後，才在Briggs的手中誕生。可敬的Napier在做出對數表的三年後，便與世長辭，而這門不假其他數學研究的學問，才正要席捲數學界。在此，容我用西北雨來形容對數這項發明的出現：

埋首計算那煩悶一如夏日午後的龐大乘法，毫無預兆地幾滴名為「對數」的斗大雨滴落下，轉眼整個數學界的天空變了顏色，狂洩的雨水淋濕了厚重的計算紙，雨過天青，計算紙上繁複的乘法變成加法，簡單一如雨後的清爽空氣。雨後，天文學家，減少了計算時間，延長了學術生涯。

充斥於天地萬物 閃爍在晨曦蛛網

在一片空曠的草地上，有甲、乙、丙、丁、四隻狗，分別站立在一個正方形的四個頂點 A、B、C、D上。狗主人要甲狗緊盯著乙狗、乙狗緊盯著丙狗、丙狗緊盯著丁狗、丁狗緊盯著甲狗。一聲令下，四隻狗以相同的速度，同時衝向目標。假定每隻狗在每個時刻，都是正面朝向它的目標，那麼，這四隻狗所跑過的路徑是什麼形式呢？

上述題目出自趙文敏老師的文章〈等角螺線及其他〉，有興趣的人可以參考下列網站：http://episte.math.ntu.edu.tw/articles/sm/sm_20_09_1/index.html。他的答案是等角螺線，如果用極座標表示，等角螺線的基本形式就是r = ae^{θ cotθ}。

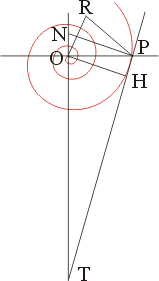等角螺線有著驚人的美妙相似性質，大自然中許許多多的生物身上，都顯示等角螺線的存在，鸚鵡螺的截面線條、鳳梨、向日葵的螺旋紋，都是這種形式。另一方面，等角螺線在數學上，也有許多神奇的性質，如右圖中，做一過P點的切線截y軸於T點，則從O點沿著螺線到P點的距離恰好等於PT的距離，這是由伽利略 (Galileo Galilei)的學生托里切利 (Torricelli) 證明出來。

另一方面，有個經常被誤認為是拋物線的曲線，也跟e分不開來，它被稱為懸鏈線，源自開始大量使用極座標研究螺線的Jakob Bernoulli提出來的問題：「把一條細繩掛在兩定點上，讓他自由懸垂下來，求：這細繩會構成怎樣的曲線。」這個曲線的基本形式是( e^x + e^x ) / 2，同時，它也是相同條件下位能最小的曲線。當然，這個答案在當時不是這個樣子的，因為要等到尤拉 (Euler) 來為自然對數命名。

隨手拈遊戲之作 遺我以美麗結果

相對於π是希臘文字中圓周的第一個字母，e是由來的是較不為人所熟知的。一般咸認為尤拉是建議將e作為自然對數的底數之數學家，因此，偶爾總會有人認為：根本就是尤拉 (Euler) 取自己名字的第一個字母作為自然對數。但是，別忘了大家稱呼e為自然對數的底數，而不是Euler對數或Euler常數 (注1)。

尤拉選擇e的理由較為人所接受的說法有二：一為在a, b, c, d等四個常被使用的字母後面，第一個尚未被經常使用的字母就是e，所以，他很自然地、毫不避嫌地選了e這個符號，代表自然對數的底數；一為e是指數 (exponential) 的第一個字母，雖然你或許會懷疑瑞士人尤拉 (Euler) 的母語又不是英文，很不幸地法文、德文的指數都是exponential (注2)。

不論如何，我們已經接受e代表著自然對數，現在，讓我們先拋開折磨人的嚴謹性，一起來感受一下Newton與Leibniz創造微積分之後，屬於數學界的大航海時代精神：

1. 首先大家都知道 e^x = 1 + x + x²/2! + x³/3! + x⁴/4! + x⁵/5! + …

2. 用 ix 代替 x

3. e^ix = 1 + ix + (ix)²/2! + (ix)³/3! + (ix)⁴/4! + (ix)⁵/5! + …
= 1 + ix - x²/2! - ix³/3! + x⁴/4! + ix⁵/5! + …
= ( 1 - x²/2! + x⁴/4! + … ) + i( x - x³/3! + x⁵/5! + … )
= cos x + i sin x (注3)

4. 如果你寫下另一個用 –ix 代替 x 的式子，就可以加減得到Euler三角函數公式 cos x = ( e^ix + e^-ix ) / 2 、 sin x = ( e^ix - e^-ix ) / 2i

5. 如果你將π代入 x ，就會看到 e^iπ = -1，也就是e^iπ + 1 = 0

感謝Lagrange、Cauchy、Weierstrass等等後來許多數學家們的努力，Euler的『遊戲之作』，在今日已經成了人們眼中最美麗的數學式！至於這個過程的『嚴謹性』，就讓大家等著看他怎麼出現在數學系的分析學課程之中了！

寫在最後…

很遺憾地刪掉了很多東西，像是許多可以讓文章更加生動的圖片、提到等角螺線就讓人自然而然聯想到的黃金比例及Fibonacci數列、e身為一個超越數對數學界的影響等等，但這是很難得的經驗。看了很多書，也學到很多過去沒注意的知識，很累、但很有充實感。

註解

1. 事實上Euler常數g 是另一個跟對數有關的常數。

2. 不過，筆者在懷疑會不會是l這個對數的開頭字母的書寫體壓扁的結果？畢竟l常常拿來代表長度，所以要將它變體一下囉~~

3. 在Euler之前，有一位英國數學家Roger Cotes計算出那個常數是2.7182818，同時，再提出以那個常數作為底數，得到if = log(cosf + isinf) ，其中 i = (-1)^1/2 。

參考書目：

American Council of Learned Societies (1991). Biographical Dictionary of Mathematicians. New York：Scribner。

Eli Maor (2000)，《毛起來說e》，鄭惟厚譯，台北：天下文化。

Ian Stewart (2000)，《大自然的數學遊戲》，葉李華譯，台北：天下文化。

Ian Stewart (2000)，《生物世界的數學遊戲》，蔡信行譯，台北：天下文化。

吳文俊等編 (1995)，《世界著名數學家傳記》，北京：科學出版社。

曹亮吉 (1996)，《阿草的葫蘆》，台北：遠哲科學教育基金會。

趙文敏撰，〈等角螺線及其他〉，《科學月刊》第二十卷，第九、十期。