 維基態能階是一維基態能階的
維基態能階是一維基態能階的  倍。只有一點不同,在一維案例裏,每一個能階對應於一個單獨的量子態。在
倍。只有一點不同,在一維案例裏,每一個能階對應於一個單獨的量子態。在  維案例裏,除了底態能階以外,每一個能階都是簡併的,都對應於多個量子態
維案例裏,除了底態能階以外,每一個能階都是簡併的,都對應於多個量子態量子諧振子
维基百科,自由的百科全书
目录[隐藏] |
[编辑] 一維諧振子
[编辑] 哈密頓算符與能量本徵態
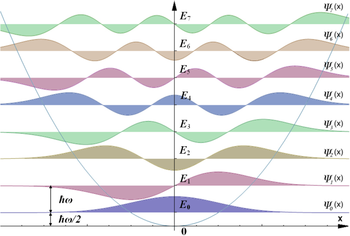
能量最低的六個束縛本徵態的波函數表徵 (n = 0 到 7)。橫軸表示位置 x 。此圖未經歸一化。
 。此粒子的哈密頓算符為
。此粒子的哈密頓算符為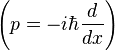 。第一項代表粒子動能,而第二項代表粒子處在其中的位能。為了要找到能階以相對應的能量本徵態,我們必須解所謂的「定态薛丁格方程式」:
。第一項代表粒子動能,而第二項代表粒子處在其中的位能。為了要找到能階以相對應的能量本徵態,我們必須解所謂的「定态薛丁格方程式」: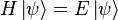 .
.
 為厄米多項式 (Hermite polynomials):
為厄米多項式 (Hermite polynomials): 。
。
 乘以1/2, 3/2, 5/2……等等。這是許多量子力學系統的特徵。在爾後的「階梯算符」段落,我們將對此現象做更詳細的檢視。再者,可有的最低能量(當 n = 0 )不為零,而是
乘以1/2, 3/2, 5/2……等等。這是許多量子力學系統的特徵。在爾後的「階梯算符」段落,我們將對此現象做更詳細的檢視。再者,可有的最低能量(當 n = 0 )不為零,而是  ,被稱為「基態能量」或零點能量。在基態中,根據量子力學,一振子執行所謂的「零振動」(null oscillations) 且其平均動能是正值。這樣的現象意義重大但並不那麼顯而易見,因為通常能量的零點並非一個有意義的物理量,因為可以任意選擇;有意義的是能量差。雖然如此,基態能量有許多的意涵,特別是在量子重力。最後一個理由式能階值是等距的,不像波耳模型或盒中粒子問題那樣。
,被稱為「基態能量」或零點能量。在基態中,根據量子力學,一振子執行所謂的「零振動」(null oscillations) 且其平均動能是正值。這樣的現象意義重大但並不那麼顯而易見,因為通常能量的零點並非一個有意義的物理量,因為可以任意選擇;有意義的是能量差。雖然如此,基態能量有許多的意涵,特別是在量子重力。最後一個理由式能階值是等距的,不像波耳模型或盒中粒子問題那樣。注意到基態的機率密度集中在原點。這表示粒子多數時間處在勢阱的底部,合乎對於一幾乎不帶能量之狀態的預期。當能量增加時,機率密度變成集中在「古典轉向點」(classical turning points),其中狀態能量等同於勢能。這樣的結果與古典諧振子相一致;古典的描述下,粒子多數時間處在(而更有機會被發現在)轉向點,因為在此處粒子速度最慢。因此滿足對應原理。
[编辑] 階梯算符方法
前述的冪級數解雖然直觀,但顯得相當繁複。階梯算符方法起自保羅·狄拉克,允許我們能抽得能量本徵值,而不用直接解微分方程式。此外,此法很容易推廣到更複雜的問題,尤其是在量子場論中。跟從此方法,我們定義算符 a 與其伴隨算符 (adjoint) a† :算符 a 與 a† 有如下性質:
![\left[x , p \right] = i\hbar](http://upload.wikimedia.org/math/d/f/7/df7973e6171425615a6dd3324219dae3.png) .
.
![\left[A , B \right] \ \stackrel{\mathrm{def}}{=}\ AB - BA](http://upload.wikimedia.org/math/1/9/f/19f2d27a3ee5732fe3e8e4bc669673dd.png) .
.

![\left[a , a^{\dagger} \right] = 1](http://upload.wikimedia.org/math/c/4/9/c49909cd4984a38a85dc95e3349a547d.png) .
.
 代表帶有能量 E 的能量本徵態。任何右括向量 (ket) 與自身的內積必須是非負值,因此
代表帶有能量 E 的能量本徵態。任何右括向量 (ket) 與自身的內積必須是非負值,因此 。
。
 ,
,
 。注意到當 (
。注意到當 ( ) 為零右括向量(亦即:長度為零的右括向量),則不等式飽和而
) 為零右括向量(亦即:長度為零的右括向量),則不等式飽和而 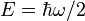 。很直觀地,可以檢查到存在有一狀態滿足此條件——前面段落所提到的基態 (n = 0)。
。很直觀地,可以檢查到存在有一狀態滿足此條件——前面段落所提到的基態 (n = 0)。利用上面等式,我們可以指出 a 及 a† 與 H 的對易關係:
![\begin{matrix}
\left[H , a \right] &=& - \hbar \omega a \\
\left[H , a ^\dagger\right] &=& \hbar \omega a^\dagger
\end{matrix}](http://upload.wikimedia.org/math/b/0/2/b02ba8ca67fe7c23bd93a50e8f3d43e5.png) .
.
 ) 並非零右括向量,
) 並非零右括向量,![\begin{matrix}
H (a \left| \psi_E \right\rangle)
&=& (\left[H,a\right] + a H) \left|\psi_E\right\rangle \\
&=& (- \hbar\omega a + a E) \left|\psi_E\right\rangle \\
&=& (E - \hbar\omega) (a\left|\psi_E\right\rangle)
\end{matrix}](http://upload.wikimedia.org/math/6/7/3/673fd0f8120bddb00955615aa2c46680.png) .
.
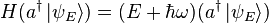 .
.
 的本徵態,而 a† 作用在能量為 E 的本徵態,產生出另一個能量為
的本徵態,而 a† 作用在能量為 E 的本徵態,產生出另一個能量為  的本徵態。因為這樣,a 稱作降算符而 a† 稱作升算符。兩者合稱階梯算符。在量子場論中,a 與 a† 也分別稱作消滅算符與創生算符,以其分別摧毀與創造粒子——對應於我們的能量量子。
的本徵態。因為這樣,a 稱作降算符而 a† 稱作升算符。兩者合稱階梯算符。在量子場論中,a 與 a† 也分別稱作消滅算符與創生算符,以其分別摧毀與創造粒子——對應於我們的能量量子。給定任何能量本徵態,我們可以拿降算符 a 作用在其上,產生了另一個能量少了
 的本徵態。重複使用降算符,似乎我們可以產生能量本徵態其能量低到 E = −∞ 。不過這樣就就與早先的要求
的本徵態。重複使用降算符,似乎我們可以產生能量本徵態其能量低到 E = −∞ 。不過這樣就就與早先的要求  相違背。因此,必須有一最底的能量本徵態——基態,我們標示作
相違背。因此,必須有一最底的能量本徵態——基態,我們標示作  (勿與零右括向量混淆),使得
(勿與零右括向量混淆),使得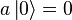 (即 a 對
(即 a 對  作用後產生零右括向量 (zero ket))。
作用後產生零右括向量 (zero ket))。
 。
。
 上,並且乘上適當的歸一化因子,可以產生出一個能量本徵態的無限集合
上,並且乘上適當的歸一化因子,可以產生出一個能量本徵態的無限集合  使得
使得 ,
,
這方法也能夠用來很快地找到量子諧振子的基態波函數。只要將消滅算符作用於基態,
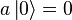 變為
變為 。
。
 。
。
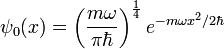 。
。
[编辑] 自然長度與能量尺度
量子諧振子擁有自然長度與自然能量兩個自然尺度,可以用來簡化問題。這可以透過無因次化來得到。結果是如果我們以 為單位來測量能量,以及
為單位來測量能量,以及 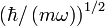 為單位來測量距離,則薛丁格方程式變成:
為單位來測量距離,則薛丁格方程式變成: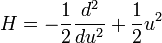 ,
,
 .
.
[编辑] 案例:雙原子分子
在雙原子分子中,自然頻率可以發現為[1]:
[编辑]  維諧振子
維諧振子
一維諧振子很容易地推廣到  維。在一維中,粒子的位置是由單一座標 x 來指定的。在
維。在一維中,粒子的位置是由單一座標 x 來指定的。在  維中,這由
維中,這由  個位置座標所取代,我們以
個位置座標所取代,我們以 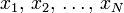 標示。對應每個位置座標有個動量,我們標示為p1, ..., pN。這些算符之間的正則對易關係為
標示。對應每個位置座標有個動量,我們標示為p1, ..., pN。這些算符之間的正則對易關係為![\begin{matrix}
\left[x_i , p_j \right] &=& i\hbar\delta_{i,j} \\
\left[x_i , x_j \right] &=& 0 \\
\left[p_i , p_j \right] &=& 0
\end{matrix}](http://upload.wikimedia.org/math/1/a/0/1a0fb98f21003d33bc6ba6cb0d3e9246.png) .
.
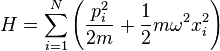 。
。
 維諧振子明確地可比擬為
維諧振子明確地可比擬為  個質量相同,彈性常數相同,獨立的一維諧振子。在這案例裏,變數
個質量相同,彈性常數相同,獨立的一維諧振子。在這案例裏,變數 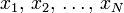 是
是  個粒子的位置坐標。這是反平方連心位勢的一個優良的特性,允許位勢被分離為
個粒子的位置坐標。這是反平方連心位勢的一個優良的特性,允許位勢被分離為  個項目,每一個項目只相依於一個位置坐標。
個項目,每一個項目只相依於一個位置坐標。這觀察使得問題的解答變的相當簡單。對於一個集合的量子數
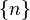 ,一個
,一個  維諧振子的能量本徵函數
維諧振子的能量本徵函數  等於
等於  個一維本徵函數
個一維本徵函數  的乘積:
的乘積: 。
。
 組階梯算符,
組階梯算符, ,
,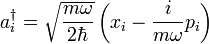 。
。
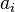 與
與  算符將能量分別降低或升高
算符將能量分別降低或升高  。哈密頓量是
。哈密頓量是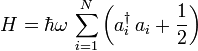 。
。
 是
是![E = \hbar \omega \left[(n_1 + \cdots + n_N) + {N\over 2}\right]](http://upload.wikimedia.org/math/3/1/c/31c13fe44d74f8b03561bb74fb57419c.png) ;
;
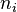 是
是  的量子數。
的量子數。如同一維案例,能量是量子化的。
 維基態能階是一維基態能階的
維基態能階是一維基態能階的  倍。只有一點不同,在一維案例裏,每一個能階對應於一個單獨的量子態。在
倍。只有一點不同,在一維案例裏,每一個能階對應於一個單獨的量子態。在  維案例裏,除了底態能階以外,每一個能階都是簡併的,都對應於多個量子態。
維案例裏,除了底態能階以外,每一個能階都是簡併的,都對應於多個量子態。簡併度可以很容易地計算出來。例如,思考三維案例,設定
 。每一個
。每一個  相同的量子態,都會擁有相同的能量。給予
相同的量子態,都會擁有相同的能量。給予  ,我們首先選擇一個
,我們首先選擇一個 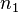 。那麼,
。那麼, ,我們有
,我們有  個值,從
個值,從  到
到 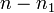 ,可以選擇為
,可以選擇為 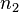 的值。
的值。 的值自動的設定為
的值自動的設定為  。因此,簡併度是
。因此,簡併度是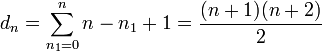 。
。
 維案例,
維案例, 。
。
[编辑] 案例:三維均向諧振子
- 參閱三維均向諧振子
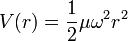 ;
;
 是這問題的質量。由於
是這問題的質量。由於  會被用來標記磁量子數,所以,用
會被用來標記磁量子數,所以,用  來標記質量。
來標記質量。這問題的薛丁格方程式為
 。
。
 ;
;
能量本徵值是
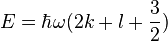 。
。
 來描述:
來描述: 。
。
 是個正整數,假若
是個正整數,假若  是偶數,那麼,角量子數也是偶數:
是偶數,那麼,角量子數也是偶數: ;
;
 是奇數,那麼,角量子數也是奇數:
是奇數,那麼,角量子數也是奇數: 。
。
 滿足不等式
滿足不等式 。
。
 與
與 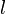 ,存在
,存在  個不同的量子態。每一個量子態都有不同的磁量子數
個不同的量子態。每一個量子態都有不同的磁量子數  。因此,
。因此, 的兼併度是
的兼併度是 ;
;
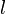 的初始值是
的初始值是  。 這結果與先前的方程式相同。
。 這結果與先前的方程式相同。[编辑] 耦合諧振子
設想 個相同質量的質點,以彈簧連結為一條一維的線形鏈條。標記每一個質點的離開其平衡點的位置為
個相同質量的質點,以彈簧連結為一條一維的線形鏈條。標記每一個質點的離開其平衡點的位置為 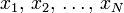 (也就是說,假若一個質點
(也就是說,假若一個質點  位於其平衡點,則
位於其平衡點,則  )。整個系統的哈密頓量是
)。整個系統的哈密頓量是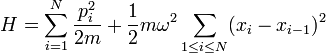 ;
;
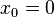 。
。很奇妙地,這個問題可以用坐標變換來變換成一組獨立的諧振子,每一個獨立的諧振子對應於一個獨特的晶格集體波震動。這些波震動表現出類似粒子般的性質,稱為聲子。許多固體的離子晶格都會產生聲子。在固體物理學裏,這方面的理論對於許多現象的研究與了解是非常重要的。
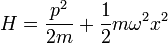




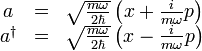

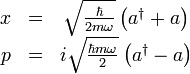

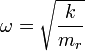
 為角頻率,
為角頻率, 是
是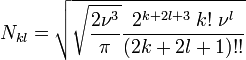 是歸一常數,
是歸一常數,
 是
是  是
是 是
是
No comments:
Post a Comment